
Уравнения математической физики. Пашуева И.М., Ускова Н.Б
.pdfМИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ
Федеральное государственное бюджетное образовательное учреждение высшего образования «Воронежский государственный технический университет»
И. М. Пашуева, Н. Б. Ускова, А. Н. Шелковой
УРАВНЕНИЯ МАТЕМАТИЧЕСКОЙ ФИЗИКИ
Учебное пособие
Воронеж 2020
1
УДК 512.64 ББК 22.143
П225
Рецензенты:
кафедра системного анализа и управления Воронежского государственного университета
(зав. каферой д-р физ.-мат. наук, проф. В. Г. Задорожний); канд. физ.-мат. наук, доц. Г. В. Гаркавенко
Пашуева, И. М.
Уравнения математической физики: учебное пособие
[Электронный ресурс]. – Электрон. текстовые и граф. данные П225 (2,1 Мб) / И. М. Пашуева, Н. Б. Ускова, А. Н. Шелковой. – Воронеж: ФГБОУ ВО «Воронежский государственный технический университет», 2020. – 1 электрон. опт. диск (CD-ROM):
цв. – Систем. требования: ПК 500 и выше; 256 Мб ОЗУ; Windows XP; SVGA с разрешением 1024x768; Adobe Acrobat; CD-ROM;
мышь. – Загл. с экрана.
ISBN 978-5-7731-0873-3
В учебном пособии содержатся элементы теории уравнений в частных производных.
Издание предназначено для студентов специальности 11.05.01 «Радиоэлектронные системы и комплексы» (специализация «Радиоэлектронные системы передачи информации») при изучении дисциплины «Математика» и направления 28.03.01 «Нанотехнологии и микросистемная техника» (профиль «Компоненты микро- и наносистемной техники)» при изучении дисциплины «Спецглавы математики» 2 и 3 курсов очной формы обучения.
Ил. 8. Библиогр.: 23 назв.
УДК 512.64 ББК 22.143
Издается по решению редакционно-издательского совета Воронежского государственного технического университета
ISBN 978-5-7731-0873-3 |
Пашуева И. М., Ускова Н. Б., |
|
Шелковой А. Н., 2020 |
|
ФГБОУ ВО «Воронежский |
|
государственный технический |
|
университет», 2020 |
|
2 |
ВВЕДЕНИЕ
Это учебное пособие написано на основе лекций, читаемых на факультете радиотехники и электроники ВГТУ по курсу «Математика».
В пособии изложены необходимые основы математического аппарата и примеры его использования в современных физико-технических приложениях: элементы теории уравнений в частных производных, математической физики. Такой объѐм знаний актуален сегодня для студентов, получающих образование по радитехническим специальностям, и соответствует требованиям государственных стандартов по информационным специальностям.
Изложение материала проведено почти без доказательств – основной упор сделан на приобретение навыков использования математического аппарата. Каждый раздел сопровождается решением характерных задач и соответствующими физико-техническими приложениями. Пособие также содержит подборку вопросов для повторения, задач и упражнений для самостоятельного решения по каждой теме.
3
ГЛАВА 1. ПРИМЕРЫ ОСНОВНЫХ УРАВНЕНИЙ МАТЕМАТИЧЕСКОЙ ФИЗИКИ
Математическая физика представляет собой науку о математическом моделировании проблем, возникающих в физике. Многие задачи из разных разделов физики описываются дифференциальными уравнениями в частных производных, являющимися соотношениями между функцией u, ко-
торую нужно найти, еѐ частными производными различных порядков и независимыми аргументами. Исходя из таких соображений в прикладных вопросах дифференциальные уравнения в частных производных называются уравнениями математической физики. Приведѐм несколько примеров таких уравнений.
1.1. Уравнение колебаний
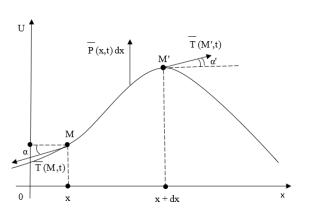
Уравнение колебаний струны.
Рассмотрим натянутую струну, то есть тонкую, упру-
гую нить, находящуюся в плоскости
Oxu,
эта нить под воз-
действием некоторого возмущения, о котором мы знаем, от-
клонилась от своего равновесного положения
Ox.
Исследуем
еѐ поперечные колебания, имя в виду, что при данном колебании струны еѐ точки перемещаются в направлении, перпендикулярном оси Ox.
Пусть u u x, t – сдвиг точки струны с абсциссой x в
момент времени t относительно Ox |
(рис. 1). |
В этом случае функция u x, t |
при 0 t моделирует |
процесс колебаний струны: для всякого фиксированного мо-
4
мента времени |
t t |
зависимостью |
1 |
мгновенный профиль струны.
u u x, t1 описывается
Рис. 1. Отклонение точки струны от положения равновесия
Дальнейшее изложение будем осуществлять при наличии нижеописанных предположений.
1. Условимся, что в струне имеют место малые колебания, то есть вид струны под воздействием колебаний почти
такой же, как прямая u 0. |
При этом считаем, что тангенс |
|
угла наклона касательной |
к графику функции |
u x, t , |
t const,
величине
то есть |
tg |
u |
, |
|
x |
||||
|
|
|
по сравнению
бесконечно мал по абсолютной
с единицей. Таким образом,
sin tg и cos 1.
5

2. В концах всякого элемента дуги |
MM |
|
струны дей- |
|
ствуют направленные по касательной упругие силы натяже-
ния (рис. |
1) с одинаковыми абсолютными значениями |
||||||
|
|
|
|
|
|
|
|
T M , t |
|
|
и являющимися в действительно- |
||||
T M , t T0 |
|||||||
сти константами, то есть |
T0 |
перманентна при изменении x и |
|||||
t. |
|
|
|
|
|
||
|
|
3. Имеет место воздействие на струну непрерывно рас- |
|||||
пределѐнных сторонних силы в направлениях, перпендику-
лярным оси Ox, с плотностью (нагрузкой) |
p x, t |
в рассчѐте |
||
на единицу длины. |
|
|
|
|
Удалим из струны бесконечно малый участок дуги |
MM |
|
||
|
||||
с абсциссами его концов x и x dx. Вместо действия удалѐнных левой и правой частей струны будем рассматривать соответствующие силы натяжения. В этом случае участок ду-
ги MM |
|
имеет смысл интерпрерировать как свободную мате- |
|||
|
|||||
риальную |
точку, на которую воздействуют упругие |
силы |
|||
T M , t |
, |
|
где |
eu – |
|
T M , t и сторонняя сила p x, t dx eu , |
|||||
орт оси Ou. |
|
|
|||
Обозначим через x линейную плотность |
струны в |
||||
точке x. |
Поскольку в равновесном положении масса элемен- |
||||
та равна x dx, то, в силу сохранения массы, участок дуги
MM обладает такой же массой. Пусть и – углы наклона к оси Ox касательных к профилю струны в момент времени t соответственно в точках M и M . Производя проекции
6

на ось
Ou
сил, действующих на участок дуги
MM ,
на осно-
вании закона Ньютона и допущения 2), будем иметь
|
|
u |
|
|
|
|
|
|
|
|
|
|
x dx |
2 |
|
T sin T sin p x, t dx. |
|
|
|||||||
|
|
1 |
||||||||||
|
t |
2 |
0 |
0 |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
На основании допущения 1) углы |
|
и |
|
|
бесконечно |
|||||||
|
||||||||||||
малы; таким образом |
|
|
|
|
|
|
|
|
|
|||
|
|
|
sin tg u |
|
|
|
|
|
2 |
|
||
|
|
|
|
x |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
||
и |
|
|
|
|
|
|
|
|
|
|
|
|
|
sin tg |
u |
|
. |
|
|
|
|
|
|
||
|
x |
x dx |
|
|
|
|
2 |
|
||||
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
Для вычисления
2 |
|
|
|
будем рассматривать известную форму-
лу математического анализа
f x dx f x f x dx,
справедливую с точностью до бесконечно малых высших порядков. Отсюда имеем:
sin |
|
u |
|
2u |
dx. |
|||||||
x |
x2 |
|||||||||||
|
|
|
|
|
|
|
|
|||||
Подставляя выражения |
|
2 |
и 3 в 1 , |
|||||||||
|
|
u |
|
|
|
u |
|
|
||||
x |
2 |
|
|
|
|
|
2 |
|
|
p x, t |
||
|
2 |
|
T |
|
|
|
2 |
|||||
|
t |
|
|
0 |
x |
|
|
|||||
|
|
|
|
|
|
|
|
|||||
будем иметь
.
3
4
Таким образом, имеет место уравнение малых вынужденных поперечных колебаний струны.
7

Когда плотность является константой ( x – постоян-
ная величина) данное уравнение преобразуется к форме
в которой
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
t |
|
a |
2 |
|
T |
, |
|
0 |
|||||
|
|
|
|||
|
|
|
|
|
u |
a |
|
|
|
2 |
2 |
|
|
P |
p |
|
|
||
|
u |
|
2 |
|
|
x |
|
|
|
2 |
|
x, t
P x, t , |
5 |
|
– плотность силы в расчѐте на
единицу массы. |
|
Когда нет сторонней силы |
P x, t 0 , |
уравнение малых свободных колебаний струны:
имеет место
|
|
u |
|
|
|
|
u |
|
|
|
|
|
2 |
|
a |
|
2 |
|
|
. |
|
|
|
|
|
|
2 |
|
|
|
6 |
|
|||
|
t |
2 |
|
|
|
x |
2 |
|
|||
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
||
Уравнения вида |
4 |
- |
6 |
описывают не только колеба- |
|||||||
ния струны, но и ряд других физических процессов, которые называются волновыми. Таковыми, к примеру, являются следующие.
1. Продольные или крутильные колебания стержня постоянного поперечного сечения (рис. 2). В случае продольных колебаний u x, t – продольное отклонение в момент време-
ни t элемента стержня с координатой x от своего равновес-
ного положения, а |
a |
E |
, |
|
|
||||
|
|
|
стержня, – плотность.
где
E
– модуль Юнга материала
8
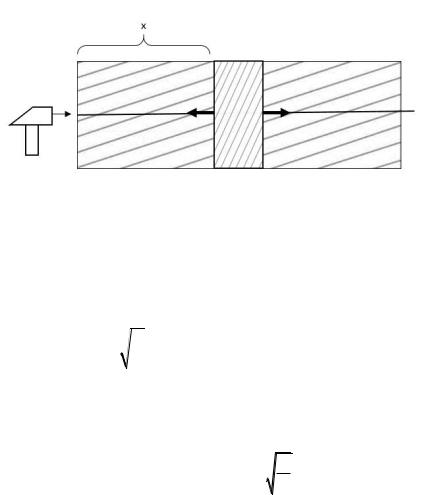
Рис. 2. Продольные колебания стержня постоянного сечения
В случае крутильных колебаний
u x, t
– угол поворота
поперечного сечения стержня с координатой
x
в момент
времени
t,
а a |
|
C |
|
. В этой формуле |
C – крутильная жѐст- |
|
I |
||||||
|
|
|
|
|
кость стержня, а I – момент инерции единицы длины стержня относительно его продольной оси. В случае стержня кругового сечения радиуса R их можно рассчитать по формулам
C G |
R4 |
I |
R4 |
|
|
; |
. |
||
|
||||
|
2 |
|
|
2 |
сдвига материала.
Поэтому
a |
G |
, |
|
|
|||
|
|
где G – модуль
2.Плоские акустические (звуковые) волны в жидкостях
игазах (рис. 3). В этом процессе волновому уравнению под-
чиняются возмущения давления |
p |
и плотности |
|
среды или |
потенциал скорости. Для изэнтропических (адиабатических)
9

течений сред с уравнением состояния
p f
скорость
a
распространения
выражением |
a |
2 |
|
возмущений
|
dp |
|
|
|
|
||||
d |
|
|||
|
|
0 |
||
|
|
|
|
f
(скорость звука) определяется
|
. |
В частности, если |
0 |
|
|
|
|
|
||
p p |
, |
|||||
|
|
|
|
|||
0 |
|
|
|
|||
|
|
0 |
|
|
||
|
|
|
||||
где
|
c |
p |
|
||
|
|
|
|
c |
|
|
V |
|
– показатель адиабаты газа, то
a |
p |
, |
где |
p0 |
и |
0 |
|
|
0 |
||||||
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
и плотности среды.
– невозмущѐнные значения давления
Рис. 3. Плоские акустические волны
3. Распространение электрических возмущений в линии
(рис. 4) при отсутствии потерь. При этом явлении |
u x, t |
|
есть напряжение или сила тока в момент времени t |
на эле- |
|
ментах проводов с координатой x. В случае, когда |
L |
и С |
есть распределѐнные соответственно индуктивность |
и |
ѐм- |
кость проводов в расчѐте на единицу длины,
a |
1 |
. |
|
LC |
|||
|
|
10
