Линейные свойства проекций

При сложении двух векторов и их проекции на произвольную ось складываются.

При умножении вектора на любое число проекция этого вектора на произвольную ось также умножается на число .

4.5. Декартова прямоугольная система координат

В реальном трехмерном пространстве положение каждой точки определяется тройкой действительных чисел.

Определение. Декартова прямоугольная система координат представляет собой три взаимно перпендикулярные оси в пространстве с общим началом О и одинаковой масштабной единицей:

о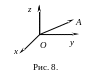 сь Оx – ось абсцисс;

ось Оy – ось ординат;

ось Оz – ось аппликат.

Направленныйотрезок называется радиус-вектором.

Декартовой прямоугольной системе координат отвечает тройка взаимно ортогональных единичных базисных векторов , , . Для произвольного вектора найдется единственная тройка чисел такая, что будет справедливо равенство:

, (4.4)

, , ,

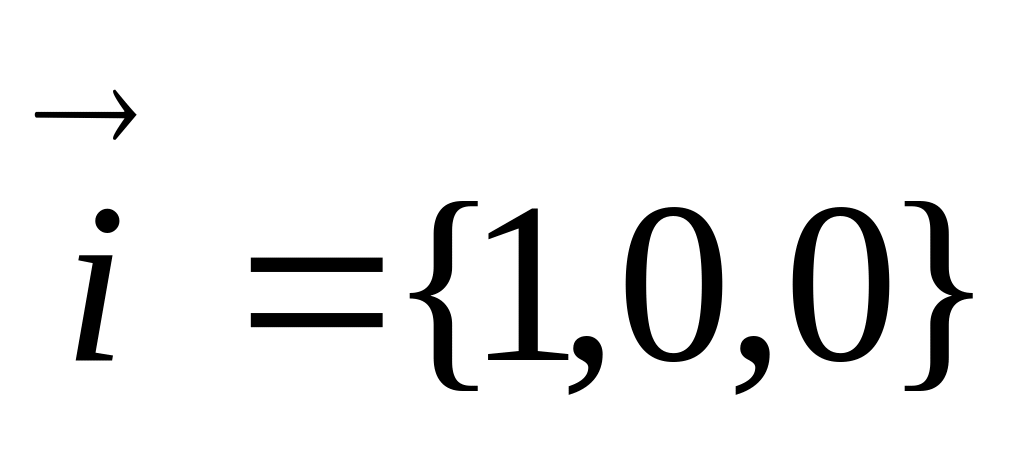– декартовы прямоугольные координаты , .

Т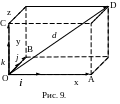 еорема 3. Декартовы прямоугольные координаты x, y, z вектора равны проекциям этого вектора на оси Оx , Оy , Оz соответственно.

;

, а так как - единичные векторы,то .

Обозначим , - углы наклона вектора к осям Ox, Oy, Oz.

Определение. Числа , , 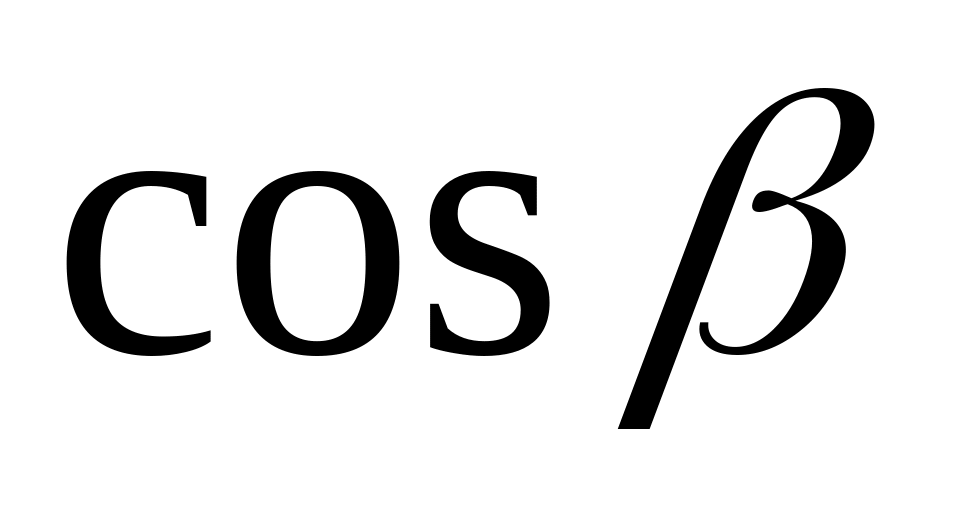принято называть направляющими косинусами вектора .

Из теоремы 2 и теоремы 3 вытекает, что

; ; _. (4.5)

Учитывая, что - диагональ прямоугольного параллелепипеда, имеем выражение длины вектора, а также направляющих косинусов через его координаты

(4.6)

(4.7)

Из равенств (4.7) следует, что сумма квадратов направляющих косинусов любого вектора равна 1

Вектор однозначно определяется заданием его длины и трех направляющих косинусов.

4.6. Формулы деления отрезка в данном отношении р ассмотрим в пространстве две точки и и прямую, определяемую этими точками.

Точки и определяют направленный отрезок .

Пусть любая отличная от и точка прямой.

Число называется отношением, в котором точка делит направленный отрезок .

Если спроецировать точки на координатную ось, то точка делит направленный отрезок в отношении , т.е. .

; , тогда , отсюда

; ; - (4.8)

- формула для нахождения координат точки, делящей отрезок в заданном соотношении

Если =1, то делит отрезок пополам.

Тогда

; ; . (4.9)

4.7. Произведение векторов: скалярное, векторное, смешанное

4.7.1. Скалярное произведение

Определение. Скалярным произведением двух векторов называется число, равное произведению длин этих векторов на косинус угла между ними. Обозначение или .

, (4.10)

где - угол между и .

Физический смысл – скалярное произведение- это работа вектора силы вдоль вектора .

Произведение - есть проекция вектора на ось, определяемую вектором , или же - проекция вектора на ось, определяемую вектором , гдеугол - угол между и .

Определение. Скалярным произведением двух векторов называется число, равное произведению длины одного из этих векторов на проекцию другого вектора на ось, определяемую первым из указанных векторов.

_, (4.11)

. (4.12)

Геометрические свойства скалярного произведения

Теорема. Необходимым и достаточным условием ортогональности двух векторов является равенство нулю их скалярного произведения.