2.3. Ранг матрицы

Пусть дана матрица, содержащая m строк и n столбцов

А = . (2.4)

Выделим в ней произвольным образом k строк и k столбцов. Элементы, которые находятся на пересечении выделенных строк и столбцов, образуют квадратную матрицу k-го порядка; определитель этой матрицы называется минором k-го порядка матрицы А. Очевидно, что в общем случае таких миноров k-го порядка может быть несколько. При этом максимальный порядок миноров равен минимальному из чисел m и n, т. е.

max k = min(m,n)

Из всех возможных миноров матрицы А выделим те из них, которые отличны от нуля. В свою очередь, среди этих миноров можно найти по крайней мере один минор наибольшего порядка.

Определение 1. Наибольший порядок миноров, отличных от нуля, называется рангом матрицы (2.4).

Вычисление ранга матрицы приведением ее к ступенчатому виду:

Идея: изменять матрицу А размера m´n так, чтобы сохранялся ее ранг. В результате матрица приводится к виду:

	; , (2.5)
m-r{

Матрица (2.5) имеет ступенчатый вид , где , * - некоторые числа.

Ранг этой матрицы = r.

Ранг матрицы не меняют следующие операции:

1. Прибавление к одной строке другой строки, умноженной на число.

2. Перемена местами строк, столбцов.

3. Умножение всех элементов какой-либо строки (столбца) на постоянное число .

Вычисление ранга матрицы:

1. Рассмотрим элемент . Пусть , тогда умножая первую строку на подходящие числа (для 2-ой ( ), для 3-ей ( )) и прибавляя ее ко 2-ой и 3-ей и т. д. строкам, преобразуем матрицу так, чтобы элементы первого столбца были равны нулю, тогда матрица примет вид:

.

Рассмотрим матрицу , образованную элементами 2-й, ..., n-й строк и столбцов. Добьемся того, чтобы , переставляя местами строки. Если этого сделать нельзя, то матрица уже имеет ступенчатый вид. Проделаем те же операции, что и с матрицей А, и так до тех пор, пока матрица не примет вид (2.4).

Пример 2.2. Найти ранг матрицы

А= .

Решение. Приведем матрицу к ступенчатому виду:

~ ~ .

1. Умножим каждый элемент 1-ой строки на (-2) и сложим со второй строкой; на (-4) и сложим с третьей строкой .

2. Умножим каждый элемент 2-ой строки на (-3) и сложим с 3-ей строкой.

3. Нетрудно увидеть, что максимальный порядок миноров этой матрицы отличных от нуля равен двум, поскольку минор третьего порядка содержит элементы 3-ей строки, которые равны нулю, следовательно определитель третьего порядка равен нулю, таким образом r(A) = 2.

2.4. Вычисление обратной матрицы

Пусть дана невырожденная матрица n-го порядка

А = , (2.6)

т. е. ее определитель не равен нулю. Рассмотрим матрицу , составленную из алгебраических дополнений к элементам матрицы А, с которой проведена операция транспонирования

= , (2.7)

Матрица называется присоединенной. Тогда обратная матрица равна

. (2.8)

Пример 2.3. Дана матрица . Вычислить обратную матрицу .

Решение. Вычислим определитель матрицы

Найдем алгебраические дополнения матрицы:

.

Вопросы для самопроверки

1. Что называется определителем? Каковы основные свойства определителя?

2. Что называется минором и алгебраическим дополнением? Приведите примеры.

3. Каковы способы вычисления определителей? Приведите примеры.

4. Что называется рангом матрицы? Как его можно найти?

5. Какая матрица называется обратной для данной матрицы? Как можно найти обратную матрицу?

Задачи для самостоятельного решения

Вычислить определители:

1. 

Ответ. -4.

2. 

Ответ. 180.

3. 

Ответ. 87.

4.

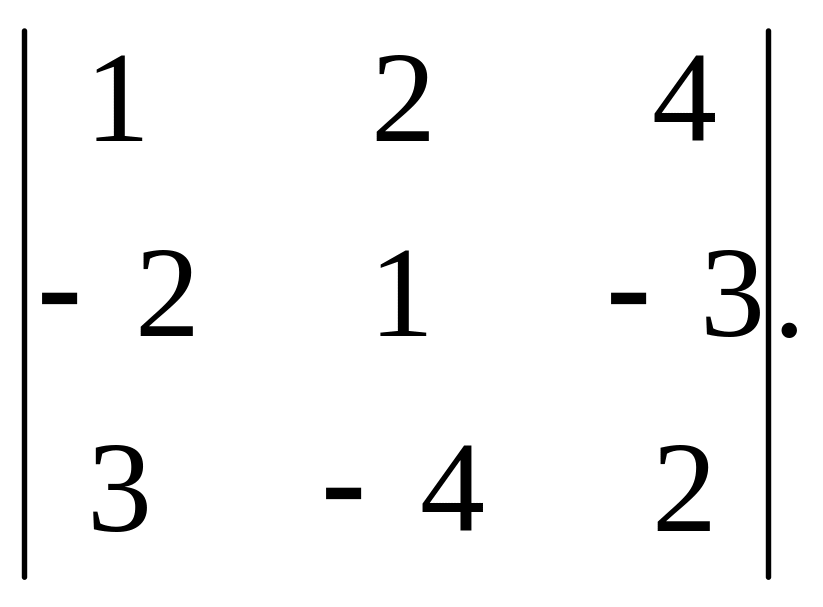
Ответ. 0.

5. Дана матрица Найти обратную матрицу.

Ответ.

6. Дана матрица Найти обратную матрицу.

Ответ.

3.СИСТЕМЫ ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ

УРАВНЕНИЙ