8.3. Каноническое уравнение параболы

Парабола представляет собой линию пересечения кругового конуса с плоскостью, параллельной одной из образующих конуса.

Определение. Параболой называется геометрическое место точек плоскости, для которых расстояние до некоторой фиксированной точки F этой плоскости равно расстоянию до некоторой фиксированной прямой, также расположенной в данной рассматриваемой плоскости.

Точка F – называется фокусом параболы, а фиксированная прямая - директрисой (направляющей) параболы.

Пусть . Тогда согласно определению

r = d – необходимое и достаточное условие расположения точки М(х, у) на данной параболе.

Пусть , тогда F( .

Тогда r = ,

d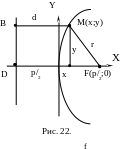 = Þ

= .

Упрощаем:

(х - .

Отсюда

-рх + у² = рх,

у² = 2рх

- каноническое уравнение параболы.

Из этого уравнения видно, что парабола симметрична относительно оси 0х.

Еe верхняя половина определяется уравнением

у = (0£ х < ).

Точка пересечения с осью симметрии называется вершиной параболы. Величина р – называется параметром параболы. Так как р > 0, то вся парабола расположена в правой полуплоскости 0ху. (Для р < 0 парабола расположена в левой полуплоскости).

Директриса параболы, определяемой каноническим уравнением у² = 2рх (р > 0) имеет уравнение

у = . (8.8)

Используя понятие фокуса и директрисы, можно определение параболы сформулировать так: парабола есть геометрическое место точек плоскости, для которых отношение расстояния до фокуса к расстоянию до директрисы есть величина постоянная, равная единице.

Аналогично, и для эллипса, отличного от окружности и для гиперболы: для каждого фокуса эллипса или гиперболы можно указать такую прямую, называемую директрисой, что отношение расстояния от точек этих кривых до фокуса к расстоянию до отвечающей этому фокусу директрисы есть величина постоянная.

8.4.Эксцентриситет эллипса и гиперболы

Пусть с – половина расстояния между фокусами эллипса (гиперболы), а – большая полуось эллипса (действительная полуось гиперболы).

Определение. Эксцентриситетом эллипса (гиперболы) называется величина

(8.9)

Учитывая, что для эллипса , Þ ,

для гиперболы , , имеем

(8.10)

для эллипса;

(8.11)

для гиперболы .

Таким образом, эксцентриситет эллипса меньше 1, а гиперболы больше 1. Эксцентриситет окружности равен 0 (т.к. = а).

При одинаковых эксцентриситетах два эллипса или две гиперболы подобны.

Эксцентриситет эллипса можно рассматривать как меру его «вытянутости».

Эксцентриситет гиперболы можно рассматривать как числовую характеристику величины раствора угла между её

а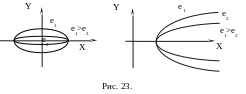 симптотами.

8.5. Директрисы эллипса, гиперболы

8.5.1. Директрисы эллипса

Пусть дан эллипс: F₁ и F₂ фокусы, - эксцентриситет. Малая ось эллипса делит плоскость на две p₁ и p_{2 ,} а – большая полуось.

Определение: Директрисой (i = 1,2) эллипса, отвечающей фокусу F_i (i =1,2), называется прямая, расположенная в полуплоскости p_i (i =1, 2), перпендикулярной большой оси эллипса, на расстоянии от его центра.

З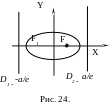 амечание 1. Уравнение директрисы можно записать в виде

D₁ : х = (8.12)

D₂ : х =

Замечание 2. Директрисы эллипса расположены вне эллипса, поскольку эллипс находится в прямоугольнике.êх ê£ а; , а директрисы на расстоянии

> а (0< < 1).

Замечание 3. Точки эллипса и его центр расположены по одну сторону от каждой его директрис.

Замечание 4. Обозначим через р – расстояние от фокуса до соответствующей ему директрисы.

Так как расстояние от центра до директрисы равно , а от центра до фокуса с, то р = , а так как с = а , то

р = а (8.13)

- расстояние от фокуса до соответствующей ему директрисы.

Теорема. Отношение расстояния r_i от точки М эллипса до фокуса F_i к расстоянию d_i от этой точки до отвечающей этому фокусу директрисы равно эксцентриситету этого эллипса.