Вопросы для самопроверки
Что называется матрицей? Как определяются линейные операции над матрицами и каковы их свойства?
Что называется произведением двух матриц? Каковы свойства произведения матриц?
Какая матрица называется единичной?
Задачи для самостоятельного решения
1. Найти сумму матриц
,
.
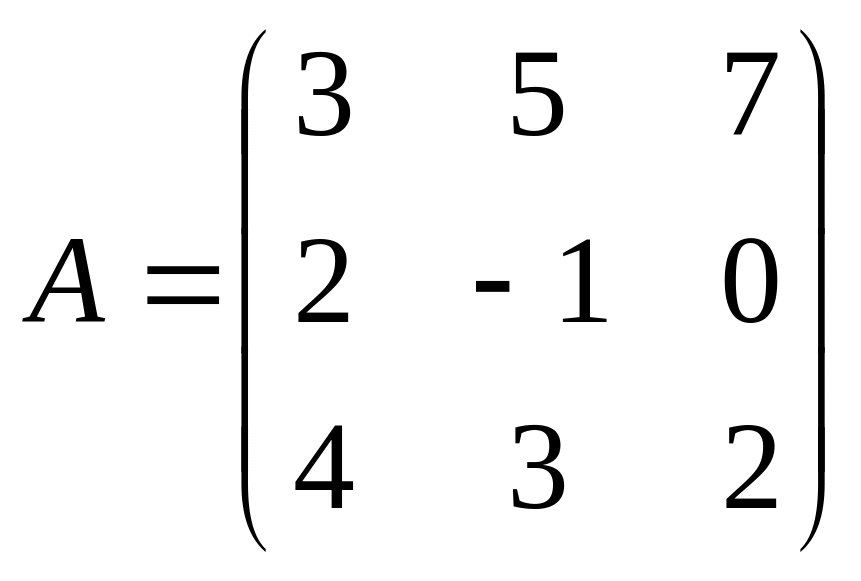Ответ.
.
2. Найти матрицу 2А+5В, если
,
.
Ответ.
.
3.
Найти значение матричного многочлена
2А2+3А+5Е
при
, если Е
–единичная матрица третьего порядка.
Ответ.
.
4.
Найти матрицу АВ,
если
,
В=
.
Ответ.
АВ=
.
5. Дана матрица
.
Найти матрицу
.
Ответ.
6. Даны матрицы А и В :
.
Найти
Ответ.
,
Определители
Операции над определителями
Любой квадратной матрице А порядка n ставится в соответствие по определенному закону некоторое число, называемое определителем или детерминантом n-го порядка этой матрицы. Начнем с определителей второго и третьего порядков.
Пусть дана матрица
А=
,
Тогда ее определитель второго порядка вычисляется по формуле
det
A=
=
(2.1)
Правило вычисления определителя второго порядка очевидно: из произведения элементов на главной диагонали вычитается произведение элементов на второй диагонали матрицы А.
В дальнейшем мы не будем приводить матрицу, для которой вычисляется определитель, так как в записи определителя содержится все элементы соответствующей матрицы.
Определитель третьего порядка вычисляется по формуле
(2.2)
Правило вычисления определителя третьего порядка таково. Это алгебраическая сумма шести тройных произведений элементов, стоящих в разных строках и разных столбцах; со знаком “плюс” берутся произведения, сомножители которых находятся на главной диагонали и в вершинах треугольников с основаниями, параллельными главной диагонали; со знаком “минус” – произведения, сомножители которых стоят не на главной диагонали и в вершинах треугольников с основаниями, параллельными этой диагонали (рис. 1).
Порядок определителя равен порядку соответсвующей матрицы.
2.2. Основные свойства определителя
1. Величина определителя не изменяется, если строки и столбцы этого определителя поменять местами, т. е.
=
.
2. Перестановка двух строк (или двух столбцов) определителя равносильна умножению его на число (-1).
3. Если определитель имеет две одинаковые строки (или столбца), то он равен нулю.
4. Умножение всех элементов некоторой строки (столбца) определителя на число равносильно умножению определителя на это число , т. е. общий множитель всех элементов некоторой строки (столбца) определителя можно выносить за знак определителя:
=
.
5. Если все элементы некоторой строки (столбца) определителя равны нулю, то и сам определитель равен нулю.
6. Если элементы двух строк (столбцов) определителя пропорциональны, то определитель равен нулю.
7. Если каждый элемент n-ой строки (столбца) представляет собой сумму двух слагаемых, то определитель может быть представлен в виде суммы определителей, первый из которых имеет в n-ой строке (столбце) первые из упомянутых слагаемых и те же элементы, что и исходный определитель в остальных строках (столбцах), а второй определитель имеет в n-ой строке (столбце) вторые из упомянутых слагаемых и те же элементы, что и исходный определитель, в остальных строках (столбцах):
=
+
.
8. Если к элементам некоторой строки (столбца) определителя прибавить соответствующие элементы другой строки (столбца), умноженные на произвольный множитель , то величина определителя не изменится.
=
+
,
=0.
Минором
элемента
определителя
n-го
порядка называется определитель (n-1)-го
порядка, получаемый из данного определителя
путем вычеркивания тех строки и столбца,
на пересечении которых стоит данный
элемент. Это число
.
Алгебраическим дополнением любого элемента определителя называется число, равное минору этого элемента, взятому со знаком (+), если сумма номеров строки и столбца элемента, есть число четное и со знаком (-) – в противном случае
, (2.3)
например,
;
;
.
9. Разложение определителя по строке (столбцу). (Один из способов вычисления определителя) Сумма произведений элементов какой-либо строки (столбца) на соответствующие алгебраические дополнения элементов этой строки (столбца) равна величине этого определителя.
Определитель 3-го порядка разложим по первой строке
=
-
+
;
Пример 2.1. Вычислить определитель четвертого порядка
.
Разложить определитель можно по любой строке (столбцу). Однако объем вычислений можно существенно уменьшить, если выбрать такую строку (столбец), в которой больше элементов, равных нулю. Наиболее подходящей в нашем случае является вторая строка. Разложение по ней определителя имеет вид
=
=3(3 +14 + 48 – 126 – 2 - 8) + 2(4 + 24 + 36 - 48 - 9 - 4)= -207.
10. Сумма произведений элементов некоторой строки (столбца) определителя на соответствующее алгебраическое дополнение другой строки (столбца) равна нулю.
11.
Произведение двух определителей n-го
порядка с элементами
есть в свою очередь определитель n-го
порядка с элементами
:
.
12. При транспонировании матрицы определитель не меняется.