3.1. Общий вид и свойства системы уравнений
Система m
линейных уравнений с n
неизвестными (переменными)
имеет
вид
(3.1)
Здесь
и
-произвольные
числа (i=1,
2, ..., m;
j=1,
2, ..., n),
которые называются соответственно
коэффициентами
при
неизвестных и свободными членами
уравнений
(3.1). Первый индекс у коэффициентов при
неизвестных означает номер уравнения,
и второй индекс соответствует номеру
неизвестного
.
Решением
системы уравнений
(3.1) называется набор n
чисел
,
при подстановке которых в эту систему
каждое уравнение данной системы
превращается в тождество.
Система уравнений(3.1) называется совместной, если она имеет хотя бы одно решение; если система не имеет решений, она называется несовместной. Совместная система уравнений имеет либо одно решение, и в таком случае она называется определенной, либо, если у нее больше одного решения, она называется неопределенной.
Системы уравнений вида (3.1) называются эквивалентными, если они имеют одно и то же множество решений. Элементарные преобразования исходной системы приводят к эквивалентной системе. К элементарным преобразованиям относятся:
вычеркивание уравнения
-нулевой
строки;
перестановка уравнений или слагаемых
в уравнениях
прибавление к обеим частям одного уравнения соответственно обеих частей другого уравнения этой системы, умноженного на любое действительное число.
3.2. Матричная форма системы уравнений
Сведем коэффициенты при неизвестных в системе уравнений (3.1) в матрицу
А = . (3.2)
Эта матрица состоит из m строк и n столбцов и называется матрицей системы. Введем в рассмотрение две матрицы-столбца: матрицу неизвестных Х и матрицу свободных членов В:
A=
,
B=
. (3.3)
Тогда
систему линейных уравнений (3.1) можно
записать в матричной форме, поскольку
размер матрицы А
равен m
n,
а размер Х-
n
1,
значит, произведение этих матриц имеет
смысл:
АХ=В. (3.4)
Введем
в рассмотрение еще одну матрицу; дополним
матрицу системы А
столбцом свободных членов и получим
новую матрицу размера
:
.
Матрица
называется
расширенной
матрицей системы.
Теорема 3.2. (теорема Кронекера-Капелли; критерий совместности системы). Система линейных алгебраических уравнений совместна тогда и только тогда, когда ранг матрицы системы равен рангу расширенной матрицы системы.
3.3. Метод обратной матрицы и теорема Крамера
Рассмотрим частный случай системы (3.1) , когда число уравнений равно числу неизвестных, т. е. m=n. Система уравнений имеет вид
.
(3.5)
Составим квадратную матрицу А 3-го порядка этой системы:
.
(3.6)
В матричной форме система уравнений (3.5) имеет вид (3.4):
АХ=В,
где матрицы Х
и В имеют
размер
.
Пусть матрица системы А
является невырожденной, т. е существует
обратная матрица А-1.
Умножив обе части этого уравнения слева
на
получаем решение системы (3.5) в матричной
форме:
(3.7)
Вычисление обратной матрицы по заданной матрице А производится по формулам (2.3) и (2.8).
В случае когда порядок n
матрицы А
и
достаточно велик, вычисление обратной
матрицы может быть очень сложным.
Другой метод решения системы уравнений (3.6) основан на теореме Крамера. Составим определитель матрицы системы А:
,
(3.8)
который называется также определителем системы.
Теорема
3.3. (теорема
Крамера).
Пусть
- определитель матрицы А
системы, а
-определители, полученные из определителя
заменой j-го
столбца столбцом свободных членов В,
называемые
дополнительными определителями.
Тогда, если
, система линейных уравнений (3.6) имеет
единственное решение, определяемое по
формулам
(3.9)
Формулы вычисления неизвестных (3.9) – решения системы (3.6) –носят название формул Крамера.
Пример 3.1. Найти решение системы уравнений
Решение. Применим метод обратной матрицы
.
Определитель системы:
=
=
=1(2 - 20) - 2(8 - 12) + 3(20 - 3) = -18 + 8 + 51 = 41.
Алгебраические дополнения:
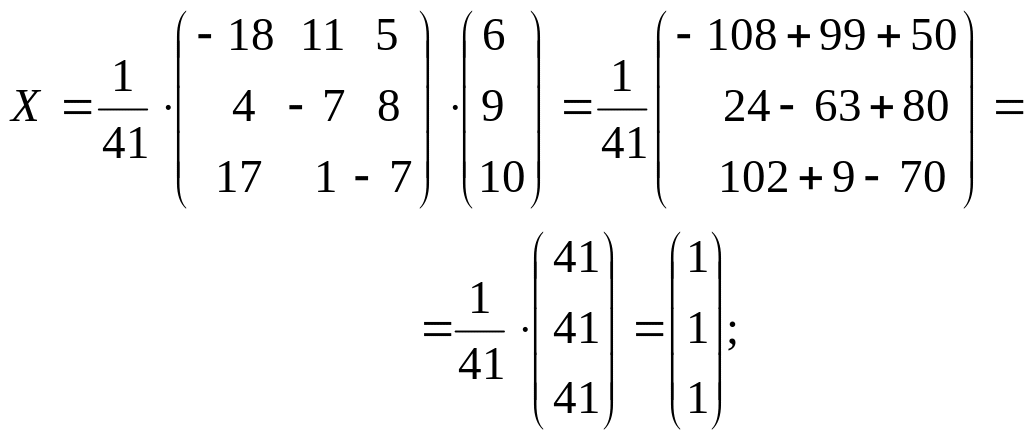
x=1; y=1; z=1.
Решим
систему, применяя формулы Крамера.
Определитель системы:
отличен от нуля, следовательно система
имеет единственное решение.
Вычисляем
определители:
;
;
:
Тогда:
,
,
.