6.3. Параметрическое уравнение прямой
Примем за параметр
величину
=
t, тогда область
определения t: -¥
< t
< ¥.
Мы получим х – х1 = lt,
у – у1 = mt.
Таким образом
х
=
(6.6)
у =
- параметрические уравнения прямой.
6.4. Уравнение прямой с угловым коэффициентом
у
Т
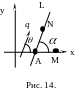ангенс
угла наклона прямой к оси
назовем угловым коэффициентом
этой прямой:
.
Для прямой, параллельной оси
k = 0, для прямой, перпендикулярной оси , k не существует. Если прямая не параллельна оси и имеет направляющий вектор = , то угловой коэффициент этой прямой k:
(6.7)
(т. е.
=
;
,
а
или
).
Умножив обе части
канонического уравнения
на m, получим:
у – у1 = k(х – х1) (6.8)
- уравнение прямой, проходящей через точку М1(х1, у1) и имеющей заданный угловой коэффициент k.
Если обозначить постоянную у1 – kx1 = b, то (6.8) примет вид
у = kx + b (6.9)
- уравнение прямой с угловым коэффициентом.
6.5. Угол между двумя прямыми. Условие параллельности и перпендикулярности двух прямых
6.5.1. Прямые заданы общими уравнениями
Пусть две прямые
и
заданы общими уравнениями А1х
+ В1у + С1 = 0
и А2х + В2у
+ С2 = 0 .
Задача об определении угла между прямыми сводится к определению угла между нормальными векторами
=
и
=
.
Из определения
скалярного произведения (
)
имеем
(6.10)
- угол между прямыми.
Условие параллельности эквивалентно условию коллинеарности векторов и :
. (6.11)
Так как cosj
= 0, при
,
то условие перпендикулярности:
.
(6.12)
6.5.2. Прямые заданы каноническими уравнениями
Пусть L1 и L2 заданы каноническими уравнениями:
,
,
где
направляющие векторы
= {l1, m1}
и
= {l2, m2},
тогда
cos
=
,
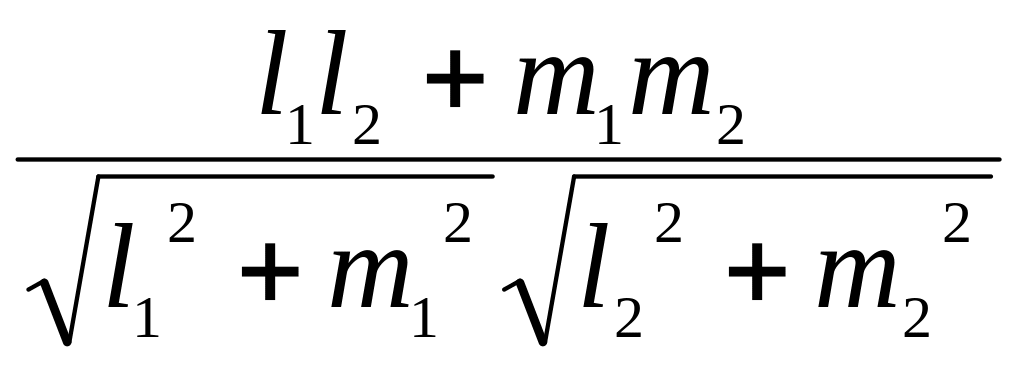(6.13)
=
, (6.14)
+
= 0 (6.15)
- угол между прямыми, условие параллельности, перпендикулярности прямых, соответственно.
6.5.3. Прямые заданы уравнениями с угловым коэффициентом
П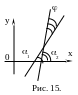
усть
и
заданы уравнениями с угловым
коэффициентом у = k1х+
b1 и у = k2x
+ b2;
и
-
углы наклона прямых. Тогда
=
-
- угол между прямыми.
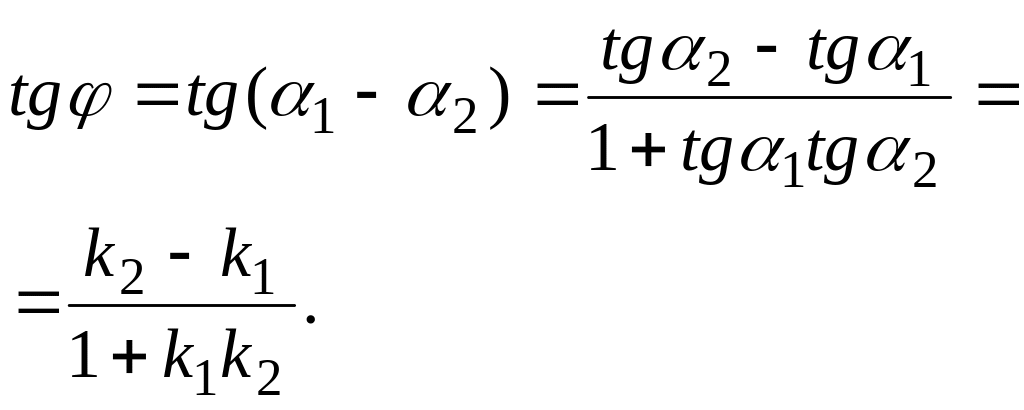
(6.16)
- угол между прямыми.
Прямые параллельны,
если
= 0, т.е.
(6.17)
– условие параллельности.
Условие перпендикулярности
– это условие того, что tgj
не существует, т.е. 1 +
= 0, отсюда
(6.18)
- условие перпендикулярности.
Вопросы для самопроверки
Как записывается общее уравнение прямой на плоскости?
Как записываются параметрические уравнения прямой на плоскости?
Что называется угловым коэффициентом прямой на плоскости и каков его геометрический смысл в декартовой прямоугольной системе координат?
Как записывается уравнение прямой, проходящей через две точки на плоскости?
Как вычисляются углы между двумя прямыми на плоскости? Каковы условия параллельности и перпендикулярности двух прямых на плоскости?
Задачи для самостоятельного решения
1. Даны вершины
треугольника АВ С :
Определить внутренний угол при вершине
А.
Ответ.
.
2. Даны стороны
треугольника:
,
.
Составить уравнения его высот.
Ответ.
.
3. Даны вершины
треугольника
Составить уравнения медианы, проведенной
из вершины В ,и высоты, опущенной из
вершины С . Вычислить площадь
треугольника.
Ответ.
,
,
кв.ед.
7. ПРЯМАЯ В ПРОСТРАНСТВЕ
7.1. Общее и канонические уравнения прямой
в пространстве
Прямую линию, являющуюся пересечением двух различных плоскостей, определяемых уравнениями
и
,
можно задавать двумя уравнениями этих
плоскостей, т. е.
-
(7.1)
- общее уравнение прямой в пространстве.
Однако более удобным для решения задач является канонический вид уравнений прямой.
Пусть прямая
проходит через данную точку
(х1,
у1,z1)
и имеет заданный направляющий вектор
.
Точка
(х,
у, z) лежит на этой
прямой тогда и только тогда, когда
векторы
=
и
коллинеарны, т.е. их координаты
пропорциональны
(7.2)
- канонические уравнения прямой в пространстве, где хотя бы одно из чисел l,m, n ¹ 0.
Прямую,
заданную общими уравнениями можно
привести к каноническому виду. Для этого
необходимо найти координаты точки ,
лежащей на прямой, и координаты
направляющего вектора этой прямой.
Общее уравнение прямой (7.1) представляет
систему двух уравнений с тремя
неизвестными, решением которой является
множество точек (множество решений),
лежащих на прямой, из которых нам
необходимо выбрать одну. Для этого
положим
и найдем координаты
и
,
решая систему уравнений
.
Для нахождения
координат l, m,
n вектора
,
заметим, что
ортогонален каждому из нормальных
векторов плоскостей
=
и
=
.
Так что можно положить
=
.
Тогда
;
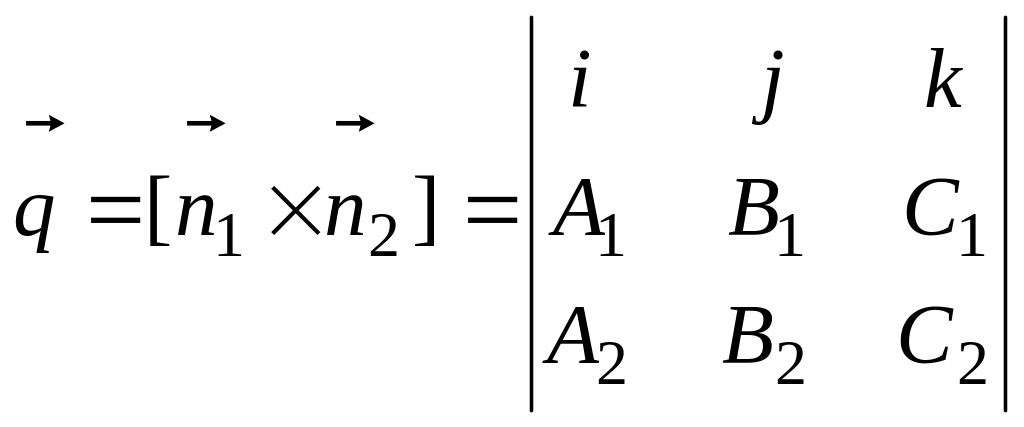l = b1c2 – b2c1; m = C1A2 – C2A1; n = A1B2 – A2B1.
Пример 7.1. Привести общее уравнение прямой
к каноническому виду.
Решение. Найдем
координаты точки, через которую проходит
прямая. Положим
,
тогда
,
отсюда
.
Найдем координаты направляющего вектора прямой.
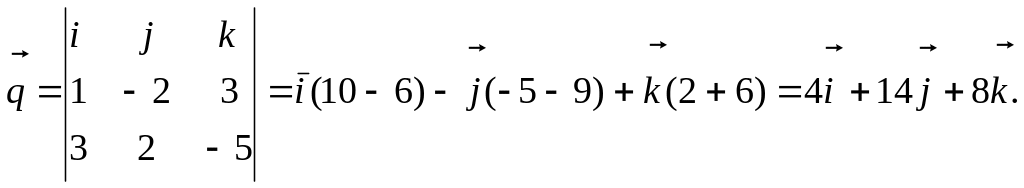
Тогда канонические уравнения прямой имеют вид
или 
.
7.2. Уравнение прямой, проходящей через две
заданные точки
Уравнение прямой, проходящей через две различные точки М1(х1, y1, z1) и М2(х2, y2, z2) имеет вид
,
(7.3)
где
направляющий вектор
=
.
Пример 7.2. Составить канонические уравнения прямой, проходящей через две заданные точки (1,-2,1) и (3,1,-1)
Решение. Применяя формулу (7.3), имеем
.
Тогда канонические уравнения прямой
имеют вид
.
7.3. Параметрические уравнения прямой
в пространстве
Параметрические уравнения прямой в пространстве получаются из канонических уравнений (7.2).
Приравняем параметру каждое из соотношений (7.2),
,
следовательно x– х1 =lt; y – y1= mt; z - z1= nt,
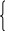x =x1
+lt,
y = y1 +mt, (7.4)
z = z1 + nt
- параметрические уравнения прямой.
Пример 7.3. Составить
параметрические уравнения прямой
Решение. Найдем координаты точки, лежащей на прямой. Положим .Тогда система уравнений примет вид
Решая эту систему,
получим
.
Следовательно на
прямой фиксирована точка
.
Найдем координаты направляющего вектора прямой
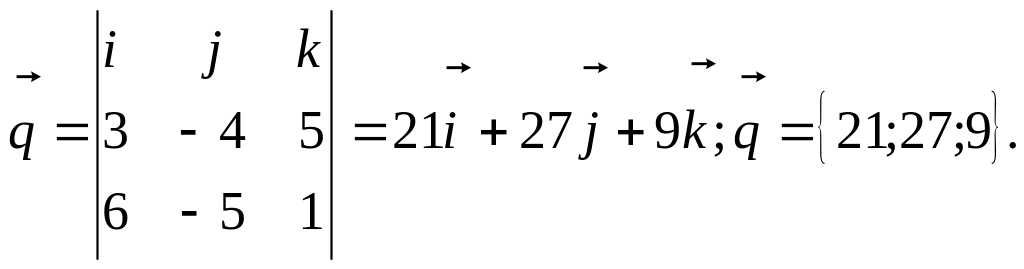
Тогда параметрические уравнения прямой примут вид
