ТФКП Краснов 2003

§ 13. Конформные отображения

137

iflайти образы следующих областей при заданных дробио-линейный отображе­

.

zz +1

471 . Кольцо l < lzl < 2 nри w = --2 .

.

.

+

z + i

472.

при w =

Внешность круга lzl >

. .

473.

Круг

· 1 лри w

z1- 1

z -

lzl <

-· -

= --. .

474. Оnределить, во что

z + •

lzl

< 1

переходит внутренность круга

при дробно­

которое·

переводит точки

z1

=

i,

z3 = оо

·,пинейном: отображении,

w2

оо, w3 = 1 .

1,

z2

=·

tоответственно-в точки w1 = О,

1 +

i

;475.

Найти точки, симметричные с точкой z

=

относительно следующих

if:fиний:

lzl =

v'2;

lz -

il = 2.

·а) ж =

О;

б)

в)

линейной функции, отображающей:

Найти общий вид дробио-

1 -

а476.) верхнюю полуплоскость на нижнюю полуnлоскость;

· )

верхнюю полуплоскость на правую nолуnлоскость

w(O) = 1,

w(l)

2,

w(2) = оо.

_1478.

Найти отображение на единичный круг · 1w1

< 1 верхней nолуплоскости

)m z

>

.О так, чтобы

-

;

:!!).

2

w(2i) = О, arg w'(2i) = О.

l

w(i) = О, argw'(i) =

б)

479.

Найти функцию w

f(z), отображающую верхнюю полуплоскость на еди­

круг так, .чтобы точки

z1

= -1, z2

= О,

z3

=.

1

переходили в точки

:;иичный w2

=

i,

=

(,.80.

l,

окружности.

lzl

<

1

Найти.

функциюWз -1w

=

/(z),

отображающую-

круг

на

нижнюю

L:W1

1 ' о. - 1 .

r··иолуплоскость так,

чтобы точки 1 , i, -i

перешли в точки

-

i481 .

Найти дробио-линейную функцию, отображающую круг 'lzl

< 1 на nо­

Jiуnлоскость Im z > О

так,

чтобы точки

...l,:1 , i перешли в точки оо;

О, 1 .

75, 4 + Зi,

5 перешли в точки - 1, i, 1 .

lzl <

5 в круг

lwl

<

1

так, чтобы

r 82.

Найти конформное отображение круга

-483.

Найти функцию w = f(z),

отображаюшую конформно единичный круг

[ i .

(

1 )

.

'(1)

1r

1

а себя и такую, что

2

ra)

f

2 . = 0, arg f

= 2 ;

б)

/(0) = 0,

arg f (0) = - 2 ;

[484 .

Найти дробио-линейную функцию, отобр

ажаю

щую круг lz - 11 < 3 на круг

;1wl < 1

так, чтобы точки -1, 5, iyS i1epellU(И сооtветственио в точки 1 , i, - 1 .

138

Глава 4. Конформные отображения

z

1

485. На какую область в плоскости w отобразит функция w == i-- верхний

. полукруг izi < 1 ,

Imi > О?

D: l

:s.:;;

:s.:;;2,

О :s.:;;arg

z

:s.:;;

7Г

1

+z

486. Найти образ области

при отображении

1 .

izi

4

w = =z-+ 1 .

4° .

Конформные отображения, осуществляемые основ­

ными элементарными функциями.

. 1. Степенная функция

( 1 1)

где n 2 - целое положительное число.

Отображение, осуществляемое степенной функцией, является кон­

формным во всей nлоскости, кроме точки z =

0.:

при z

# О ·имеем

w' = nzn-l ; при·

z = О

w'

= О. Дри z = = Оконформность нарушается, так

как при отображении с помощью функции

(

1 1) углы увеличиваются.

в n

раз. Угол О

2

<

rp

- функцией ( 1 1) отображается взаимно однозначно

.

< n

на всю плоскость z с разрезом по Положительной части действительной

2

оси, причем лучу rp = О соответствует верхний, а лучу rp = - ..:..нижний

.

край разреза. Такое же отображение получим для каждого изnуглов, на ко- ·

2k

торые плоскость z разбивают лучи rp = -- (k. - цело число), причем

.

2(k - 1)

.

n

2k

при отображении угла

n

< rp < --n

(k == 1 , 2, . . . , n) на плоскость

2(k - 1)

.

верхний,

а

2k

с разрезом лучу rp =

n

соответствует

лУЧУ rp < - -

нижний край разреза.

n

Пример 1 5.

на единичный круг

Отобразить сектор О < arg z < '4

lwl < 1 так,

чтобы точка z1 = ei1r/S перешла в центр w1 = О, а точка

z2 О

-

в точку w2 = 1 .

z

7Г

а)

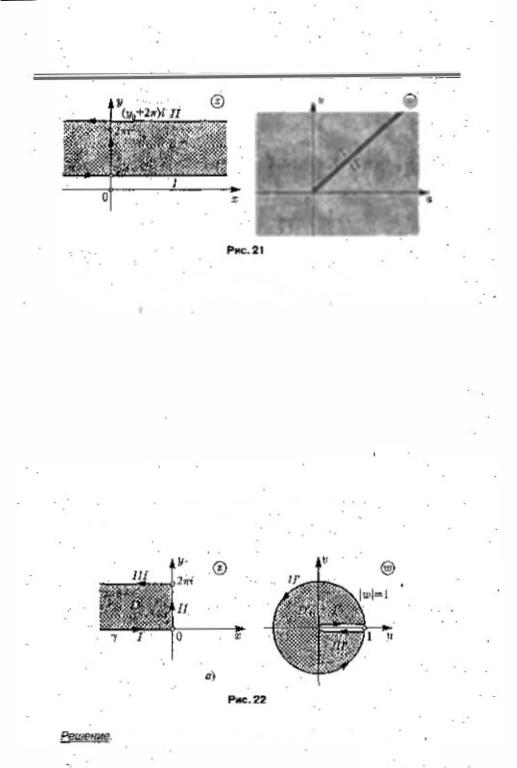
Решение.

Сектор О < arg

<

(рис. 19,

с помощью функции t ==

z4

'4

>

(рис. 19, б).

Точка z1 ==

отобразим на верхнюю полуплоскость

Imt

О

ei"/8

nерейдеТ В

ТОЧку t1 = zi

= i ,

а Z2

= 0 перейдет В ТОЧку t2 = 0.

'

Затем отобразим полуплоскость Im t >

О на круг lwl <

1

так,

чтобы точка

t1 =· i 'Перешла

в

центр круга

(рис. 19, в).

Воспользовавшись форм лой (9),

получим

.

i t - i

w

= e ' -' - .

t + i

140

Глава 4. Конформные отображения

части действительной оси на секторы

,

2(k - 1)1г

2k1Г

(k

= 1 , 2, . . . , n).

-'---'--<, arg w < -

n

n

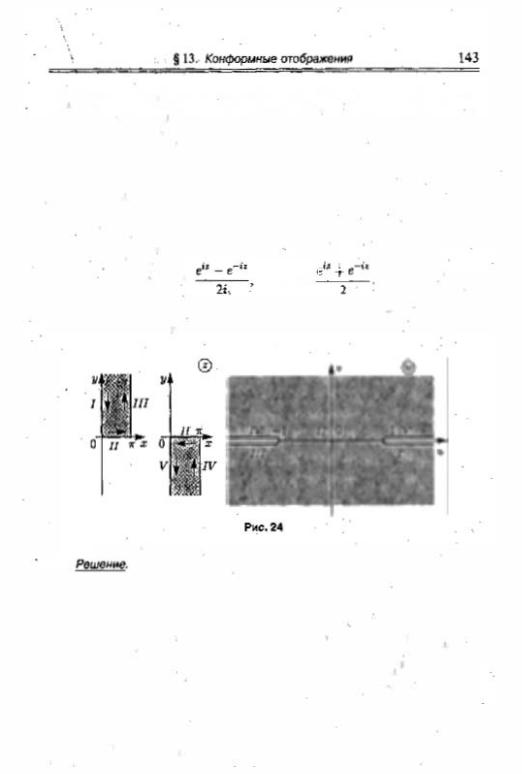
Пример 1 7. Отобразить верхнюю полуплоскость Im z > О с разрезом

по отрезку от точки z1

= О до точки

z2

= ai (а > О)

на верхнюю

полуплоскость Imw

> О

(устранить разрез).

Решение.· 1) С помощью отображения t = z2

удвоим углы в начале коор­

динат. При этом отрезок z 1 z2 перейдет в отрезок t 1 t2

расщиренной t-плоскости

от точки t 1 = О дq точки t2

=

2 , а луч arg z =

(отрицательная действительная

полуось) - в луЧ arg w = 21r-.аТаким образом,1r

исходная обласtь отобразилась

на расширенную t -nлоскость с разрезом от точки t2 =

-а2 до точки t = +оо.

2)· С помощью линейной

функции1

т

t + а2

сдвинем начало разреза

в начало координат. Расширенная т-плоскq

=

т = О до точки т = +оо.

3) С помощью фу кции

= . . / (Тточнее, ее ветви, nринимающей nоложи­

береrу разреза) отображаем разрезанную т -nлос-

тельные значения на верхнем w

·

кость на полуnлоскость Imw' > О . Итак,

.w

= vГr = = ..j

+

а2 .

[>

z2