
Белозеров В.И. Сборник задач по курсу «Техническая термодинамика»
.pdf7.19.Известно, что 1 кг пара расширяется адиабатно от начальных параметров P1 = 32 бар и t1 = 315 °C до P2 = 48 кПа. Определить h1, u1, h2, v2, X2 и работу расширения.
7.20.Известно, что 2,2 м3 влажного пара со степенью сухости X = 0,82 расширяются адиабатно от 5 до 0,5 бар. Определить степень сухости, объем пара в конце расширения и произведенную им работу.
7.21.Известно, что 1 кг пара расширяется адиабатно от началь-
ных параметров P1 = 95 бар и t1 = 470 °C до P2 = 0,035 бар. Найти значения h1, u1, h2, v2, X2 и работу расширения.
7.22.Влажный пар при P1 = 9,2 бар и X1 = 0,98 изоэнтропно расширяется до P2 = 0,46 бар. Определить степень сухости в конце расширения аналитическим и графическим методами.
7.23.Пар при давлении P1 = 2,1 МПа и температуре t1 = 380 °C расширяется адиабатно до конечного давления P2 = 0,09 бар. Определить степень сухости в конце процесса и давление, при котором пар в процессе расширения окажется сухим насыщенным.
7.24.Пар с начальным давлением 70 бар и температурой 390 °C
расширяется адиабатно до P2 = 0,04 бар. Определить начальные и конечные параметры и работу расширения 1 кг пара.
7.25.Определить количество тепла, затрачиваемого на перегрев 1 кг влажного пара при давлении P = 97 бар и степени сухости
X = 0,96 до температуры t = 450 °C.
7.26. Паровые котлы высокого давления имеют паропроизводительность 640 т/ч при давлении пара P = 14 МПа и температуре t = 570 °C. Температура питательной воды tв = 230 °C. Теплота сгорания топлива составляет 6000 ккал/кг. Чему равен часовой расход топлива, если КПД парового котла составляет 88,2 %?
7.27.Одна из паровых машин, созданных русским изобретателем И.И. Ползуновым, имела следующие размеры: диаметр цилиндра 0,81 м и ход поршня 2,56 м. Давление пара, поступающего в машину, составляло 1,2 ат. Считая пар, поступающий в машину, влажным насыщенным со степенью сухости Х = 0,975, определить массу пара в цилиндре машины.
7.28.В парогенераторе при давлении P = 15 бар и температуре
t = 280 °C протекает пар. Расход пара равен 380 кг/ч, скорость пара
61
w = 53 м/c. Определить диаметр паропровода, по которому протекает пар.
7.29.Паровая турбина расходует 54000 кг/ч пара. Отработавший
втурбине пар поступает в конденсатор при давлении Pк = 4,6 кПа и влажности 12 %. Определить часовой расход охлаждающей воды,
если ее начальная температура t1 = 15 °C, конечная t2 = 25 °C, а температура конденсата на выходе из конденсатора на 2 °C ниже температуры насыщения.
7.30. В барабане-сепараторе находится вода и над ней водяной пар под давлением P = 6,5 МПа. Масса воды m = 4600 кг. Объем барабана V = 8,3 м3. Считая пар сухим насыщенным, определить массу пара, находящегося над зеркалом испарения.
7.31. Известно, что 100 кг влажного пара с параметрами t1 = = 234 °C, X1 = 0,7 находится в сосуде. В сосуде отсепарировано и удалено 25 кг воды, причем давление все время поддерживалось постоянным. Определить параметры (P, v, h, s) оставшегося в сосуде пара.
7.32. При постоянном давлении смешиваются две порции водяного пара. Масса пара первой порции m1 = 250 кг, его параметры P1 = 1,3 МПа, X1 = 0,88. Масса пара второй порции m2 = 85 кг, его параметры P1 = P2 и X2 = 0,12. Определить степень сухости пара в образовавшейся смеси и его полную энтальпию.
Указание. Использовать свойство аддитивности энтальпии.
7.33. Влажный пар из турбины поступает в конденсатор со степенью сухости 0,88 при давлении P2 = 0,004 МПа. Определить расход охлаждающей воды на 1 кг поступающего пара, если вода нагревается на 12 °C, а температура конденсата на 3 °C меньше температуры насыщения.
7.34. При помощи s-h-диаграммы определить теплоту парообразования r при давлении P = 1,8 МПа. Сравнить результат с табличным значением. Для этого состояния выразить энтальпию влажного пара hX через r и h″. Значения hX и h″ определить по s-h-диаграмме.
Указание. На изобаре 1,8 МПа выбрать точку, отвечающую некоторой произвольной степени сухости X.
7.35. В начале растопки парового котла состояние пароводяной смеси определяется давлением P1 = 1 МПа и X1 = 0,01. За какое
62
время при закрытых вентилях на линии питательной воды и паровой магистрали давление пара в котле возрастет до P2 = 4,8 МПа, если мощность Q теплового потока, направленного от топочных газов к рабочему телу, равна 350 кВт, а масса пароводяной смеси m = 8 т? Потери теплоты при теплопередаче от газов к воде и водяному пару не учитывать.
7.36. В пароперегреватель котельного агрегата поступает водяной пар в количестве 15 т/ч. Определить сообщаемое пару часовое количество теплоты Q, необходимое для перегрева пара до t = 600 °C, если степень сухости пара перед входом в пароперегреватель X1 = 0,96, а абсолютное давление пара в пароперегревателе
P= 14,2 МПа. Изобразить процесс в s-T- и s-h-диаграммах.
7.37.Теплоэлектроцентраль отдает на производственные нужды заводу G = 20 т/ч пара при P = 0,7 МПа и X = 0,95. Завод возвраща-
ет конденсат в количестве 60 % G при температуре tв = 70 °C. Потери конденсата покрываются химически очищенной водой, имеющей температуру tхим = 90 °C. Сколько килограммов топлива в час нужно было бы сжечь в топке парового котла, работающего с КПД 80 %, если бы этот паровой котел специально вырабатывал пар, нужный заводу, и если теплота сгорания топлива Q = 30 МДж/кг?
7.38. В целях регулирования температуры перегретого пара в смеситель впрыскивается холодная вода. Какое количество воды на 1 кг пара следует подать в смеситель, если через него проходит перегретый пар с параметрами P = 3 МПа и t1 = 480 °C, температуру которого нужно снизить до t2 = 460 °C? Вода на входе имеет давление такое же, как и давление пара, а ее температура tв = 20 °C.
7.39. В трубе течет водяной пар при давлении р = 2,5 МПа и степени сухости Х = 0,98 со скоростью w = 45 м/с. Расход пара G = 6000 кг/ч. Определить внутренний диаметр трубы.
8.ЦИКЛ РЕНКИНА (ЦИКЛ ПАРОСИЛОВЫХ УСТАНОВОК)
Цикл Ренкина является основным (идеальным) циклом паросиловых установок. Характерная особенность паросиловых установок – использование влажного пара в цикле в качестве рабочего тела. Принципиальная схема установки, реализующей цикл Ренкина, представлена на рис. 8.1.
63
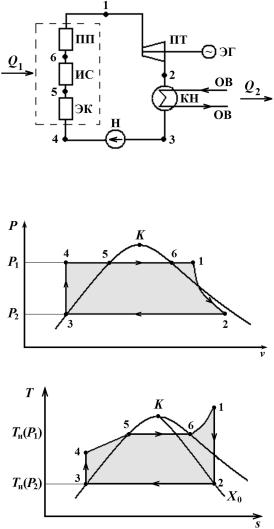
Соответствующие этой схеме v-P-, s-T- и s-h-диаграммы цикла Ренкина представлены на рис. 8.2–8.4.
Цикл состоит из двух адиабат (1-2, 3-4) и двух изобар (4-5-6-1 (P = P1), 2-3 (P = P2)). В области влажного пара каждая изобара является одновременно и изотермой (5-6, 2-3); T1 = Tн(P1), T2 = Tн(P2).
Рис. 8.1. Схема установки, реализующей цикл Ренкина: ПТ – паровая турбина; ЭГ – электрогенератор; КН – конденсатор; ОВ – охлаждающая вода; Н – насос; ЭК – экономайзер; ИС – испаритель; ПП – пароперегреватель; Q1 – подведенное тепло; Q2 – отведенное тепло
Рис. 8.2. Диаграмма v-P цикла Ренкина
Рис. 8.3. Диаграмма s-T цикла Ренкина
64
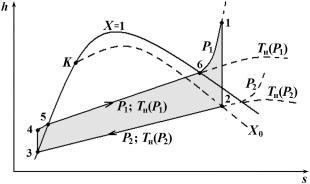
Рис. 8.4. Диаграмма s-h цикла Ренкина
Процессы цикла:
(1-2) – адиабатное расширение пара от P1 до P2; dq = Tds = 0; dh = vdP;
(2-3) – конденсация пара в конденсаторе;
P = P2; T2 = Tн(P2); dh = dq = T2ds;
(3-4) – адиабатное сжатие жидкости в насосе от P2 до P1; dq = Tds = 0; dh = vdP;
(4-5) – подогрев до Tн(P1);
Х5 = 0; P = P1; dh = dq = T ds; T4 ≤ T ≤ Tн(P1); (5-6) – подогрев от X5 = 0 до X6 = 1;
P = P1; T1 = Tн(P1); dh = dq = T1ds; (6-1) – подогрев от X6 = 1 до X1 > 1;
P = P1; T > T1; dh = dq = Tds.
Параметры состояния рабочего тела определяются в точке 4 по таблицам для жидкости в недогретом состоянии (P = P1); в точке 1 по таблицам для пара в перегретом состоянии (P = P1); в точках 3, 5, 6 по таблицам для вещества на линии насыщения; в точке 2 по зависимостям для влажного насыщенного пара (P = P2, T = Tн(P2)). Компактно вся эта информация содержится на s-h-диаграммах.
65
Термический КПД цикла Ренкина
За цикл рабочее тело передает внешней среде в форме работы энергию L1. В свою очередь, внешняя среда передает, а рабочее тело получает в форме работы энергию L2. Разность L = L1 – L2 называется полезной работой цикла. На рис. 8.2 – это площадь, ограниченная кривой цикла 1-6.
С другой стороны, за цикл к рабочему телу подводится от внешней среды в тепловой форме энергия Q1 и отводится Q2 (участки 4-5-6-1 и 2-3, соответственно, на рис. 8.1 – 8.4).
Термический КПД цикла представляет собой отношение полезной работы к подведенной теплоте:
ηt = (L1 – L2)/Q1.
В общем случае (первый закон термодинамики) du = dq – dl. Поскольку внутренняя энергия – функция состояния, то du – полный дифференциал, и за цикл
du = dq − dl = 0.
Следовательно, за цикл Q = Q1 – Q2 = L = L1 – L2 и
ηt = (Q1 – Q2)/Q1.
Ограничиваясь только работой расширения dL = Pdv, получаем du = dq – Pdv, dh = dq + vdP (h = u + Pv; dq = Tds).
Замечательной особенностью цикла Ренкина является то, что подвод и отвод тепла идет на изобарах, где dP = 0. В этом случае dq = dh и, поскольку h – функция состояния, q1 = h1 – h4, a q2 = = h2 – h3, (см. рис. 8.4). Таким образом, термический КПД цикла Ренкина
ηt = (Q1 – Q2)/Q1 = [(h1 – h4) – (h2 – h3)]/ (h1 – h4).
Иногда, пренебрегая потерями энергии на насосе, полагают разность h4 – h3 ≈ 0, тогда
ηt ≈ (h1 – h2)/(h1 – h3).
66
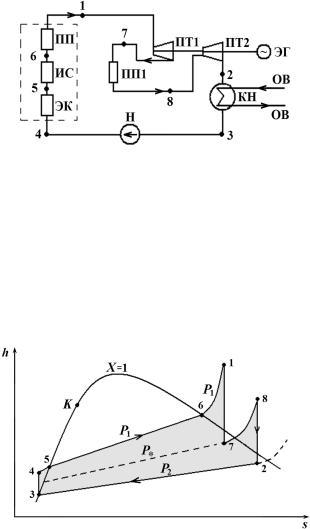
Цикл Ренкина с промежуточным перегревом пара
Принципиальная схема установки, реализующей этот цикл, и соответствующая этой схеме s-h-диаграмма представлены на рис. 8.5, 8.6.
Рис. 8.5. Принципиальная схема установки, реализующей цикл Ренкина
спромежуточным перегревом пара
Вэтой схеме паровая турбина конструктивно разделена на две ступени: ПТ1 (контур «высокого давления») и ПТ2 (контур «низкого давления»).
Отработавший адиабатно на лопатках первой ступени влажный
пар (состояние в точке 7: X < 1; P2 < P* < P1) поступает на промежуточный пароперегреватель ПП1. При том же давлении P* (изобарно) он переводится в перегретое состояние (точка 8) и поступает на лопатки второй ступени турбины ПТ2.
Рис. 8.6. Диаграмма s-h цикла Ренкина с промежуточным перегревом пара
67
Для этого цикла
q1 = (h1 – h4) + (h8 – h7), q2 = h2 – h3
и
ηt = (Q1 – Q2)/Q1.
Если потерями энергии на насосе пренебречь, положив h4 = h3, то
ηt ≈ (h1 – h2 + h8 – h7)/(h1 – h3 + h8 – h7).
Замечание. При решении задач этого раздела используются обозначения рис. 8.1, 8.5 и соответствующих им диаграмм. Рабочее тело (вещество) – вода.
Примеры решения задач
Задача 1. Паровая установка работает по циклу Ренкина. Давление на входе в турбину P1 = 20 бар, а температура 300 °C. Давление в конденсаторе P2 = 0,04 бар. Определить термический КПД этого цикла, пренебрегая потерями энергии на насосе.
Решение
В этом случае (см. рис. 8.1, 8.4), если h4 = h3,
ηt ≈ (h1 – h2)/(h1 – h3).
1.Используя s-h-диаграмму, находим точку пересечения изоба-
ры P1 = 20 бар и изотермы t = 300 °C. Ордината этой точки определяет h1 ≈ 3019 кДж/кг.
2.Опуская вертикаль из точки 1, находим точку пересечения ее
сизобарой P2 = 0,04 бар. Ордината этой точки h2 ≈ 2036 кДж/кг.
3.Двигаясь по изобаре P2 до пересечения ее с кривой фазового
равновесия (X = 0), находим h3 = h′(P2) ≈ 121 кДж/кг.
В итоге ηt = (3019 – 2036)/(3019 – 121) = 0,339.
Определение ηt можно было провести, используя только таблицы термодинамического состояния воды и водяного пара.
Задача 2. В паросиловой установке, работающей при параметрах P1 = 110 бар, t1 = 500 °C, введен вторичный перегрев пара при P* = 30 бар до t8 = 500 °C. Давление в конденсаторе турбины P2 = = 0,04 бар. Определить термический КПД цикла.
68
Решение
Воспользуемся схемой и обозначениями рис. 8.6.
1. По таблицам для воды на линии насыщения находим tн(P1) = = 318,1 °C, tн(P*) = 233,9 °C. Поскольку tн(P1) и tн(P*) меньше
500 °C, то режимы в точках 1 и 8 цикла действительно принадлежат области перегретого пара.
2. По таблицам для перегретого пара находим
h1 |
= h(P = P1, t = 500 °C) = 3362,6 кДж/кг, |
s1 |
= 6,534 кДж/(кг K); |
h8 |
= h(P = P*, t = 500 °C) = 3457 кДж/кг, |
s8 |
= 6,534 кДж/(кг K). |
3. Полагая процессы в турбине не только адиабатными, но и обратимыми (изоэнтропийными), имеем
s7 = s1, s2 = s8.
По таблицам для воды и водяного пара на линии насыщения (X = 0) и сухого насыщенного пара (X = 1) находим
s′(P2) = 0,4224 кДж/(кг K), |
s′′(P2) = 8,4735 кДж/(кг K); |
s′(P*) =2,6456 кДж/(кг K), |
s′′(P*) = 6,1858 кДж/(кг K). |
а) Так как s2 = s8 < s″(P2), то точка 2 цикла расположена в области влажного насыщенного пара (0 < X < 1),
0< X2 = (s2 – s′(P2))/(s″(P2) – s′(P2)) =
=(7,2356 – 0,4224)/(8,4735 – 0,4224) ≈ 0,85 < 1.
б) Так как s7 = s1 > s″(P*), то точка 7 цикла расположена в области перегретого пара (X7 > 1), а не в двухфазной области, как это изображено на рис. 8.6. По таблицам термодинамических свойств перегретого пара для P = P* и s = s1 находим
h7 = 2994,3 кДж/кг (t7 = 300 °C).
4. По таблицам на линии насыщения (X = 0 и X = 1) для P = P2 находим
h3 = h′(P2) = 121,4 кДж/кг; h″(P2) = 2553,7 кДж/кг.
Отсюда
h2 = h′(P2) + X2[h″(P2) – h′(P2)] ≈ 2189 кДж/кг.
69
Исходя из допущения, что s4 = s3 = s′(P2), по таблицам для недогретой (до насыщения) воды при P = P1 и s = s′(P2) = = 0,4224 кДж/(кг K) находим
h4 ≈ 132 кДж/кг.
5.За цикл одним килограммом рабочего тела получена энергия
втепловой форме
Q1 = (h1 – h4) + (h8 – h7) ≈ 3693 кДж/кг,
отдана энергия Q2 = (h2 – h3) ≈ 2068 кДж/кг. Отсюда искомый термический КПД цикла
ηt = (Q1 – Q2)/Q1 = 0,440 = 44 %.
Замечание 1. Если положить h4 = h3, это приведет к увеличению Q1 на величину h = h4 – h3 ≈ 12 кДж/кг. При этом получим η*t = = 0,442 = 44,2 %, (η*t – ηt)/ηt = 0,0045 < 0,5 %.
Замечание 2. Значения термодинамических параметров в точках 6, 1, 7, 8 и 2 цикла легко определить по s-h-диаграмме.
Задачи
8.1.Паротурбинная установка работает по циклу Ренкина при следующих параметрах пара на входе в турбину: P1 = 90 бар и t1 =
=535 °C; давление в конденсаторе P2 = 0,04 бар. Определить внешнюю работу турбины и питательного насоса, а также термический КПД цикла с учетом и без учета работы насоса и относительную разность этих КПД
8.2.Паротурбинная установка работает по циклу Ренкина с
начальными параметрами: P1 = 100 бар и t1 = 530 °C; давление в конденсаторе P2 = 0,04 бар. Определить термический КПД цикла и сравнить его с термическим КПД цикла Карно в том же интервале температур.
8.3. Определить, какова должна быть температура пара перед входом в турбину, если его давление P1 = 100 бар, давление в конденсаторе P2 = 0,04 бар, а влажность на выходе из турбины не должна превышать 15 %. Задачу решить по таблицам.
70
