
Vakarchuk_I_O_Kvantova_mehanika_Pidruchnik_B
.pdfäå åíåð iÿ |1si-стану E1s = −e2/2aB, кулонiвський iнте рал
K = |
Z ϕ1s(rA) |
e2 |
− |
e2 |
|
ϕ1s(rA) dr |
||||||||||||
R |
rB |
|
||||||||||||||||
|
|
e2 |
|
|
|
|
|
e2 |
|
|
|
|
||||||
îáìiííèé iíòå ðàë= |
|
|
|
− Z |
ϕ12s(r) |
|
|
|
dr, |
|||||||||
|
R |
|r + R| |
||||||||||||||||
|
Z ϕ1s(rA) |
e2 |
|
|
e2 |
|
ϕ1s(rB ) dr |
|||||||||||
A = |
|
− |
|
|
|
|||||||||||||
R |
rB |
|
||||||||||||||||
|
|
|
e2 |
|
|
|
|
|
|
|
|
|
e2 |
|||||
Другi рiвностi в = |
S |
|
− Z |
ϕ1s(r − R) |
|
ϕ1s(r) dr. |
||||||||||||
R |
r |
|||||||||||||||||
руванняозраху.а¹мосьвеличиниK розкладомтA отриму¹мо шляхом замiни змiнних iнте
т . Скорист |
|
|
|
|
|
|
S, K, Aряд.ПочнемоФур'¹: з iнте рала перекрит- |
|||||||||||
Фур'¹- ункцiямпоненту |
|
ϕ1s(r) = |
1 |
X |
ϕq eiqr. |
|
||||||||||||
|
|
|
|
|||||||||||||||
|
|
|
|
|
||||||||||||||
V |
q |
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Ÿ82, äå |
|
|
ϕq |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
обчислюваласьзнахвiдповiднадимопростимкомпонентаповтореннямдляункцi¨викладок |
|||||||||||||||||
тобто |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ϕ2 |
(r), |
|
ρ1s(q): |
|
|
|
|
|
|
|
|
|
|
|
1s |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
κ4 |
|
|
|
|
|
||
Тепер |
ϕq = 8qπaB3 |
|
|
|
, |
|
κ = 1/aB. |
|
||||||||||
(q2 + κ2)2 |
|
|
||||||||||||||||
|
|
|
1 |
X |
1 |
|
X |
|
|
|
Z eiq1reiq2(r+R)dr |
|
||||||
|
S = |
|
V q1 |
V |
q2 ϕq1 ϕq2 |
|
||||||||||||
Ми використали= |
1 |
X X |
|
|
q2R |
δплоских. хвиль: |
|
|||||||||||
òóò ортонормованiстьϕ ϕ e |
|
|||||||||||||||||
|
|
|
V |
|
q1 |
q2 |
|
q1 |
q2 |
|
q1,−q2 |
|
||||||
692 |
|
|
|
|
|
|
|
|
|
1 |
|
Z |
ei(q−q′)rdr. |
|
||||
|
|
|
|
δq,q′ = |
|
|
|
|||||||||||
|
|
|
|
V |
|
|||||||||||||
Тепер |
|
|
|
|
|
|
|
|
Z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(q |
|
|
|
|
+ q0 ) проведенiaB |
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
e2 |
|
|
|
|
|
X |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
4πe2 |
|
ρ1s(q)e qR, |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
äå |
|
|
|
|
|
|
|
|
K = |
|
|
|
− |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
R |
V |
|
q |
|
q2 |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
iqr |
|
|
|
|
|
|
|
|
|
|
|
|
|
q04 |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|||||||||
|
|
ρ1s(q) = ϕ1s(r)e |
dr = |
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
|
|
q0 = |
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
2 |
|
|
|
|
|
2 2 |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
леннiбуло знайденоiнтералав перекриттяŸ82.Повторюючи викладки, |
|
|
|
при обчис- |
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
S, ìà¹ìî: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
e2 |
|
|
2e2 |
|
|
∞ sin qR |
|
|
|
|
|
|
|
|
|
|
|
|
e2 |
|
|
|
|
|
e2 |
|
|
|
|
|
∞ |
1 |
|
|
|
|||||||||||||||||
K = |
|
|
− |
|
|
|
Z |
|
|
|
|
|
|
ρ1s |
(q) dq = |
|
|
|
|
|
− |
|
Im Z |
|
eiqR |
|
|
ρ1s(q) dq |
|||||||||||||||||||||||||
R |
|
π |
|
qR |
|
|
|
|
R |
πR |
q |
||||||||||||||||||||||||||||||||||||||||||
|
|
|
− πR |
0 |
Z |
|
|
|
|
|
|
|
|
|
|
|
|
Z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
−∞ |
|
|
|
|
|
|||||||||||||
|
R |
|
|
|
|
|
|
|
|
q |
|
|
|
|
|
|
|
|
|
|
|
|
q |
|
|
|
|
|
|
− |
|
|
|
|
|
|
|||||||||||||||||
= |
e2 |
|
|
|
e2 |
|
Im ∞ |
eiqR |
dq + |
|
∞ |
eiqR |
|
[ρ1s |
(q) |
|
1] dq |
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
−∞ |
|
|
|
|
|
|
|
|
|
|
|
−∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
e2 |
|
|
|
e2 |
|
|
∞ sin qR |
|
|
|
|
|
e2 |
|
|
|
|
|
|
|
|
∞ eiqR |
|
|
|
|
|
|
|
q04 |
|
|
|
|
|
|
|
|||||||||||||||
Îñêiëü= êè ïåðøèé iíòå ðàdqë äîðiâíImþ¹ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
dq. |
|||||||||||||||||||||||||||||||
Z |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
R |
|
− πR |
|
Z |
q |
|
|
|
|
|
|
|
− |
πR |
|
|
|
q |
|
(q2 + q02)2 − |
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
−∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
−∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
нiй доданок: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
π, залиша¹ться лише остан- |
||||||||||||||||||||||||||
|
|
|
e2 |
|
|
|
∞ |
iqR q3 + 2qq02 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
K = |
|
|
Im Z−∞ e |
|
|
|
|
|
|
dq |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
πR |
|
|
(q2 + q02)2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
e2 |
|
1 d |
|
∞ |
iqR |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
q2 |
|
|
dq |
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
||||||||||||
= |
|
|
Im |
|
|
|
Z−∞ e |
|
|
|
|
|
+ |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
πR |
i |
dR |
|
|
|
q2 + q02 |
(q2 + q02)2 |
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
e2 |
|
1 d |
1 |
|
|
|
|
|
|
|
d |
|
|
|
|
|
∞ |
|
|
eiqR |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
= |
|
|
Im |
|
|
|
− q02 |
|
Z−∞ |
|
|
dq |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
πR |
i |
dR |
dq02 |
q2 + q02 |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
e2 |
|
1 d |
1 |
− q02 |
d |
|
|
π |
e−q0R = |
e2 |
1 + |
q0R |
|
e−q0R. |
||||||||||||||||||||||||||||||||||||
694 = |
|
|
Im |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
πR |
i |
dR |
dq02 |
q0 |
R |
2 |
|
|
||||||||||||||||||||||||||||||||||||||||||||
Таким чином, остаточно кулîíiвський iнте рал
|
|
|
|
|
|
|
e2 |
(1 + ρ)e− |
2ρ |
. |
|
|||||||||
рядЗвернiмосьФур'¹величинудообчисленняK = R |
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
обмiнного iнте рала. озклада¹мо в |
||||||||||||
Îòæå, |
|
|
|
|
e2 |
|
|
|
e2 |
1 |
|
e−r/aB . |
||||||||
|
|
|
|
|
ϕ1s(r) = |
|
|
|
|
|
|
|||||||||
|
|
r |
r |
q |
|
|
||||||||||||||
|
|
|
|
πaB3 |
||||||||||||||||
|
e2 |
|
e−r/aB |
1 |
|
|
|
|
|
e2 |
|
|
4π |
|||||||
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
eiqr, |
|
|
|
|
|
|
r |
V |
|
|
|
|
|
|
|
|
q2 + κ2 |
|||||
3 |
|
|
|
|
|
|
|
|
|
|
3 |
|||||||||
|
qπaB |
|
|
|
|
|
|
|
X qπaB |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
q |
|
|
|
|
|
|
|
|||
1
Далi перетворення, подiбнi доκ ïî= ïåð.еднiх, дають:
aB
|
|
|
|
|
|
|
e2 |
1 |
X |
eiqRϕq |
|
|
|
|
e2 |
|
|
|
|
|
|
4π |
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
A = S |
|
− |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
R |
V |
|
|
|
|
|
|
|
|
|
|
|
q2 + κ2 |
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
qπaB |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
q |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Iíòå ðàë |
|
|
= |
|
S |
e2 |
− |
|
e2 |
|
|
|
Im Z |
∞ |
|
eiqR |
|
|
|
qϕq |
|
|
|
dq. |
|||||||||||||||||||||
|
|
|
R |
|
|
|
|
|
|
|
|
q2 + κ2 |
|||||||||||||||||||||||||||||||||
|
|
|
Rπ πa3 |
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
q |
B |
|
|
|
|
|
|
|
|
−∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
κ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
κ |
|
|
|
|
|
|
|
q |
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
κ |
|
|
|
|
|
|
|
||||||||
∞ |
|
qϕq |
|
|
|
|
|
∞ |
|
|
|
|
|
|
|
q |
|
|
|
|
|
|
|
|
8 πaB3 κ4 |
|
|
|
|||||||||||||||||
eiqR |
|
|
|
|
|
dq |
= |
|
|
|
eiqR |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dq |
|||||
|
2 |
|
|
2 |
|
|
|
|
2 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
2 |
|
|
|
|
|
2 |
2 |
|||||||||||||||
Z−∞ |
q |
+ |
|
|
|
|
Z−∞ |
|
|
|
|
q |
+ |
|
|
× (q |
+ |
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
) |
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
d |
|
|
|
|
|
d |
|
|
2 |
|
|
|
|
∞ |
|
eiqR |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
= −i4κ4qπaB3 |
|
|
|
Z−∞ |
|
dq |
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
dR |
dκ2 |
q2 + κ2 |
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
d |
|
|
|
|
|
d |
|
|
2 |
|
π |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
= −i4κ4qπaB3 |
|
|
|
|
|
|
|
e−κR |
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
dR |
dκ2 |
κ |
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
= iπq |
|
e−κR[κR + (κR)2]. |
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
πaB3 |
|
|
695 |
||||||||||||||||||||||||||||||||||
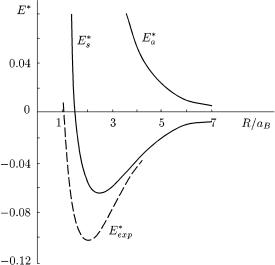
|
ðiâíþ¹ |
сперимент. |
|
|
|
|
ис. 70. Електроннi терми йона водню H+ |
|
|
|
|||
ëâiдповiдаютьнiя знакам плюс т |
мiнус у загальнiй.Суцiльнi кривiормулiE. (ШтриховаR), E (R) |
|||||
|
|
|
2 |
|
s |
a |
|
|
|
|
|
|
|
ä |
Eexp |
|
|
|
íàñëiäîê, |
|
|
|
|
|
|
||
|
|
симетричною:спiн ваядкузмiннадлянабува¹спiново¨лишеункцi¨два значення, то ви |
||||
значник третьогодорiвню¹1/2 |
|
|
|
|
||
|
|
|
|
|
|
- |
îинатомопжносисмувнiстюжуситьемаперебуватибути¹нестабiльноюантисимнулевiовалентний.центрiОтже,длятричною,.Цемiжднi¹¨просторовапричиноюусiмазцепарознача¹,ядрамипросторовихункцiятого,i,щощоякнеелектрониможзмiннихбу |
||||||
тневак |
|
|
χσ1 |
σ2,σ3 (s1 |
s2, s3) |
|
|
|
|
|
|
|
екули |
|
|
|
|
|
дома¹ власти |
|
|
|
|
|
щомолеку, |
|
|
Hâiñòü3 ненасичену¹.Тобтоя.У нашомук прикладiзв'язок,цеознаякбачим¹, |
|
|
||||
|
неасиченволодiлиможладенихмалиякпiд'¹довалентспiном,цiлийатискспiногоажiмо,атомзв'язкубулиHбозеiнеутворитимала-насиченбiльшихтинками,мця. тоЯкщооваленлу H б. |
|||||
електроЯкбиивiсть2 вжелектрони |
|
|
|
3 |
||
|
|
|
|
|
|
- |
|
|
запереченьнасталащоб ,äтоляiснуванняiñтьмолекуомплексiв,H |
||||
зокреманогозв'язви |
у бу б,вищево |
3/2 |
|
|
|
|
íå áóëî á. |
|
|
|
|
6973 |
|

напрямленостi.доПочнемоiншо¨ х онкретного приклхiмiчногоду утзâ'язкурення молейого
êовутакою:лиПерейдемоамiакуномелектрониNHуаблицi.Електроннасуперпозицi¨,елементiварактеристикиондорiвню¹i урацiя7)àтомавосназотуному(порядстанi |
||||||||||||||||||||||
¹ |
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
2 |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
кутовимаютьзв'язку |
||
ñòàíi, äâà(1s) (2s) (2p) |
тобто два електрони перебу |
1s |
||||||||||||||||||||
вСамеомбiнацi¨моекулi NH |
|
é âiä |
овiдають2s- анi затриутвоелектрониенняхiмiчного2p-ñòàíi |
|||||||||||||||||||
ïîäië ì, ÿêèé3зада¹ться.Електроннiсеричнимивихiднiани ункцiямиизуються |
ðîç- |
|||||||||||||||||||||
|
|
|
прц хнципомункцiй |
|
|
|
|
|
|
|
мианиможемовзяти Y1,0, Y1,1 |
, Y1,−1 |
||||||||||
êÇãiäí |
ç |
|
|
|
|
|
çà |
|
|
|
|
|
|
|
|
|
|
|
|
утворитиакi: лiнiйнi. |
||
|
|
|
| xi |
|
|
|
|
√ |
|
|
|
|
|
r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
π |
|
|||||||||||||
|
|
|
|
|
|
|
2 |
|
|
|||||||||||||
|
|
|
ëi |
= |
|
|
óíêöi¨ |
|
|
3 cos ϕ sin θ, |
|
|||||||||||
|
|
|
p |
|
Y1,−1 − Y1,1 = |
|
|
|
||||||||||||||
|
|
|
|
|
|
|
Y |
|
|
+ Y |
1,1 |
3 |
|
|
||||||||
|
|
|
|pyi |
|
= |
− |
|
1,−1√ |
2 |
|
|
= r |
4π |
sin ϕ sin θ, |
|
|||||||
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
||||
|
вженабуваютьутворюватибговорювалинапрямцi овалентнийосейŸ41. Максимальнi з |
чення |
||||||||||||||||||||
вониМи |
|
|pz |
|
= |
Y1,0 = r 4π cos θ. |
|
||||||||||||||||
|
òьсянах |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
íêàæóóцихвать,- |
|
ñïàðþ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
¹ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
атись,молекужз електрономдню. iншого x,атомаy, zзв'язок,.тКоженсамо,або,електроякякцевiдб |
||||||||||||||||||||
698 |
ис. 71. Молекула амiаку. |
зв'язкахелектронамиовалентнiхункцiй,витягнутзв'язки,трьохякi вздовжà¹томiввiдпомолекуâдоiднимилiцiатнихюводнютри. Хвильовiлipнапрямкiв-.станиiйниЕлектроннiиутворюютьункцi¨,омбiнацiямиосейхмарищоопзв'язкинасуютьтомцихз-
У молекули амi ку NH3
нююласнеорму.71)ь пiрамiдине.Причому90.чимо,Однакякпоказу¹кутидосвiд,мiж напрямкамимолекула амiакуцихзв'язкiвx,справy, zä(диворiвма¹-.
âяканняiдшÎòæпростороваовхуваiвiдповiденерме,навизнiжякпоняттiпринципомi¨мiнiмумом.бача¹ться.апряо¨силiнiйно¨ленiстьетрiнапрямленiстюхiмiчнiсуперпозицi¨,¨¨повно¨.кСтiйкiстьомбiнацi¨.зв'язкиТенерчи)симетрi¹ювнаслiдокiншаi¨конхiмiчниххвильовихмають.Тутнеспаренихпоняттiструктураурацi¨зновумiжелектронногоакузв'язкiвпринципомпростежу¹молекулиункцiйвластивiсть,електронiвмолекули.Вгадурунìçà- |
|||||
нiмумузв'язокбезпечу¹тьсту¹ться |
◦, |
äåùî áiëüøi ( 107◦ |
|
||
Êiëüê ñòü |
жливих зв'язкiв, тобто |
я валентностi ¹ |
|||
ä ñ òü |
зиваю ь його ва ентнiстю. Саме |
||||
простим. Зокрема, |
валентнiсть мож |
абувати дро |
|||
атома,б вèх значень, як наприк |
äëÿ |
елементiв у |
|||
ðÿäi ñï |
|
. |
|
|
|
|
îëперекриванняукулiомднаоазотудногохвильовихNзiй(наприклад,ма¹моямкiв,унрiдкiсноземельдецiйладцеелектроннiелектронiвкратностiнапрямокхмарихiмiчнихосiрiзнихвитягнуатомiвзв'яз |
||||
тiазотукiвназустрiч.УПерекривамвздовж |
2 |
|
|
||
ютьним, що да¹ великакимчення обмiнно¨ енер i¨. Цей зв'язокz), íàç¹ñèëüâà
|
|
|
|
|
- |
çв'язкутим,-зв'язк,щоцьомунапрямкивипадку.Удвоххвильовихак(вздiншихсимумiввжосейрозподiлуямкункцiйах,перпендикулярних¹меншимгустини.Цеелектронпов'язанодо |
|||||
õìàðσ |
|
|
|
σ |
|
дного. Отже, цi, як ¨х називають,т |
y |
) ¹ ïàðà |
ельними |
|
|
роннудо |
x |
|
|
|
|
çâ'ÿçê |
π-çâ'ÿçêè |
ëàáøi ïîðiâíÿ |
|||
ñèñêõiìi÷íîþσ):-зв'язк¹сильним,омрмулою,.Тдвачином,деiншiзв'язокслабшимимолекулiпознача¹тьс.азотуЧастрискоюîдинцезобрпотрiйн(вàлентжа¹тьèõà-
участюозгконляньмоN атома≡iNурацiю.щевуглецюядцiкавих.Iзольованийприкладiватоммолекувугëецюярнихма¹утворелектíü
(1s)2(2s)2(2p)2, як вiдповiда¹ двовал нтно699-
ìó |
|
. Однак вуглець |
|
хiмiчних сполуках виявля¹ вале т- |
||||||||||||
вуглецюнiсть,атомуяк перехдорiвню¹дитьчотирьомутворюватзбуджен.Цейознача¹,повно¨щодин iз sелектронуiв- |
||||||||||||||||
гiбридизацi¹ю |
|
|
|
|
|
|
|
p-ñòàí i ìè ìà¹ìî |
|
|
|
|||||
êîí i óðàöiþ |
|
|
|
|
|
|
|
|
íó |
|||||||
|
|
|
âiðíîñ |
|
|
|
|
|
|
|
|
|
|
|
||
трьом |
|
|
(1s)2(2s)1(2p)3, яка дозволя¹ дному s- |
÷îìó çáiëü |
|
|||||||||||
|
|
|
|
|
|
|
|
пониждiхiмiчнiелектроназв'язкиiз. Пр |
|
|||||||
шення pенер-еле i¨тронаматома при перех |
|
|
|
|
|
|
||||||||||
íèé |
|
|
|
|
суперпозицi¨, |
|
sназива¹тьс-стану збудже |
|
||||||||
|
Ïiñëÿ |
|
|
|
|
|
гiбридизацiй |
|
||||||||
|
|
|
компенсу¹тьсяхiмiчного зв'язкуеннямутворюватисполуках. еIзерцихi¨ причотирьутвох |
|||||||||||||
ðåííióíêöiép-астаномами |
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
заб зпечуватиможнамiiмум процедураенерi¨ сполуклiлiнiйнiахкомбiнацi¨.Нагцi¨,да |
|||||||||||||
¹мо,якi щоббудуть|s , |px |
, |py , |pz i |
|
|
|
|
|
|
|
|
|
||||||
складовихЗгiдностак,омбiнацi¨анiвТутбулиз |
|
|
|
|
√ |
|
. Такелектрона |
|
ÿ 3 |
|
||||||
Надалi, |
|
|
(наприклад,áiíàöi¨ |
|
|
|
|
Yl,m(θ, ϕ) |
||||||||
|
|
потрiбнопринципомiм.зТобтоповнихднаковимиелåкзробункцi¨хвильовихроннiперебування.хзауваженнястанiвункцiй,.миУтворимоповинприалiнiйнiнеïîòðiáíîööiâèутворюватишеповогожномуз¨хнiхкарактерукутовихлiнiйнiнових-. |
||||||||||||||
|
|
|s = Y0 0 |
= 1/ 4π |
|
|
|
|
|
sp |
|
||||||
Y1,1(θ, ϕ) |
|
|
|
|
|
êöiþ R2,1(r) |
çàìiñòü |
|
|
|||||||
çöi¨íà |
вiдпо¹днаковимиiднiрадiальнi |
хвильовiутворю¹моункцi¨. Якщо радiальнiкомбiнацi¨домножуватилишеунк |
||||||||||||||
|
|s |
|px |
|py |
|pz i |
|
|
|
|
||||||||
|
анiв), толiнiйнiвиносиì |
¨х як тiлькиспiльнийзкутовихмножникчастинзадужки, i за- |
||||||||||||||
ëèøp-стються |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
розумi¹моне вв дячинi вих |
|
значе |
ь, пiд величинами |
|
|
|
. |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|s |px , |pyi, |
|||
частину |
íà âiäïîâiä |
радiальнiхвильвi ункцi¨кцi¨,. тобтоНаприклад,добуток |
¨х кутовихза |
|||||||||||||
|pz i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|2px |
пишемо просто |px |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
- |
ано¨ вище Наприклад,лiнiйно¨омбi |
|
|
пам'ята¹мо,серичних щоункцiйце¹добутокY (θ, ϕ)ïèà |
|||||||||||||
них анiвнацих.радiальнузауваженьпершийуперех димоновийдостан.утворення |
1,−1 |
|
- |
|||||||||||||
Унаслiдок того, що|1i = C |si + |pxi + |py i + |pz i . |
|
|
|
|
||||||||||||
|
|
|
|
|
|
s- òà p-стани ¹ ортогональними мiж собою, |
|
|||||||||
|
|
|
|
|
|
hs|pxi = 0, hpx|pyi = 0, |
|
|
|
|
||||||
|
|
|
|
|
|
hs|py i = 0, hpx|pz i = 0, |
|
|
|
|
||||||
700 |
|
|
|
|
hs|pz i = 0, hpy|pz i = 0, |
|
|
|
|
|||||||
|
|
|2 |
пiдберемо так, |
щоб вона мала тi ж властивостi й була |
||||||||||||||
|
|
|
знаквикористовуючи+ перед h1|2 |
=ìî0. |
Наступнiпершийäâi óíêöi¨ðàç |3 ñòà |4i |
|||||||||||||
içiсцямизнаком |
|
|
|
|
|
äâi |
жливостi: |
|
|
|
ïîìiíÿ¹ìî |
|||||||
|
|
|pz i iç знаком − ïå |
|
|
|py i |
|||||||||||||
зкцiюумови нормування h1|1i = 1 знаходимо C = 1/2. Наступну н- |
||||||||||||||||||
ортогональною до |1i: |
|s − |px |
− |py + |pz |
. |
|
||||||||||||||
знайдемо,Легк переконатись,|2i = 2 |
|
|||||||||||||||||
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ùî |
|
|
|
|
|
|
|
|
|
|
|
|
|
ають такий− вигляд:перед|pxi. Остаточно чотири о |
едтонормованих, другий раз |
|||||||||||||||||
|
|
|
àíè |
|||||||||||||||
|
|
|
|
|1i = |
1 |
|
|si + |pxi + |py i + |pz i , |
|
||||||||||
|
|
|
|
|
|
|
||||||||||||
îñÿì |
|
2 |
|
|
||||||||||||||
|
áiëÿ |pi |
|
|
|
iâ |
|
|
|
|1i |
|
|
|||||||
|
|
|
|
|2i |
= |
2 |s |
− |pxi − |py i |
+ |
|pz i , |
|
||||||||
|
|
|
|
|
|
1 |
|
дiагоналi |
|
|
|
|
|
|
||||
|
|
(x, y, z), äðóã é ñòàí |2 |
|
|
апрямку |
дiагоналi октанта, |
||||||||||||
|
|
|
|
|3i |
= |
2 |
|
|si − |px |
|
+ |py i − |pz i , |
|
|||||||
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
ùî |
|
|
îñÿìè (−x, −y, z).дiлуСтан |3 |
|
|
|
ямлений уздовж |
|||||||||||
|
|
|
|
напрямки|4 =зв |
2 |
|
|s |
+ |px |
|
− |py i − |pz |
. |
|
||||||
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
ОсВизначимоiльки |
òîìiâ |
|
'ÿзкi , що утворюютьсянапрбазi цих станiв. |
|||||||||||||||
ристрону |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|||
ються знаками|si-ñòàí ¹ ñ åðè÷ |
|
-симетр чним, то |
|
|
ямки изнача- |
|||||||||||||
|1i, | , |
|3 , |4 |
|
|
|
|
|
|
|
|
îðáiò |
|
|
утвореного |
|||||
ìàêутворениймумом у напрямку- |
|
|
. Першийпершогостан октх рактеризуютьсянта, |
|||||||||||||||
|
îðáiòàëi |
|
õiìi÷íèé |
|
|
|
|
|
|
|
|
|||||||
|
|
72) |
|
|
(−x, y, −z), |
|
|
|
молеку4ëàõ C(реону3 4 |
|||||||||
ютьдiагоналi октант |
ñòàí |4i напрподiагоналi октан |
|||||||||||||||||
мiститипрямленi(x,тетраедричну−y,àòîì−zäî).вуглецю,Макершин |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
структуруимумитетратомаксимумирозпо.драТбто.Томуякщоелекгучотиристинвронцеелектронниххвильовiхмартетраедраутворюункцi¨хмарпо |
|||||||||||||
|
|
|
|
|
дню,чотирьотьтоотрима¹маютьелектронiваеднимиìîмолекуналицихCClлуямиорбiтмет.Якщоаляхнупопiд'¹делек(див. |
|||||||||||||
íàти. довiд.Ткакужногоутворюютьназиваструктуру |
|
|
|
|
|
|
|
|
|
|||||||||
æ |
|
|
|
|
|
|
|
|
|
|
çâ'ÿçîê |
|
|
|
|
CH ). .Îñ701Öi- |
||
