
Vakarchuk_I_O_Kvantova_mehanika_Pidruchnik_B
.pdf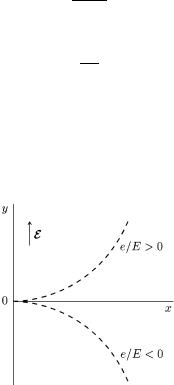
|
|
|
ðiâíy = 2mE t . |
|
|
|
|
|
|
|||||||
|
|
|
|
|
e |
|
|
|
|
|
|
|
|
|
||
Виключимо час i знайдемо |
|
|
ÿííÿ2 òðà¹êòîði¨ |
|
|
|
|
|||||||||
Запишемо його через початковуy = |
|
E |
x . |
частинки |
|
|
|
|||||||||
|
|
|
|
|
eåíåð2iþ |
|
|
|
|
|
|
|||||
|
|
|
|
|
2mv2 |
|
|
|
|
|
|
|
|
|
||
|
|
|
y |
ðiþ= |
E x |
|
. |
|
|
E = mv2/2: |
||||||
|
|
|
|
|
|
ç äîä òíîþ |
|
|||||||||
|
|
|
|
|
e |
|
|
2 |
|
|
|
|
|
|
|
|
i¹юЯкщо розглянути тра¹кт |
|
|
руху частинки |
|
|
|
åíåð |
|||||||||
|
|
|
|
|
4E |
|
|
|
|
|
|
|
|
|
||
ç òðà êòîði¹þ |
|
|
|
î заряду |
|
= |e|, точастинки,вбiга¹ться |
||||||||||
E = E+ |
iдляздодатнимвiд'¹многзарядом e+ |
|||||||||||||||
íó åíåð iþ |
|
|
|
|
|
|
|
|
|
e− = −|e| |
ÿ é ì๠âiä'¹ì- |
|||||
E = E− = −E+ |
|
ðà¹êòîðiÿòðà¹êòîði¹þ |
|
iз зарщоядома¹e |
||||||||||||
протилежнийi вiд'¹мною енерзарядi¹ю збiга¹ться. А |
|
|
|
|
|
частинки |
|
|
|
|||||||
|
(−e) äîäàòну енер iю. Це iлюстру |
ðèñ. 61. |
||||||||||||||
ис. 61. Класична тра¹кторiя руху |
|
|
|
в електрич |
|
ïîëi. |
||||||||||
Другий приклад це рух заðядже о¨ частинки в однорiдному |
||||||||||||||||
магнiтному полi напруженостi H. частинкиiвяння руху: |
|
|
|
|||||||||||||
Îñêiëüêè |
|
|
p˙ = e |
[vH]. |
|
|
|
|
|
|
||||||
|
|
|
|
|
c |
|
|
|
|
|
|
|
|
|
|
|
v = const, то з виразу |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
p = |
|
|
|
mv |
|
|
|
= |
E |
|
|
|
|
||
592 |
|
|
|
v |
|
|
|
|
||||||||
p |
|
c2 |
|
|
|
|
||||||||||
1 − v2/c2 |
|
|
|
|
||||||||||||
знаходимо
шенняЗнову ми бачимо, що закониv˙ |
=ð |
ec |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
õó[vзалежатьH]. |
лишеспостережувальностiвiдзнаквiдно |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
E |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
e/E: тобто рух |
âiä'¹ìíîþ åíåð i¹þ öå ðóõ |
|
арядом |
|||||||||||||||||||
(íîþ−eÎòæå,).åíåð |
|
|
|
|
|
|
таку iнтерпретацiю |
|
|
гiпотезу |
|
|||||||||||||
|
|
|
ìèi¹þ æåìî äàòè |
|
|
|
|
|
|
|
|
|
|
äëÿ |
íiâ âiä'¹ì |
|||||||||
перед |
|
|
E− |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
- |
÷ÿêàермiпринципомдостщоПiсляинакатною-дочастинки,енергоприродицихзздодатноювiд'¹мноюi¹юенерануПаулi,попереднiхзайнятi.i¹юакi,вакуумуˆхiзичного¹енерможна¹лишеякенервiльнчастпростихеле.Вакуумуi¹ю,ркуваньЩi¹ю,розглядатиднатрони,мизайнятi,алебстору,ами.ДiракчасуникнутипитПричзсСловапротилежнимто(минкормуувiвякомуреяк.кпролю¹моМиДiрака),жномуякщоозначенняани,всiзновумовазарщоанi,ядомопинилисьниописуютьвсiвакуумуйдеiззгiдн.Дiравiд'про |
||||||||||||||||||||||||
ç¹ìíîþ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
а¹мницею |
|
äè |
|
|
|
|
|
|
. |
|
|
|
|
|
òå, ùî âñi |
ç |
||||||
вiд'¹мними |
наченнями нер i¨ |
|
|
|
|
¹ íå áiëüøå íiæ |
закли |
àí- |
||||||||||||||||
ня, оскiльки виника¹прирояд |
|
|
|
|
|
|
àíü ïðî |
|
|
|
|
åíåð iþ, |
||||||||||||
áåçì æíèé |
|
ÿä, ñòiéêiñ ü i |
|
.ä. ÿêi çà |
шаютьсябезмежнувiдпо iдi. |
|||||||||||||||||||
Îòæå, дух По ожнечi |
íå ò |
|
|
просто схопити . |
|
|
|
|
|
âàí- |
||||||||||||||
|
ßêùî ïiä äi¹þ çîâí øíiõ ñèë îäèí |
|
електронiв здiйсню¹ |
|||||||||||||||||||||
товий перехiдзар моря Дiракакв |
|
зайнятi |
|
5 |
|
|
|
|
|
|
||||||||||||||
|
стани додатно¨ енер i¨, то |
|||||||||||||||||||||||
ç додатí |
þ åíåð i¹þ |
|
додатним зарядом (див. рис. 62). |
|
частинку |
|||||||||||||||||||
âiëüíå |
èé ñòàí ç iä'¹ìíîþ åíå |
|
i¹ю поводить себе як |
|
à |
|||||||||||||||||||
Дiрак ототожнював |
цi стани з протонами. За його словами,Спочату ой |
|||||||||||||||||||||||
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ìå iñòî åëü: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
. . . Ти зна¹ш жах порожнявих просторiв |
|
|
|
|
|||||||||||||||
|
|
|
|
Фауст:I вiчне безгомiння самоти? |
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
. . . Я й сам незгiрше знавсь на тому |
|
|
|
|
|||||||||||||||
|
|
|
|
|
Вивчав пусте, навчав пустому, |
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
I |
пильнiш заглиб |
ювався в рiч, |
|
|
|
|
|
||||||||||||
|
(É.- |
|
|
Òùîáiëüøå â íié |
являлось |
протирiч. |
|
|
|
|
|
|||||||||||||
|
. €ете Фауст . Переклад М. Лукаша.) |
|
|
|
|
|
|
593 |
||||||||||||||||
38 I. Î. |
Вакарчук |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
÷àñ íå àê |
|
|
áóëî |
|
як тепер, на нову части ку, |
|||||
виному |
|
легкорiя ¹ симетричною стосовно частинок з |
âiä'¹ìíèì |
|||||||
додатним з |
|
|
|
i,наважитись,умку Дiрака, |
|
þ ñïî |
||||
|
âií îáåð |
æíî ïiäõ äèâ |
iнтерпр |
цi¨ дiркових станiв. оз |
||||||
тережувану |
|
|
|
властивостей електрона |
ïðîòîна могла |
|||||
áóòè |
ìiæ |
|
|
|
|
äiÿ. Äiðàê |
св домлював ¨¨ недостат- |
|||
мати масуелектротрокращеí . Так Дiрак теоретично вiдкрив позитрон. |
||||||||||
нiсть для пояснеасиметрiюядами,íí ако¨ велико¨ рiзницi ¨хнiх мас |
завершив |
|||||||||
Oxford, 1930) словами: |
жливо, що усунутивiдповiдальнцю трудн сть мож |
|||||||||
ñâîþ |
êíèæ |
ó (P. A. M. Dira . The prin iples of quantum me hani s. |
||||||||
áóäå òîäi, |
îëè |
|
вза¹мозумiтимемо природу вза¹модi¨. Пiзнiше |
|||||||
. Вейль з мiр ува ь |
симетрi¨ |
показав, що ця частинка повинíà |
||||||||
|
|
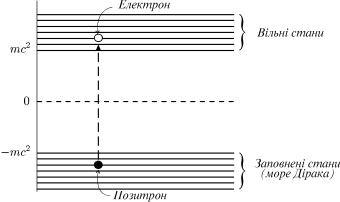
ис. 62. Енер етичний спектр релятивiстсько¨ част нки. |
||||||
|
|
Експериментально позитр |
виявив американський |
içèê |
||||
К. Д. Анде сон у 1932 роцi в к смiчних променях. Вивчаючи о |
||||||||
ють додатний |
заряд. Тим часом К. Д. Андерс н, маючиотiвäíó î |
|||||||
ãðà i¨ |
камери Вiльсона, вiн помiтив аномальнi треки части |
|||||||
íî |
|
iз масою, |
îþ äî |
си електрона |
додатним елемен |
|||
арним |
зарядом.близькЦi аво, що англiйський iзик П. Блекетт |
|||||||
великуамери Вiльсонотогра, не зiйне¨, тобто, що цi частинки справ |
i |
|||||||
|
|
|
ñåðiþ |
з т кими треками, але вiн х |
îâåñ |
|||
|
строго, що це ч стинки, |
ямок руху яких спрямова ий до |
||||||
тогра iю, |
з американською прагматичнiстю |
оголосив свiй винмав- |
||||||
594 |
|
|
|
|
|
|
|
|
хiд i отримав у 1936 роцi Нобелiвську премiю за вiдкриття |
|
|
|
||||||||||||||||
òðî . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
¨õ |
||
датнимиклад, акий перехiд можелектронавiдбуватисьсп ичинеíèй отонами, |
|
|
|||||||||||||||||
|
оловною ар ументацi¹ю для збереж |
|
ðîçâ'ÿçêiâ iç âiä'¹ì |
|
|||||||||||||||
|
åíåð iÿìè ¹ |
|
|
äè |
моренняДiрака |
стани позидо |
|
||||||||||||
|
|
енер iями. У класичнiй механ цi, де енер iя набува¹ |
|
|
|
||||||||||||||
еперервних значень,квантовiперехакi |
äè |
çi ñòð |
бками ¹ неможливи |
|
|||||||||||||||
. Квантовий перехiд |
|
|
дi акiвського моря станiв iз |
||||||||||||||||
âiä'¹ìíîþ åíåð i¹þ ìîæ |
|
|
ðiçí |
ìè øëÿõ |
. Напрлише |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
- |
|
|
|
|
|
|
|
|
|
|
|
|
âорю¹ати,зберенерiаналiзупередбаякженнярiга¹тьсзв'язанийякий,i¨.првиглядiЦемиякчивенерпроцесвибрало,iiстзвоакеан,i¨ная |
|||||||
|
|
|
|
|
ецьикненняелвимага¹,слектронно.електронноогозауважимо,позитронi¹мтiлачастиноквiдповiдно.--позитроннаПерш- що.Пiзнiжхоча.видiленнямАдо.параанiгiлюМдляпаризакону.анiгiляцi¨,Дiракутцього.Спост |
|
|
|
|
|
|
||||||||
|
|
|
|
å |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
електрон,процес,отони,називаютьтр |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|||||
|
Насамкi |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
застосовнапромiнювякийдваiмпульсумийротнийнародженнядночасне |
|
|
|
|
|
|
|
|
|
|
|
ÿêùî |
|
||||||
енер iя бiльша, нiж ширинапозитронно¨заборонено¨ зони 2mc |
|
|
|||||||||||||||||
ëè |
|
|
|
|
|
але зрозумiло, що ця iнтерпретацiя теорi¨ Дiрака |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
вирiшивнесподiванiпевною.й.ловилиПрокДiрак,мiроюнуврибурiо¨- |
|||||
|
|
|
|
|
|
|
|
|
|
|
âiëüíî¨о¹су¹тьснувавнiчрибалокмолодбурярелятивiстськ |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
рибалок |
|
|
|
|
|
|
||
чпроблемишення,àстинкизапропонованаНаПроВiдступостровiрозповiдаютьднiйП. .вiд'¹мних.Адо.Мвсiхвечiрок,.Дiрака,морi,задачачастинок,значеньцiкдеавуякийпро¨хякiйiстоспiненерзатрималарибалок:частобравiю,якихiйщодляучастьпропдорiвню¹на |
1/2 |
|
|
|
|
||||||||||||||
áó |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
øèñü ó àíöi (áóð âæ |
втихл ), |
äèí iç |
|
|
|
|
|
|
å |
ïî |
|
||||||||
äèòè ä óçi , |
|
взяти |
ñâîþ ÷ ñòêó ðèáè é íà ñâî¹ìó ÷îâí |
|
|
||||||||||||||
íà òðü õ, |
äí |
рибина ¹ |
|
. Âií ¨¨ âè |
|
, óçÿâ ñâîþ |
|
|
|||||||||||
ëþ |
поплив |
|
|
берег. Др гий |
балка, про |
|
øèñü |
íå çíàþ |
|
||||||||||
÷ , ùî |
éîãî |
|
|
вариш уж |
iдплив, |
|
èâñÿкинувтакомуроздiлитиж ан |
||||||||||||
плисти |
|
берег. Але вiн |
уважив, що, я що вилов |
|
|
|
|
||||||||||||
áèн спочатку? Дiрак моментзайвоюльно дав вiд |
âiäü, íå |
соромлячись |
|||||||||||||||||
третiм рибалкою iсторiя по |
торилась. Питанн : |
ñêiëüêè |
áóëî ðè- |
||||||||||||||||
â ùi: ùîá |
ðîçäiëèòè ðèáó |
íà òðü õ,îïèäíу довелось викинуст |
. Ç |
||||||||||||||||
¨¨ абсурдностi: було мiнус двi рибини. З |
погляду |
математики |
|||||||||||||||||
38* |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
595 |
|
це дна з можливих вiдповiдей. Загальний розв'язок цi¹¨ |
÷i ¹ |
|||
долю,булозалишилосьрибин, то пiсля того, як перший рибзада ка |
||||
забравпростимсвою.Якщо |
N |
2(N − 1)/3 пiсля другого зали- |
||
шилось |
|
|||
2[2(N − 1)/3 − 1]/3 |
= 2(2N − 5)розрах/9 |
пiсля третього |
||
2[2(2кратнимбалокN −. 5)Îòæå,öiëèì/9 −1]/3äâîõ,= 2(4Nîñêiëüêè−19)/27воно.Останн¹ число |
|
|||
|
|
овувалосьвиннао бутидвох |
||
ч сло. Остаточно2(4N −19)/27 = 2m, àáî 4N −19 = 27m, m öi å N = 5 + 7m −(1 + m)/4. Вiдповiдь дають чисëà mÀëå= âiäïîâiäü4k − 1, k =даютьвiдповiдь0, ±1, ±2, . . ., m = 3, N = 25; m = 7, N = 52, . . .
Моментальна |
яскравийm Äiðàê= −1, N = −2; m = −5, N = −29, . . .. |
||||||
космологi¨,нийванняП |
|
|
N = −2 |
|
- |
||
|
|
|
|
|
|
íiзикидартнихяселтронДiрака,(дивне.його.проблеми. )пiдх.магнiтсвбудiв¹ю |
|
|
|
|
|
|
енервеликихспiнорi¨,рiвнянастрималапозч |
|
|
|
|
|
|
теоретично¨ |
|
|
|
незрозумiлiстю.Азаряд.кореня.Дiракспiн,монопольквадрдовiд'¹мнiбàŸцетного74атьДiрак. знахСт а,ченняеричнийотриманнядазакприклад |
|
|
|||||
ìè |
Власнi |
|
моменту |
iëüê |
руху в заг льному |
êó |
|
|
â Ÿ33. Ó Ÿ35 |
кремо |
був розглянутий випадокäëÿ |
||||
спiнуквадратзнайшлиняпроекцi¨1/2, тобтоункцi¨моментуоли êвантовеiлькстi число,рухуостiвипадмаксщоèмальзначà¹е значенняласнезначенйого
îñòi |
|
|
|
|
|
|
- |
|
рухуj визна= 1/2ча¹тьс.Тямисумоюдослiдимоорбiтальногîк,iспiновогоколи м ммоментiв:кiль |
||||||
|
|
ˆ |
ˆ |
|
|
||
|
|
J = |
L + ˆs, |
|
|
||
Правила комутацi¨ |
ˆs = |
~ |
повногоσˆ . |
моменту |
|||
2 |
|||||||
тими самими, що й дляомутуютькпонент операторiв |
ˆ |
||||||
J ¹, очевидно, |
|||||||
операторiв |
|
|
|
|
ˆ |
части |
|
|
|
|
|
L |
ˆs. Компоненти |
||
|
ˆ |
ìiæ ñîá þ, îñêiëüêè äiþòü íà ðiçíi |
|||||
змiннi: операˆs îðàL ê |
|||||||
|
ˆ |
тiна. Зспiновiувагизмiннi,нацебудьLщовласних-предстяккомпонентавляютьна просторовi ¨¨к ператоратрiшнiдинати ступе ки,вiльноса ˆs |
|
вадратом |
ˆ |
J комуту¹ з його |
|
|
ˆ |
êцiй вiдповiдно2. Отже, вонизн чень:спiльну систему власних ун- |
|
|
J |
596 |
~2j(j + 1) à ~m. Êðiì òîãî, |
оператор ˆ2 |
комуту¹ з ˆ 2 i |
2. Справдi, |
|
|
|||||
|
J |
|
|
L |
ˆs |
|
|
|
|
ˆ2 |
ˆ |
2 |
2 |
ˆ |
ˆ 2 |
2 |
ˆ |
ˆ |
ˆ |
i îñêiëüêèJ = L |
|
+ ˆs |
+ 2 Lsˆ = |
L |
+ ˆs |
+ 2(Lxsˆx + Ly sˆy + Lz sˆz), |
|||
|
ˆ 2 комуту¹ сам зi собоюоператориомутузкомпонентами ˆ ˆ ˆ |
|||||||
бутиа ак ж з L |
|
|
|
|
ˆ |
|
Lx, Ly, Lz, |
|
¹ алярнийьсопера2 |
ò |
|
|
величини,2. Ò æ ñàìå ñòî- |
||||
|
ˆs |
îðàsˆx, sˆy, sˆz, òî âií ê |
¹ i ç |
J |
|
|
||
iñèññê |
емувимiрянимивласнихдобутоку2. Îòæå, |
ˆ2, |
ˆ |
2 |
2 |
|||
|
ˆs |
íочаснокцiйiпредставляють.азом з ними мож |
ˆs |
бутимаютьякiвимiрянимможутьспiльну |
||||
|
|
|
J |
L |
|
|
||
|
|
|
|
ˆ |
|
1 |
ˆ2 |
ˆ 2 |
|
|
2 |
|
|
|
|
як i добуток |
|
|
|
Lsˆ = |
2 |
(J |
− L |
− ˆs ), |
|
|
|||||
Власнi значення цих |
|
ˆ |
1 |
|
2 |
2 |
|
2 |
|
|
|
||||
|
èíˆâiäïîâiäíîˆ |
|
дорiвнюють |
||||||||||||
|
|
|
величJsˆ = |
2 (J |
|
− L |
+ ˆs |
). |
|
|
|
||||
òà |
~2 |
|
|
|
|
|
|
|
|
3 |
|
||||
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
j(j + 1) − l(l + 1) − |
|
|
|||||||||
|
2 |
|
4 |
||||||||||||
К антове число |
2 |
|
j(j + 1) − l(l + 1) + 4 |
. |
|||||||||||
|
~2 |
|
|
|
|
|
|
|
|
|
3 |
|
|
||
iâ ЗнайдемозŸ33,жтепернабуватиj, згiдно зтакiзагальнимзначення:правилом додавання момен тючихавласнiмiжзначення:собоюоперасис емуорiв.власнихПишемо ункцiйрiвнянняj = läëÿ± 1íà/âñiõ2власнi.цих омутуункцi¨-
ˆ2ψ = ~2j(j + 1)ψ,
J
Функцiя |
ˆ |
Jz ψ = ~mψ. |
ψ¹ дворядковою матрицею-стовпцем:
ψ = |
ψ1 |
. |
597 |
ψ2 |
Запишемо перше рiвняння в явнiй ормi, розкриваючи квадрат |
||||||||||||||||||||||||||||||
оператора ˆ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
J: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ˆ 2 |
|
2 |
|
|
ˆ |
|
2 |
j(j + 1)ψ. |
|
|
|
|||||||||||
Зважаючи на те,(ùîL |
|
+ ˆs |
+ 2 Lsˆ)ψ = ~ |
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ˆ |
2 òà 2, ìà¹ìî |
||||||
|
|
|
|
|
|
|
|
|
|
|
ψ ¹ власною ункцi¹ю L |
|
|
|
ˆs |
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
3 |
~2 + ~ Lˆ σˆ − ~2j(j + 1) ψ = 0, |
|
|
||||||||||||||||
причому |
~2l(l + 1) + |
|
|
|
|
|||||||||||||||||||||||||
4 |
|
|
||||||||||||||||||||||||||||
|
|
ψ1 |
òà |
ψ2 |
¹ с еричними ункцiями з орбiтальним кван- |
|||||||||||||||||||||||||
товим числом |
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
l. озпишемо матрицi: |
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
3 |
|
|
− |
|
|
|
|
0 |
1 |
|
|
|
ψ2 |
|
||||||
|
|
~2l(l + 1) + 4 ~2 |
|
~2j(j + 1) |
|
|
|
|
|
1 |
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
~Lˆx |
|
|
|
|
|
|
|
|
|
|
рiвнянь |
|
|
ψ1 òà ψ2: |
|
||||||||||||
|
|
+ |
0 1 |
+ ~Lˆy 0 |
|
− |
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
1 0 |
|
|
|
i |
|
0 |
|
|
|
|
|
|
|
|
||||||||
|
|
+ ~Lz |
|
1 |
|
0 |
|
|
|
ψ1 |
|
= 0. |
|
|
|
|
|
|
|
|
||||||||||
Звiдси знаходимоˆ |
систему двох |
|
|
|
äëÿ |
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
0 |
|
−1 |
ψ2 |
|
|
|
|
|
|
|
|
|
|
||||||||||
~2 l(l + 1) + |
3 |
|
− j(j + 1) ψ1 + ~(Lˆx − iLˆy )ψ2 + ~Lˆz ψ1 = 0, |
|||||||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||||
4 |
|
|||||||||||||||||||||||||||||
2 |
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
рiвняннi ˆ |
|
|
ˆ |
|
|
|
|
ˆ |
|
|
|||||
Якщо прийняти â |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
~ l(l + 1) + |
4 |
|
другому− j(j + 1) ψ2 |
+ ~(Lx + iLy )ψ1 − ~Lz ψ2 = 0. |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ψ1 = C1Yl,m i врахувати, що |
||||||||||
|
|
ˆзадоволенняˆ |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
òî äëÿ |
|
необхiдно взя и |
− m) Yl,m+1, |
|
|
|||||||||||||||||||||||||
|
éîãî(Lx |
+ iLy)Yl,m = |
~ |
|
(l + 1 + m)(l |
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p |
|
|
|
ψ2 = C2Yl,m+1 |
|
|
||||||||
му задовольня¹тьс |
i перше рiвняння тому, що |
|
|
|
|
. Ïðè öüî- |
||||||||||||||||||||||||
|
|
(Lˆx − iLˆy)Yl,m+1 = ~p |
|
Yl,m. |
|
|
||||||||||||||||||||||||
598 |
|
(l − m)(l + m + 1) |
|
|
||||||||||||||||||||||||||


знаходимо сталу нормування C1:
C |
|
dΩ ñY еричнi(θ, ϕ)Y óíêöi¨(θ, ϕ)+íî |
|
|
|
|
− |
|
Y |
|
|
|
(θ, ϕ)Y |
|
(θ, ϕ) =1. |
|||||||||
| |
2 |
l,m |
l,m |
|
|
|
|
l |
|
|
|
m |
l,m |
+1 |
|
|
|
|
l,m+1 |
|
||||
1|Z |
l+m+1 |
|
|
|
|
|||||||||||||||||||
Îñêiëüêè |
|
|
|
|
рмованi, òî çâiäñè |
|
|
|
||||||||||||||||
Îòæå, äëÿ |
|
C1 = r |
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
||||||||
|
l |
|
|
2l + 1 |
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
+ m + 1 |
|
|
|
|
|
|
|
|
|||||
|
|
j = l + 1/2 хвильова ункцiя |
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
||||
|
|
|
|
|
|
l+m+1 |
Yl,m(θ, ϕ) |
|
|
|
|
|||||||||||||
|
|
|
(j) |
|
|
2l+1 |
|
|
|
|
||||||||||||||
Аналогiчно для випадку |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
ψl,m |
= q l m |
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
q |
2−l+1 |
Yl,m+1(θ, ϕ) |
|
|
|
|
||||||||||||||
|
|
|
|
j = l − 1/2 ìà¹ìî |
|
|
|
|
|
|
||||||||||||||
Öiäëÿ |
|
ψl,m = |
q |
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|||||||
|
|
l+m+1 |
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
(j) |
|
l−m |
Yl,m(θ, ϕ) |
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
2l+1 |
|
|
|
|
|
|
|
|
|
|
|
рiвняннi Дiрака |
||||||||
|
Насчастинкиункцi¨цiкавитименазиваютьiззарядомнерелятиŸс75еричними. âiñòñüiвняннякийспiнорамиПаулiперехiд. |
|||||||||||||||||||||||
|
|
|
|
−q |
2l+1 |
Yl,m+1(θ, ϕ) |
|
|
|
|||||||||||||||
ëàìè |
|
|
|
e |
електромагнiтномó полi з потенцiа- |
||||
V |
A: |
|
|
|
|
|
|
|
|
|
|
|
|
|
ˆ |
|
|
||
|
|
|
|
HDψ = Eψ, |
|
|
|||
|
|
|
|
|
|
e |
2 |
|
|
Здiйснимо в цьомуˆ |
рiвняннi |
|
ормальний розкладˆ |
за степенями |
|||||
|
HD |
= αˆ , pˆ |
− c A c + eV + βmc . |
|
|||||
1/c. Запишемо його як систему двох матричних рiвнянь |
|||||||||
|
|
|
e |
|
|
|
2o ψ = Eψ. |
||
600 |
n αˆ , pˆ − |
|
A c + eV + βmcˆ |
||||||
c |
|||||||||

|
|
|
0 e |
|
|
|
|
σˆ , pˆ − c A c + eV I |
0 |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
e |
|
|
|
|
|
|
|
|
− c |
|
|
|
|
|
|
|
|
|
|||||||
|
σˆ |
, pˆ |
|
|
|
|
A c |
|
0 |
|
|
|
|
0 I |
|||||
|
|
|
|
|
|
|
|
||||||||||||
+ |
I |
|
0 |
mc |
ϕ |
= E |
ϕ |
|
|
||||||||||
|
|
− |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
або в явному виглядi |
2 |
|
|
|
|
|
|
|
|
||||||||||
|
0 |
|
I |
|
|
|
|
|
|
|
|
χ |
|
|
|
χ |
|
|
|
|
|
|
|
|
|
|
|
e |
|
|
|
|
|
|
|
|
|||
|
σˆ , pˆ − |
|
|
|
A cχ + eV ϕ + mc2ϕ = Eϕ, |
|
|
||||||||||||
|
c |
|
|
||||||||||||||||
Будемо розглядатиeрух власне елек |
2 |
à, êîëè |
|
|
|||||||||||||||
|
σˆ , pˆ |
− |
|
A cϕ + eV χ − mc χ = Eχ. |
|
|
|||||||||||||
|
c |
|
|
||||||||||||||||
íîþ ¹ óíêöiÿ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
E > 0 i ãîë â- |
||
в перше рiвнянняϕ. Мисистемивиключа¹моункцi¨позитроннi стани пiдстановкîþ
|
|
|
χ = |
|
|
|
1 |
|
− eV c |
σˆ |
, pˆ |
|
e |
|
||||||
|
|
|
E + mc2 |
− c A ϕ, |
||||||||||||||||
визначено¨ з другого |
рiвняння. |
Тепер для |
|
óíêöi¨ |
||||||||||||||||
рiвняння ма¹мо: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ϕ з першого |
|||||
|
|
e |
|
|
|
c2 |
− |
|
|
|
|
|
e |
|
|
2 |
||||
σˆ , pˆ |
− c A |
E + mc2 |
|
|
eV |
σˆ |
, pˆ |
− c A +eV |
||||||||||||
|
|
ϕ = (E − mc )ϕ. |
||||||||||||||||||
Вiдраховуючи åíåð iþ âiä åíåð i¨ ñïîêîþ |
|
|||||||||||||||||||
це рiвняння |
такому виглядi: |
|
|
|
E = mc2 + E′, запишемо |
|||||||||||||||
1 |
|
|
e |
|
|
|
|
− |
|
|
|
|
|
|
|
e |
|
|||
2m |
σìèˆ , pˆìà¹− c A |
1 + (E′ |
|
|
eV )/2mc2 |
σˆ |
, pˆ − c A +eV ϕ = E′ϕ. |
|||||||||||||
êÒолиепеð |
|
ìî çмогу перейти в ньомó äî íåðåëятивiстсько¨ межi, |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
äî |
Квазiрелятивiстське(Eнаближення′ eV )/2mcзнаменникуточнiстю1. |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
− |
|
|
|
|
|
|
|
||||
рiвняннi:мо, кщо знехту¹мо цим членом у |
|
|
|
|
першого1/cдоданкотримà¹â- |
|||||||||||||||
|
|
|
|
" |
|
σˆ , pˆ − ec A 2 |
+ eV # ϕ = E′ϕ. |
601 |
||||||||||||
|
|
|
|
|
|
2m |
|
|
|
|
||||||||||
