
Vakarchuk_I_O_Kvantova_mehanika_Pidruchnik_B
.pdf
ма¹девеличинаI iнтенсивнiсть падаючого на речовину свiтла в точцi z = 0,
0
2ω
змiст кое iцi¹нта поглинанняκ ñâiòëà′′ . Îòæå,
= c n
|
|
|
|
|
κ = |
|
4πωα′′ |
|
|
|
|
|
|
||
ма¹мо:або, пiдставляючи явний вигляд уявно¨n′c частини поляризованостi, |
|||||||||||||||
2π2e2N |
|
|
|
|
|
γ/2π |
|
|
γ/2π |
|
|||||
множиУрахувапiдсцейнняумовуваннявиразтемпературно¨на й овiрнiстьзалежностiреалiзацi¨ |
çïдiйснимо,очатковогоякщостанупо- |
||||||||||||||
κ = mcn′V |
k(k=n) fkn (ωkn − ω)2 + (γ/2)2 + (ωkn + ω)2 |
+ (γ/2)2 . |
|||||||||||||
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
X |
|
|
|
|
|
|
|
|
|
|
|
|
||
ïiäñóì ¹мо за iндексом |
|
|
|
|
|
|
|
|
|
|
ρn |
||||
ùîiндекси |
|
|
ïîìiíÿ¹ìîn. При цьомумiсцямивдругомуiурахуваннямдоданку того,нiмi |
||||||||||||
|
|
ωkn = −ωnk, |
|
fkn = −fnk, |
|
|
|
||||||||
остаточно знаходимо: |
ρk /ρn = e−~ωkn/T , |
|
|
|
|||||||||||
2π2e2N |
|
|
|
|
|
e−~ωkn/T )f |
|
|
γ/2π |
|
|
||||
Якщоспектκ = частотральнié |
ρ |
n |
(1 |
− |
|
|
|
|
. |
||||||
kn (ωkn |
− ω)2 + (γ/2)2 |
||||||||||||||
mcn′V |
n k(k=n) |
|
|
|
|
|
|
||||||||
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
X X |
|
|
|
|
|
|
|
|
|
|
|
|
|
¹â ëèøå äèí äîäàωлiблизькаíок,i¨: якийдо називре онà¹тьсянсно¨,коез iцi¹нтомусi¹¨суипоглинанняважливим
|
2π2e2N |
|
~ω/T |
|
γ/2π |
|
íюваннясок,доданок,як правспонякило,таннихй зменшунесутт¹вий,перехîдiвпогли |
унаслiдокзi збудженихня,ураховутого,а¹тьсстщовí |
iвесокатомiвуви |
||||
ЦейпромiДругийв κ = |
mcn′V |
ρn(1 − e− |
|
)fkn |
(ωkn − ω)2 + (γ/2)2 . |
|
542лемЯк бачимосп |
|
|
|
|
~ω/T 1 |
|
åктрально¨проi ьiнi¨коема¹iцi¹нтлоренцiвськийалинанняхарактерзбiг. Площаяз пропiдi-.

|
r |
|
|
|
|
||||
цимПрикладонтуром,лятора,рюванняченням, щоое. дозвСилаiцi¹нтосциляторабтоля¹ iнтепоглинання¨¨кспериментальнораллiнiйногоза ω12,.¹гармонiчногопропорцiйноювизначитиосциляторадочерезсили. Заосцивимiозна- |
|||||||||
а далi беремо з Ÿ22 вираз дляfknìàòð= |
2m |
2 |
|
||||||
~ ωkn|xkn| , оператора координати |
|||||||||
|
|
|
|
|
|
è÷íого елемента |
|||
|
|
|
|
|
|
√ |
|||
i пiдносимо його до квадðàòà: |
|
||||||||
|
~ |
|
|
|
|
|
|
|
|
xkn = |
|
2mω (√n δk,n−1 + |
|
n + 1 δk,n+1) |
|||||
| |2 ~
перехресний додан xê,knзрозу= ìiëî,[nδäà¹k,níóëü−1 +. (Ураховуючи,n + 1)δk,n+1] ,ùî
2mω
ωn−1,n = −ω, à
ωn+1,n = ω, ìà¹ìî îстаточно
Перевiримо правило сум:fknX= (n + 1)δk,n+1 − nδk,n−1.
а пiдсумовування за Xдругим iндексомfkn = (n äà¹+ 1) − n = 1,
k
невопормуякглинзпадiСистемаповинноанi,тисьннiприбути.заряджотона,Наприклад,.глинаннiякенихfkn Ÿ=ìà¹66(÷kàîòîíiâ−назвустинок,.ким1)Фотое+явищем1достатнь−оторозщеплення,якi(kåêò+ ïå1)¹ =ебувають−високо¨1, енераувириванняядерзв'язаноi¨ можепри-
n
до12иПослiдовкiнетичÿíèõогое виведеннярiвняннявиразудля отонiвдля оерозрахунокподаноiцi¹нтнацiов пiдручникпогсилинанняу: Iiверситет.шляхомО. Вакарчукпобу-. ТеорiяIвана Франка,зор 2002,спектрiвнаведено. Львiв: ж сциляторiв дляiменiво
äëÿ äîдiбнихслiдженняатомiв,структуриало¨ контурiвзагасЛьвiвськийàнняспектральнихγ, ое iцi¹нтальнийлiнiйрозсiяння,атома. необхiдних543
å |
л ктронiв |
|
атома пiд |
отона |
|
|
|
îòî |
|
|
|
ичним |
|||||||
|
àáî |
|
ñòî |
отое ектом. П оцесом, зворотним |
|
î |
|||||||||||||
й ектом,ного |
|
òîìà: |
при зiткненнi електрона |
|
|
ñèñò ìà ïå- |
|||||||||||||
рехнiзовдить у( отойонiзацi¨),збуджений стан iз наступн |
|
перехдода |
|
|
|||||||||||||||
ç |
випромiнюван |
ÿì |
тонiв у станиназиваютьусе нижчийономи |
значенняìè |
|||||||||||||||
òî åêòó |
|
|
|
|
|
|
äi¹þðàäiàöiéíà |
îìáiíàöiÿ |
åëåê |
|
|
òà |
|||||||
åíåð i¨ àæ äî |
'язанийос овного стану. |
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
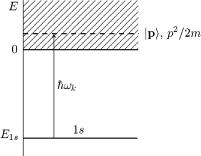
ис. 58. Квантовi переходи при тое ек i. |
|
|
|
|
|
|
||||||||||
|
озгляньмо задачу розрахунку |
|
|
|
îòîå åêòó. Íå |
|
|||||||||||||
|
E1s |
|
|
|
|
|
|
|
|
|
|
òåðìiâ |
|
|
K |
|
|||
хай електрон в атомi (див. рис. 58) ймовiрностiперебува¹ |1s |
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ценердою |
|||
оболонка),i¹ю |
(застанкласиелектромагнiтногоiкацi¹ю рент енiвськихполязад ¹ться-станiамплiтуз |
|
|
|
|||||||||||||||
|
|
|
|
óíêöiþ |
|
|
|
|
iвняннi |
|
|
|
|
|
|||||
|ç0åíåð, . . . , 0i¹þ, Nk,α |
= |
÷à¹, |
|
|
|
|
|
|
|
|
|
|
|||||||
1 0, . . . , як опису |
поляризацi¹юнаявнiстьдного отона |
||||||||||||||||||
чатковий стан,системихвильовиматомве торомплюсполе |
|
α |
àê, ùî ïî |
|
|||||||||||||||
|
|
~ωk |
|
|
k |
|
|
|
|
|
|
|
|
||||||
|
Кiнц вий'язаномуст| iñè= |1åìèsi|0, . . . , 0, Nk,α = 1, 0, . . . . |
|
|
|
|
|
|
|
|||||||||||
òðîí ó åç |
|
|
|
|
ñòàíiâçà¹ìî|fåíåði опису¹i¹ю |
вакуумний стан поля й елек |
|
||||||||||||
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
- |
|
|
овумалеУозназагальномуенезбуðення,iящоелектронавипадкуотонатобто¹шдiювеликмиидкiстьнуповиннiектронаоюовомуелектрона.поПричомубнаближеннiзатийономдлявважвважатимемизелектронаенерплà¹ìîзгляскоюi¹юве |
||||||||||||||||||
544йонiзацi¨ликоюхвилеюда¹мохвиль.як.Отже,.Це |
|
|
|
|
p |
|
/2m |
|
|
|
|
|
|
|
|
||||
точну хвильову ункцiю неперервного спектра. Таким чином: |
|||||||||||
|
|
|
|
|
|
|
|
|
кiнцевому |
|
|
де хвильова ункцiя електрона|f i = |pi|0,â. . . , 0, . . . , |
|
ñòàíi: |
|||||||||
E0 |
виразi |
|
|
|
àãнiтного |
|
|
||||
|
|
|
|
|
1 |
|
e pr/~. |
|
|
||
Випишiмо вiдповiднi енер|pi¨:= √ |
V |
|
|
||||||||
|
E(0) |
= |
E |
1s |
+ E + ~ω |
k |
, |
||||
|
|
|
|
|
|
0 |
|
||||
|
E(0) |
= |
|
p2 |
+ E0, |
|
|
||||
|
|
|
|
|
|
|
|
||||
|
f |
|
|
2m |
|
|
|
|
|||
|
|
|
|
|
|
|
|
||||
|
|
|
ймовiрностi поляквантового. переходу за |
||||||||
одиницюУ енерзагальномучасуiя вакууму електродля |
|
|
|
|
|
|
|
||||
доданок:в матричний елемент оператора вза¹модi¨ да¹ внесок лише перший |
|||||
|
2π |
|
(0) |
(0) |
|
wi→f = |
|
|hf |Vˆ |ii|2 |
δ Ef |
− Ei |
|
~ |
|||||
ˆ − e ˆ
оскiлькитмйвиписупоглинаннярозгрозрахляда¹моовували,резульсвiтладномеваннякладок, Vобчисат:=вотоннийŸ61.ëþþ÷è(Òîìó,Aперехiдp)iнтненси.поЦейâнiстьторюючиматрвипромiнючнийцихеле-
mc
Дельта- óíêöiÿ× |
δ |
2m |
− ~ωk − E1s . |
|
|
|||||||
|
|
2π |
|
e |
2 |
2πc2~ |
|
|
2 |
|||
w →f = |
|
~ |
|
mc |
|
V ωk |
hp|eikr(ek,αpˆ)|1si |
|
||||
|
|
|
|
p2 |
|
|
|
|
|
|
||
забезпå÷ó¹ виконання закону збереження енер i¨: |
||||||||||||
|
|
|
|
p2 |
|
|
|
|
|
|
||
35 I. О. Вакарчук |
|
|
|
|
− ~ωk − E1s = 0, |
|
545 |
|||||
|
|
|
2m |
|
||||||||

здеоберненимE це знаке ером,iя йонiзацi¨ атома, або робота виходу I, узята
1s
е екту, який установивE Айнштайн= −I. Отже,у1905ми отриму¹мороцi: закон ото-
1s
p2
вимиПiдсумуймоiмпульсамивиразелектрона,для~ωéìîâiùî= ðíâèëiîñ+òà¹iI.перехзатома:ду за всiма можли-
k 2m
X
нiвЯкщо( отонцювеличинунасодин)подiлитиw =на густинуw . падаючого потоку ото- |
|||||||||||
вання за |
|
|
|
|
|
|
jðiвняннi |
|
w вiд пiдсумову- |
||
|
|
|
|
|
|
|
p |
→f |
|
|
|
îòîå åêòó |
|
j = c/V , то ми отриму¹мо повний перерiз |
|||||||||
Перейдемо ста дартним чиномσ =ów . |
|
äëÿ |
|||||||||
|
p до iнте рування: |
|
|
|
|
|
|||||
|
|
|
äè åðåíöiàльний перерiз |
||||||||
Уведемо |
|
руваннσ = c (2π~)3 |
Z w →f dp. |
|
|||||||
|
|
|
V |
V |
|
|
|
|
|||
|
äëÿ iíòå |
|
ÿ |
с еричну систему координат: |
|||||||
Звiдси знаходимоσ = Z |
dΩ c (2π~)3 |
Z0 |
∞ p2w →f dp.îòîå åêòó: |
||||||||
|
|
|
|
V |
|
V |
|
|
|
|
|
|
|
dσ |
V |
V |
∞ |
2 |
|
|
|||
Нам залишилось îá÷ислити матричний елемент |
|||||||||||
|
|
dΩ |
= c (2π~)3 Z0 |
p wi→f |
dp. |
||||||
546 |
hp|eikr(ek,αpˆ)|1si = h1s|e−ikr(ek,αpˆ)|pi . |
||||||||||


ìà¹ìî: |
|
|
|
|
|
|
|
|
|
|
|
|
pka2 |
|
|
|
|
|
|
p |
2 |
|
|
|
|
2 |
|
||
1 + q2a2 |
= |
1 + a2 |
|
|
+ a2k2 − |
|
cos θ |
|||||||
~ |
|
~ |
||||||||||||
|
|
|
~ω |
|
|
|
~ω |
|
v |
|
|
|||
äå |
= |
|
|
1 + |
|
− |
|
cos θ , |
|
|||||
|
I |
2mc2 |
c |
|
||||||||||
¹ìîv нерелятивiстський= p/m швидкiстьвипадокотоелектрона. Оскiльки ми озгляда
ного перерiзу знаходимо: |
|
|
|
|
|
~ω mc2, то для ди еренцiаль- |
||||||||||||||||||||||||
|
|
|
dσ |
|
|
e2 |
|
|
|
|
|
|
(ek,αp)2 |
|
|
|
I |
|
4 |
|
||||||||||
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
||||||||||||||
Одиничний |
|
|
|
= 32 поляриçàöi¨a p |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
||||||||
|
|
(1 − vc cos θ)4 |
~ω |
|
||||||||||||||||||||||||||
|
|
|
dΩ |
|
mc ω~3 |
|
|
|
|
|||||||||||||||||||||
а хвильовий вектор |
|
|
|
|
|
|
ek,α спрямуймо взд вж осi x, |
|||||||||||||||||||||||
|
|
|
|
|
|
k уздовж осi z. У с еричних кîординатах |
||||||||||||||||||||||||
x-компонентазимутiмпульсу електрона |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
äå |
|
|
|
|
|
px = (ek αp) = p s n θ cos ϕ, |
|
|
|
|||||||||||||||||||||
ϕ |
|
|
альний кут. Остаточно |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
dσ |
|
e2 |
|
ap |
3 |
|
|
|
I |
|
|
|
5 |
sin2 |
θ cos2 |
ϕ |
|
|||||||||||
|
|
|
|
|
|
2 |
îò, онанайiìî( |
вiрнiш , що електрон вилiта¹ |
||||||||||||||||||||||
вОтже,напрямкуне |
ппарадоляриз= 64êàöсальнai¨ |
|
|
|
|
|
|
|
|
|
|
|
|
− |
|
|
|
|
|
. |
||||||||||
|
|
dΩ |
|
~c |
~ |
~ω |
|
1 |
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
vc cos θ |
4 |
|
||||||||||||||||||||||
п ширення тона ( |
|
|
|
|
|
|
θ = π/2, |
ϕ = 0). У напрямку |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
нцiальногозi отоелектроназбiльшеннямпеерiз |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
вперед |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
åð |
|
|
|
|
|
|
|
|
îгорiвню¹Привидкоствеликихймовнулевi.рнiсть.Знаменникенервильiяхквант)ó виразiелектронастьди вильоту |
|
|
|
|||||||||||||||||||||||||||
нийзбiльд |
|
|
|
|
|
θ = 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
√ |
|
|
|
|
|
|
||||||
перерiз |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
~ |
|
|
|
ди еренцiаль- |
|||||||||
|
|
|
dσ/dΩ (I/~ω)7/2. |
|
p |
|
|
2m ω |
ðîçñiÿííÿ (ïðè |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Повний перерiз |
|
|
|
||||||||||||
v/c 1) отрима¹мо iнте руванням за кутами: |
|
|
|
|||||||||||||||||||||||||||
|
256 |
|
e2 |
|
I |
|
5 |
|
|
~ω |
− 1 |
3/2 |
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
σ = |
|
|
πa2 |
|
|
|
|
|
|
|
, |
|
|
|
~ω ≥ I, |
|||||||||||||||
|
3 |
~c |
~ω |
I |
|
|
|
|
||||||||||||||||||||||
Повнийσ =перерiз0, îòîå~ω < Iåêòó. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
глинання548 |
електромагнiтного випромiнюванняσ да¹ змогу знайти.Алекцеое лишеiцi¹нтдинпо- |
|||||||||||||||||||||||||||||

iз механiзмiв поглинання. Пiд |
с проходж |
ня електромагн |
|
||||||||||||||||||||||
ãî |
ипромiню ання через речовину й |
î |
|
те си нiсть зменшу¹ть |
|||||||||||||||||||||
ÿ |
на лiдок процесiв як |
|
|
линання, |
òàê |
|
|
|
ëi |
ня. Iсну¹тноак |
|||||||||||||||
|
ñелективне поглинання, або |
|
ëèíàííÿ |
i¨, ÿê |
iäáó |
||||||||||||||||||||
âà¹òüñ |
|
íà |
ïåâíié |
частотi при перехпогдi мiж |
ди кретними рiвня и |
||||||||||||||||||||
званег ання. Поглинання |
|
íåïåðåðâному спектрi |
|
|
îìà |
||||||||||||||||||||
êâà |
òîâî¨ |
отое ектом, компто |
iâñ êèì |
ðîçñiÿ |
ням на вiлтрьних |
||||||||||||||||||||
|
|
|
(äèâ. |
ïîã |
|
днiй парагра ),iюваеперервне по |
|||||||||||||||||||
процесами:ëектронахсистемиу воренням електронно-позитрон их пар. Кое i |
|||||||||||||||||||||||||
|
|
ÿ iç ñóìè |
трьщох |
|
|
|
|
|
|
|
доданкiв, к жзумовленеяких дорiв |
||||||||||||||
да¹тьсв ницi об'¹му. Внесок у коезмiðíiц ¹нтiстьпоглинàíня отоелекòðè÷- |
|||||||||||||||||||||||||
|
поглинання, |
|
|
|
ì๠ð |
|
|
|
оберне о¨ довжини, скла |
||||||||||||||||
ю¹ добутковi е ективноговiдповiднихрер |
çó ïð öåñó |
êiëüêiñòü à îìiâ |
|||||||||||||||||||||||
мiститьцi¹нтогое ектудваелектрони,дляN атомiвдорiвню¹зурахуванням |
того, що K-оболонка |
||||||||||||||||||||||||
|
|
|
|
N |
|
512 |
|
|
|
e2 N |
~ω |
|
|
3/2 |
|
I |
5 |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
κ |
= |
|
|
2σ = |
|
|
|
πa2 |
|
|
|
|
I |
− 1 ~ω , |
~ω ≥ I, |
||||||||||
|
V |
|
|
3 |
~c V |
||||||||||||||||||||
Залежнiстьκ = 0, величини~ω < I. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
κ вiд частоти ω зображена на рис. 59. |
|
||||||||||||||
ис. 59. Залежнi |
|
ь кое iцi¹нта поглинан я електр |
агнiтного випро- |
||||||||||||||||||||||
|
. |
|
|
|
системи атомiв отоелектронокремомукiнцевому ст |
çíà |
|||||||||||||||||||
мiнювання вiд чаñòîòè. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
îâ íîìó |
||||||||||
õ ä |
|
|
розглянули явище отое екту на |
|
|
|
|
||||||||||||||||||
тьсДляв полi не лише вл сного |
йона, а вза¹модi¹iзольсiманi |
íàâ |
|||||||||||||||||||||||
атомiМик л шнiми атомами чи йонàми, i його хвильова |
óíêöiÿ, âiäïî- |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
549 |

вiдно до принципу суперпозицi¨, ¹ лiнiй ою комбiнацi¹ю плоских
хвиль,де центрованих найближчеоточуючих асти ках exp[ k(Rj − r)],
вiдютьсянийловнуRвза¹многоперерiзрольквадратомоординвiдiгра¹озсiяннярозтмодуляашуванняаj-огокоематричногоатомачастинок,iцi¹нтоточенняпоглинання,ченняелементщо.Отже,.отоЗрозумiло,а,уютьдизалежякiеренцiцейвизнатимутьщоатом:чальго-
j
κë æíîñexp[i îåk(Riöi¹íò− R )]поглинання.Цепричиню¹вiдчасосцилюючийоти характер за
j l
â |
|
|
|
нiчнихмиспекXвимiрючщоимiрюватиуватиå-нняrayрентда¹рiabsorptionатома,âскладнiмолекузмогуанняенiвсько¨рентпотенцiалзструктурвизначенiвськогоякогоструктури.Крiмneаstruвилiта¹нтиñEXAFSлинаннялишетдомзат-йонно¨îдиелектронпротвуEXAFSтвер-метоструктуру.ракцi¨яжноюЦейдихвза¹модi¨-сп.методозволя¹тiл,Нада¹ктроскопi¨тонкоецьомуа,найближчогозмiцi¹нтакразомоюккрема,гуонденсованихструктурунту¹тьсяiз(extended(рисжзшиметойпрямоорг.ото59),дароою |
|||
P |
електронтого,йтронно¨прометопогture)не |
ω = kc |
- |
|
- |
||
òiëàõ. |
|
|
поглинан я |
Приклад. EXAFS-спектроскопiя. Оцiнимо зсув к |
|
||
атомакраювiд iнцевогоκ, пзумовлелин няпотрiбнийзбуренням частинок середовищ , для частот, далеких
озрахоточеннiâó¹ìî |
|
|
ω I/~.íàì |
äëÿ |
обчислення |
κ матричний |
елемент |
||||||||||
ê kr у першомстзбурюючихану наближеннiелектрона,частинокякий. Заперебува¹теорi¹юминезбуреньпозналишеча¹мов(дивплiхвильову.Ÿ45),свогохвильоваатома,унк- |
|||||||||||||||||
ацiюунйв− |
(ek,αpˆ)|p), |
де круглими дужками |
|p) |
|
|
|
|
||||||||||
h1s|e |
öiÿ |
|
|
|
|
|
X |
|
|
|
|
|
|
||||
äå |
|
|
p) = p + |
|
hp′|W |pi |
p′ , |
|
|
|
||||||||
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
| |
|
|
| |
|
p′ |
p2/2m − p′2/2m |
| |
|
|
|
|||
|
|
|
|
|
|
|
|
|
(p′6=p) |
|
|
|
|
|
|
|
|
дi¨координатою|pi хвильова ун öiÿ електронадинаiзольованому атомi з номером a |
|||||||||||||||||
|
|
|
|
|
|
|
рона¹мо,(з оорщо екранованийòî÷êîþ ¹ |
плоск ми хви |
ÿìè; |
|
|||||||
енер iя вза¹модi¨,ами,елеквваж |
|
|
|pi |
′ |
|
|
|
W |
|||||||||
|
|
Ra |
|
|
|
елементинкашованими.Для |
|p i |
|
|
|
|||||||
|
|
|
|
|
|
äí |
сортно¨ псевдопотсистем |
|
|
||||||||
ма) з навколишнiми час |
|
|
|
|
|
|
r вiдносно èядраличинасвого ато |
||||||||||
P |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
W = |
|
електрона |
|
|
|
|
|
ак званий |
|
|
àõ |
|
åíöiàë âçà¹ì - |
||||||
j≥1 w(|r + Ra éî− Rj |) wðîçò |
|
|
|
|
|
|
|
|
|
||||||||
Отже, тричний |
|
|
|
|
|
|
|
Rj . |
|
|
|
|
|||||
|
|
|
h1s|e−ikr(ek,αpˆ)|p) = h1s|e−ikr(ek,αpˆ)|pi |
|
|
|
|||||||||||
550 |
|
|
+ |
|
X |
|
|
hp′|W |pi |
|
|
1s e−ikr (ek,αpˆ) p′ |
. |
|
|
|||
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
p′ p2/2m − p′2/2m h |
| |
| i |
|
|
|
||||||
(p′6=p)
Згiдно з означенням, кое iцi¹нт поглинання пропоцiйний квадратовi модуля |
||||||||||||
öü |
матричного елемент . |
цiкавлять |
еликi значення хвиль |
âåê |
||||||||
близькi |
|
|
p |
|
|
|
|
|
p′ |
p |
|
|
|
|
|
|
|
|
|
|
|
пiдсумовуванжна винести матричн й елемент |
|||
тораденогоk = ω/c, тому з-пiд знакНассуми за p′ |
|
ового |
|
|||||||||
1s e− |
kr |
(ek,αpˆ) p′ |
|
|
p′ = p |
|
|
|
|
|||
h | |
|
äî |
|
| |
i |
ïðè |
~k p′ |
цей матричний елемент (ek,αp′)/ω4 |
p′, |
|||
|
ливийтекс i, |
|
. Справд , к |
идно з його явногоправомiè ëÿäó, íà- |
||||||||
ог яду на те, що головний внесок при |
еквiвалдаватимуть векто .иА з |
|||||||||||
|
|
|
|
|
|
|
|
|
ля), тоналiззамiвнескуíàутово¨¹ залежðноюостi |
|||
величиниДопит |
|
Чит( наменникч,зробившиблизькийдетальнiшийдону |
|
|
|
|||||||
нання знах димоκ, i ó çâ'ÿçêó ç öèì äëÿ вiдносного зсуву кое iцi¹нта погли- |
||||||
|
(ek,αp′) |
|
|
|
|
|
iíòå |
ування ç кутамицей отрима¹моматричнийрезуелементат, ,змож |
п нтнийреконатись,замiнiщо пiсля |
||||
Тепер кое iцi¹нт поглинання: |
X |
|
p′ íà p. |
|||
|
|
|
|
|
2 |
|
äå |
κ |
|
κ0 1 + |
|
hp′|W |p |
, |
|
|
|
p′ |
p2/2m − p′2/2m |
||
|
|
|
|
(p′6=p) |
|
|
κ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
потрiбнокстi0 цьогокое парагрiц¹нт поглинаа. З урахуваняiзольованогонямтого,атома,щохвильовувиписанийункцiювосновно у |
|||||||||||||||||||||||||
взяли в першому нàближенíi çà åíер i¹ю збурення |
|
|
|
|
|p) ìè |
||||||||||||||||||||
|
брати i |
|
|
|
X |
|
|
|
|
|
|
W , ç òi¹þ æ î÷íiñòþ |
|||||||||||||
Матричний елементχ(p) = |
κ − κ0 |
= 2Re |
|
hp′|W |pi |
. |
|
|
||||||||||||||||||
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
κ0 |
|
|
|
p′ p2/2m − p′2/2m |
|
|
|
|||||||||||
|
|
|
|
XZ e−ip′r/~ |
|
|
|
(p′6=p) |
|
|
|
|
|
|
|
|
|
X |
|
||||||
′ |
|
|
|
|
|
|
|
|
|
|
e pr/~ |
|
|
wq |
q(Ra −Rj ) |
||||||||||
hp |W |p = |
|
√ |
|
|
w(|r + Ra − Rj |) |
√ |
|
|
dr = |
V |
|
e |
|
||||||||||||
|
V |
V |
|
|
|||||||||||||||||||||
|
Z |
|
|
j≥1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
j≥1 |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
wq = e−iqRw(R) dR, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
~iз номером′ |
|
iмпульс передачi. Узявши до уваги те, що видiлений атом |
|||||||||||||||||||||||
q = p |
− p |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a ¹забудь-яким з усi¹¨ сукупностi, цей матричний елемент можна, |
|||||||||||||||||||||||
пiдсумувавши |
a (a 6= j) i подiливши на кiлькiсть атомiв N , записати ак: |
||||||||||||||||||||||||
де структурний актор конденсованого′ |
òiëà |
− 1), |
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
hp |W |pi = wq (Sq |
|
|
|
|
|
|
|||||||||||
Тепер, |
|
|
|
|
Sq = |ρq |2, |
ρq |
= |
√1 |
|
XN |
e−iqRj . |
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
X |
|
N j=1 |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
χ(p) = 2Re |
1 |
|
|
wq (Sq − 1) |
|
. |
|
|
|
551 |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
V |
p′ |
p2/2m − p′2/2m |
|
|
|
|
|
|||||||||
(p′6=p)
