
Vakarchuk_I_O_Kvantova_mehanika_Pidruchnik_B
.pdf
деомуε наближеннiдiелектричнавекторпроникнiстьполяризацi¨. Для iзотропного тiла лiнiй-
íапруженостi поля |
P пропорцiйний до âектора |
|
E : |
величину |
P = αE , |
α називають поляризованiстю тiла. Отже, анiстюз теорi¨апокМàзниксвеллаом залома¹ìεоленн=çâ'1ÿ+çîê4πα,мiж дiелектричною проник-
ε = n2. Таким чином,
2
кальнерозрiдженихУзагалiполе,кажучи,системрезультатiцей.Длявиразгустихn÷îãî=визнача¹отриму¹мо1систем+ 4πα.показникнеобхiднодобревiдомийзаломленнявраховуватизв'язок:дляло-
личинаормула Клаузiуса |
n2 |
− |
1 |
= |
4π |
|
|
α |
|||
|
Мосоттi. |
Äëÿ àнiзотропного середовища ве |
|||
hd середн¹ значення дипоëüного моменту атома |
|||||
|
n2 |
+ 2 |
|
3 |
|
Äëÿ αрозрахунку¹тензоромполяризованостi.
ня, нам необхiдно знайти дипольний моментα, як виплива¹системиз ¨¨ означен- N àòîìiâ
|
наявностi |
N |
hdi, |
|
äå |
P = V |
|||
|
що Для спрощення ми озгляда¹моd = e rованого. дноеле тр нний атомтомуак,
|
r це радiу -вектор електрона, заряд яêîãî e = −|e|, |
|
||||
d = −|e|r. |
Якщо гамiльтонiан iзоль |
атома дорiвню¹ ˆ |
|
|||
поля гамiльтонiан |
Ha |
, |
||||
ïðè |
|
|
||||
äå |
|
ˆ |
ˆ |
ˆ |
|
|
|
H = Ha + V , |
|
||||
|
|
ˆ |
e |
|
|
|
532 |
|
V = − |
mc |
|
(Aˆp) |
|

оператор вза¹ |
дi¨ атома з полем. Ми нехту¹мо в |
|||||||||||||||
|
|
àòîì. |
пада¹ монохроматичне, як величиноюсвiтлочастотидругого по |
|||||||||||||
рядкуНехмайлизни |
|
|
|
|
|
|
|
|
2 |
|
|
|
операторi |
|||
вза¹модi¨ членом, пропорцiйним до A |
|
|
|
|
|
|||||||||||
|
|
отонiв,кажучи,им,iтобтотомумовавекторнийцьомуйдевипадкупротенцiалоперацi¨стан |
знищенняполяатимеправо.змiП |
|||||||||||||
|
|
çàäà |
|
|
|
|
|
|
|
|
|
|
|
|
|
ω |
I àêøå |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
пню¹тьслероджвважлядатиення.¹мо |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
мозгкл сич |
ою величиною. Чому i за яких умов ми ма¹мовваж |
|||||||||||||||
ð |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
- |
анiчногоотонiв якпогляду,класичнуцеознача¹,величину?що Покажмима¹ìî, макросщо,векторомопiчневанто |
||||||||||||||||
числоîòîíiâìåõ |
A |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
безмежностi,N частотою ω = ω |
k |
= kc, хвильовим |
||||||||||||||
|
|
k,α |
|
|
|
|
|
|
|
|
|
|
||||
k поляризацi¹юу цьому α.анМожна: го орити про сво¹рiдну |
онденсацiю |
|||||||||||||||
об'¹муознача¹,до що ¨хня густинаколи |
величиною. Макроскопiчнiстьсталоюпричислапрямуваннiото- |
|||||||||||||||
|
|
|
|
|
Nk,α ¹ 1 |
|
|
|
|
|
|
|||||
|
|
|
Nk,α |
|
|
|
|
|
|
|
|
V → ∞. операторiв пород- |
||||
женняУ цьомуiзнищеннявипадкудля |
V |
= const, |
|
|
|
|
|
|||||||||
|
|
|
отонiвсереднiхма¹мо:значень добуткiв |
|
||||||||||||
|
|
|
ˆ |
ˆ+ |
|
|
ˆ+ |
ˆ |
|
|
|
|
||||
або, враховуючи, щоhBk,αBk,αi − hBk,αBk,αi = 1, |
|
|||||||||||||||
|
|
|
|
|
|
ˆ+ |
ˆ |
|
|
|
|
|
|
|||
|
|
|
|
Nk,α = hBk,αBk,αi, отрима¹мо |
|
|||||||||||
|
|
|
|
ˆ |
ˆ+ |
|
|
|
|
|
|
|
|
Nk,α |
|
|
|
|
|
|
hBk,αBk,αi |
= |
1 |
|
+ |
|
|
||||||
|
|
|
|
|
V |
V |
|
|||||||||
i â ìåæi |
|
|
|
|
V |
|
|
|
|
|
|
|
||||
V → ∞ |
ˆ |
ˆ+ |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
Nk,α |
|
|
|
|
|
||||||
Це означа¹, що |
hBk,αBk,αi |
= |
= const. |
|
||||||||||||
|
|
|
||||||||||||||
|
|
|
|
|
V |
|
|
V |
|
|
|
|
|
|
||
такимсобою,чином,аотже,оператори¨хˆможнаˆ породженнярозгляˆ àòèˆ аякзнищеннякласичнiвисновкувеличини:омутують |
|||||
|
|
+ |
+ |
|
|
ìiæi, |
hBk,αBk,αi = hBk,αBk,αi |
|
|||
Bˆk,α p |
|
Bˆk+,α p |
|
. Ìè äоходимо |
|
Nk,α |
Nk,α |
, ùî ïðè533 |
|||
|
|
|
|
|
A = s V ωk |
|
|
|
ek,α nei |
залежностiBˆk,α + e− |
|
Bˆk,αo |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
поляго мовоюстану . Операторелек- |
|||||
векторноготромагмакроскопiчномуiтнепотенцiалуполезаповненнiможнадляописувативiдповiдно¨отонамикласичноюмодипев |
|
|
(k, α) |
|||||||||||||||||||||||
когозапису¹мозображурахуванняменняоператорiвчасово¨ |
|
|
|
|
|
|
|
|
|
|
вiд гайзенбер iвсь- |
|||||||||||||||
|
|
|
|
|
|
|
2πc2~ |
|
|
|
|
kr |
|
|
|
|
kr |
|
+ |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
e− Nk,αe |
|
(δ äåÿê |
початкова аза) |
|
p |
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Bˆk,α |
= |
eiδ |
|
Nk,α |
e−iωt, Bˆk+,α = |
||||||
|
iδ |
|
|
|
iωt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
як класичну величину: |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
A0 |
|
|
|
A |
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
A = |
|
|
|
|
e−iωt |
+ |
0 |
eiωt, |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
2 |
|
|
2 |
|
|
|
|
|
|
|||||||||||
хвилiМи розгляда¹моA0 = |
2e |
|
|
r |
|
|
ek,αe . |
|||||||||||||||||||
|
|
|
V ω |
|||||||||||||||||||||||
Таким чином,õâèëi |
Aвеличинуне |
|
|
|
òüñÿ, ÿêùî r çìiíþ¹òüñя в межах атома. |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
δ |
|
2πc2~Nk,α |
|
|
|
|
kr |
|
|
|||||
|
|
|
|
|
|
випадок дипольного наближення, коли довжина |
||||||||||||||||||||
зама.нестХвиль |
|
|
n |
|
|
|
|
|
|
àöiîíарного |
|
|
|
|
|
|
|
|||||||||
äå |
|
|
|
|
λ 1000 A, |
|
|
|
|
|
|
|
kr |
ka = 2πa/λ 1, |
||||||||||||
aТомудовжина порядку лiнiйних розмiрiв атома.
ïëiòóäà |
e kr 1 + · ·мiня¹·, о же,вваждовгохвильовому наближеннi ам- |
|||||||||||||||
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Нехай |
|
|
|
|
A0 |
à¹ì |
сталою. |
|||||||||
|
|
|
(0) |
(r, t) = e− ~ |
E |
(0)t |
ψ |
(0) |
(r) |
|||||||
¹ хвильовою ункцi¹юψ |
|
n |
|
n |
|
|||||||||||
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|||
ацiонарноюву ункцiютеорi¹юатома-гозбуреньствелектромагнiтному.Упершомустану iзольнаближеннiпîлiваногошука¹моато- |
||||||||||||||||
|
ψn(r, t) |
= |
ψ(0)(r, t) + |
X |
C |
(1) |
ψ(0)(r, t), |
|||||||||
|
|
|
|
n |
|
k(k6=n) |
|
|
kn |
|
k |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
(1) |
|
1 |
|
Z V˜kn(t)dt = |
1 |
|
Z |
|
Vkn(t)eiωknt dt, |
||||||
|
Ckn |
= |
|
|
|
|
|
|
||||||||
|
|
i~ |
i~ |
|
||||||||||||
534 |
ωkn |
= |
|
Ek(0) − En(0) |
, |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
~ |
|
|
|
|
|
|
|
|
|
|

а матричний елемент îïератора збурåííÿ
Будемо шукатиˆ |
|
|
|
|
e |
|
|
|
|
|
|
|
|
e |
|
|
|
|
|
|
|
|
|
|
e |
|
|
|
|
|||||||||
середн¹ значення дипольного моменту |
атома для |
|||||||||||||||||||||||||||||||||||||
Vkn(t) = hk|V |
|ni = |
−mc hk|Apˆ|ni = −mc Ahk|pˆ |
|ni = −mc Apkn. |
|||||||||||||||||||||||||||||||||||
очевид о, що i |
|
|
|
|
|
|
|
ëiíié |
доданок за |
(1) |
|
|
|
|
|
|
|
|
|
|
äî A |
2, òî |
||||||||||||||||
ÎñêiëüêèV |
не беремо |
|
|
|
|
|
до уваги член, |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
n-го квантового стану: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
hd = dnn = hn|d|n = Z ψn(r, t)erψn(r, t) dr |
|
|
|
i |
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
(0) |
|
|
|
|
|
|
|
|
(1) |
|
|
iωnk t |
|
|
|
(1) |
|
|
|
|
|
iωknt |
+ . . . |
||||||||||
Тут крапк=àìèdnn |
+ k(k=n) hCkn ernk e |
|
+ Ckn |
erkne |
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
позначено дода |
|
к, пропорцiйний доператоромквадрат |
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
C(1). |
|||
|
|
|
|
|
|
|
|
|
X |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
ð ííÿ |
|
|
|
працю¹моквадратичний íîму наближеннi за |
|
|
|
|
|
|
çîâíiø |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
çáókn - |
|||||||||||||||||||||||||||
ˆ |
|
|
|
|
|
|
|
|
|
|
ньому |
|
|
|
|
|
|
|
|
|
пропорцiйний |
|
|
|
, ÿê |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ckn |
у виразi для hd |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(0) |
|
|
|
|
||
н¹ значенняудругогодипольногопорядкумоìализни,ентунезбуреногонадалi атомаврахову¹мо. Серед |
||||||||||||||||||||||||||||||||||||||
величинтеорi¨ою еi дляектухвильШтарка,вих дорiвню¹ункцiйпевно¨левi,парностi,dяк ми¹сталоюбачи |
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
nn |
|
|
|
|
||
ми цiкавимосьполем.Такимлишечином,дипольним моме |
|
|
|
|
|
|
(0) |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
- |
|||||||||||||||||||||
том, iндукованимКрiм того, |
||||||||||||||||||||||||||||||||||||||
íiì |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dnn |
= 0. |
|
|
|
|
|
|
||||||
шогоде черезчленак.. .Далidnn |
= |
|
X hernk Ckn e |
|
|
|
+ . . |
|
, |
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(1) iωnk t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
позначеназнаходимовеличина, комплекснос спряжена до пер- |
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
k(k6=n) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
äîðiâíþ¹ |
|
|
|
|
|
|
|
|
|
|
ií |
òå |
|
|
|
|
|
(позна |
|
|
|
|
|
|
ëåì), |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
− |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
Ckn |
= i~ |
|
|
|
|
Z e ωknt |
|
02 kn |
) |
e−iωt |
+ |
|
(A |
02 kn |
eiωt dt |
|||||||||||||||||||||||
|
−mc |
|
|
|||||||||||||||||||||||||||||||||||
(1) |
|
|
1 |
|
|
|
e |
|
|
|
|
|
|
|
|
|
(A p |
|
|
|
|
|
p |
|
|
|
|
|
|
|
||||||||
1 |
|
|
|
|
e |
|
|
|
(A0pkn) |
|
eiωknt−iωt |
|
|
A0pkn) eiωknt+iωt |
|
+ 0. |
||||||||||||||||||||||
внесокМи = ~ |
|
|
−mc |
|
|
|
2 |
|
|
|
(ωkn |
|
ω) + |
|
2 |
|
|
|
|
i(ωkn + ω) |
||||||||||||||||||
тутвiдопунижньо¨сталумежiñòèëè |
|
|
|
рування |
|
|
|
|
÷åíó |
|
ó |
|
|
|
|
тобто |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t0 |
, уважаючи, що збуренíÿ ïðè |
t |
= t0 |
|||||||||||||||||||||
|
|
|
нулевi. Можна скористатись i так званою адiабатичною535 |
|||||||||||||||||||||||||||||||||||
гiпотезою, згiдно з якою вмикання збурення вiдбува¹ться посту-
значенняпово: вiд нулявмоментвдалекомучасу минулому, t0 = −∞, до його скiнченного t. Тепер
|
|
|
|
e2 |
X |
rnk |
(A p |
|
|
) |
|
|
|
|
1 |
|
|
|
|
|
||||||||||||||||||||
dnn = |
|
|
|
|
|
|
|
|
|
|
|
|
0 kn |
|
e−iωt |
|
|
|
|
|
|
|
||||||||||||||||||
|
mc~ k(k=n) |
|
|
|
|
2 |
|
|
ωkn − ω |
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
+ |
|
|
|
(A02 kn) eiωt ωkn1+ ω + ê.ñ. |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
p |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Переоада¹мо,= ~mc k(k=n) |
2 |
|
|
|
|
|
|
|
ωkn − ω |
+ |
|
ωkn + ω |
+ . . . |
|||||||||||||||||||||||||||
|
|
|
|
e2 |
X |
|
e−iωt |
|
|
rnk |
(A0pkn) |
|
rnk (A0pkn |
) |
||||||||||||||||||||||||||
ïишемооляçàìiцейсть вираамплзiтудчерèåçâекторногоамплiтудупотенцiалунапруженостi електричс - |
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
íàã |
|
|
|
ùî |
|
|
|
|
|
= −c −iω |
|
|
|
|
|
|
|
|
|
|
|
|
|
A0. Для цього |
||||||||||||||||
Îòæå, |
|
|
|
E = −c A˙ |
|
20 e−iωt |
+ iω |
|
20 eiωt . |
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
1 |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
A |
|
|
A |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
E 0 |
|
|
|
|
|
|
|
|
E |
|
|
|
|
|
|
|
||||||
де амплiтуда напруженостiE = |
|
|
e−iωt |
+ |
0 |
eiωt, |
|
|
|
|
|
|||||||||||||||||||||||||||||
2 |
2 |
|
|
|
|
|
||||||||||||||||||||||||||||||||||
Êðiì òîãî, |
|
|
|
|
|
|
E 0 = |
iωA0 |
, |
|
|
A0 = E 0 |
c |
. |
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
c |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
iω |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
pkn = mr˙ kn = imωknrkn |
|
|
|
|
|
||||||||||||||||||||||||
З уваги на це, |
|
|
|
|
|
|
|
|
|
|
|
|
rkn = rnk . |
|
|
|
|
|
|
|
||||||||||||||||||||
|
e2 |
X |
|
|
e−iωt ωkn |
rnk |
(E 0r ) |
|
|
|
(E 0rnk) |
+ ê.ñ. . |
||||||||||||||||||||||||||||
536dnn = |
|
|
|
|
|
|
|
|
|
kn |
|
− rkn |
|
|||||||||||||||||||||||||||
~ k(k=n) |
|
2 |
|
|
|
ω |
ωkn − ω |
ωkn + ω |
||||||||||||||||||||||||||||||||
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|

рiвностiозпишемозобразимотепер веяктïîîðäâî¹íóè çà êîìïäiéîñíåíòó ÷àмистину:i пðàâó ÷àстину цi¹¨
µ |
|
|
iωt |
|
e2 |
X |
ωkn |
|
|
|
xnkµ xknν |
xknµ xnkν |
ν |
|
||||||||||||||||||
dnn = Re e− |
|
|
X |
|
~ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 , |
||||||||||
причому iндекси |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
ν, µ = (x, y, z) |
|
|
ωkn − ω − |
|
|
|
|
|
||||||||||||||||||||||||
Уведемо |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
ν |
|
|
k(k=n) ω |
|
ωkn + ω E |
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
означення тензора. атомно¨ поляризованостi |
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
= Re ( |
|
|
βµν e−iωtE0ν ) . |
|
|
|
βµν : |
|
|||||||||||||||||
Отже, виходить, щоdnnµ |
ν |
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
X |
|
|
|
|
|
|
|
ïîëяризоваíîñòi, βµν |
||||||||||
|
|
|
|
|
e2 |
|
|
|
|
ωkn |
|
|
xnkµ xknν |
|||||||||||||||||||
|
|
|
|
|
X |
|
|
|
|
xknµ |
xnkν |
|
|
|
|
|||||||||||||||||
|
βµν = |
|
|
|
|
|
|
|
|
|
|
|
|
|
− |
|
|
|
|
|
|
|||||||||||
|
~ |
k(k=n) |
|
|
ω |
ωkn − ω |
ωkn + ω |
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
N |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
напрямленiозглянемополяризованостiвздовжнайпростiшийголовнихсистемосейвипадок,тензораè: |
ê |
|
ê |
|
ординатнi |
îñi |
||||||||||||||||||||||||||
а тензор |
|
|
|
|
|
|
|
|
αµν |
= V |
βµν . |
|
|
|
|
|
|
|
|
|
||||||||||||
δµν : |
|
|
|
|
X |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
e2 |
|
|
|
ωkn |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
1 |
|
|
|
|
||||||||
àáî |
βxx = |
|
|
|
|
|
|xnk |2 |
|
|
|
|
− ωkn + ω , |
|
|
||||||||||||||||||
~ k(k=n) ω |
|
|
ωkn − ω |
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Якщо в цьому виразiβxx = 2 |
e2 |
|
|
X |
|
|
ωkn|xnk|2 |
. |
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
~ k(k=n) ωkn2 − ω2 |
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
íà |
|
|
|
|
|
x |
çàìiíèòè íà |
y |
, отрима¹мо |
|
осцилятора,замiна : |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
βyy |
|
x |
||||||
z ä๠βzz . Уведемо величину, яку називають сила |
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
fkn = |
2mωkn |
|xkn|2. |
|
|
|
|
|
|
|
|
537 |
||||||||||||||
|
|
|
|
|
|
|
|
~ |
|
|
|
|
|
|
|
|
|
|
||||||||||||||
Òîäi
|
e2 |
|
fkn |
|
|
розгляд,iзотропноголяризованiрозрiдженñòîгоь ¹серескаляромдовища, з якого ми починали |
|||
нашДля |
βxx = m k(k=n) |
ωkn2 − |
ω2 . |
|
|
|
6 |
|
|
|
|
X |
|
|
ми отриму¹мо для показник заломлення10β: = βxx = βyy = βzz , i |
|||
2 |
4πe2N |
|
fkn |
залЦей млення,виразповнiстюпричомуn =âiäïîâiäà¹1âå+ ичинукласичнié îðìó.лi для п казника |
|||
|
mV |
k(k=n) |
ωkn2 − ω2 |
|
|
6 |
|
|
|
X |
|
лятора, якзалежноколивама¹змiсть кiëькостi оптичтежихназиваютьелектронiвсилiзîвласноюосци- |
|||||||||||||
частотою |
|
|
|
|
|
fkn |
|
|
|
||||
|
|
|
|
|
|
цю. Квантова.Дослiдмехпоканiкзувадатним,да¹днак,простещопоцеясненнячисло |
|||||||
цьому¹ меншим.Величиниди |
ωkn |
|
|
|
|
|
|
|
|||||
|
|
|
|
вонивiдможутьузнакквантовiйчабутитотиякдорiвню¹перех |
|
|
|||||||
числами,крiм того, |
|
fkn |
|
|
|
àнiцi вжду не ¹акцiлимивiд'¹мнимичила- |
|||||||
|
|
|
|
|
|
|
|
|
|
|
èницi.Легк.Справдi, |
||
ùî ¨õíÿ ñóìà |
|
першим iндекñîì |
|
ωkn |
|
довести, |
|||||||
|
fkn = |
|
2m |
ωkn|xkn|2 = |
|
|
|
m |
(ωknxknxnk − ωnkxnkxkn) |
||||
|
|
|
|
|
|
|
|||||||
k |
|
~ |
k |
~ |
|||||||||
|
|
k |
|
|
|
|
|
|
|||||
X |
|
|
X |
|
|
X |
|
|
|
|
|||
|
|
1 |
|
|
|
|
1 |
|
|
|
|
|
|
òóò = |
|
|
(xnk pkn − pnkxkn = |
|
hn|xpˆ − pxˆ |ni = hn|n |
= 1, |
|||||||
k |
~ |
i~ |
|||||||||||
|
X |
|
|
|
|
|
|
|
|
|
|
|
|
(теоремаОтже,¹ -Ткми |
|
айхлиеоператораакКуна):зване правиiмпуëьсуосумелектронадлясил. |
|
||||||||||
pˆ |
x омасаотримпонентою |
|
|
|
|
|
осциляторiв |
||||||
|
äiâà¹ìîñü, |
|
|
|
|
|
|
|
|||||
|
|
X |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
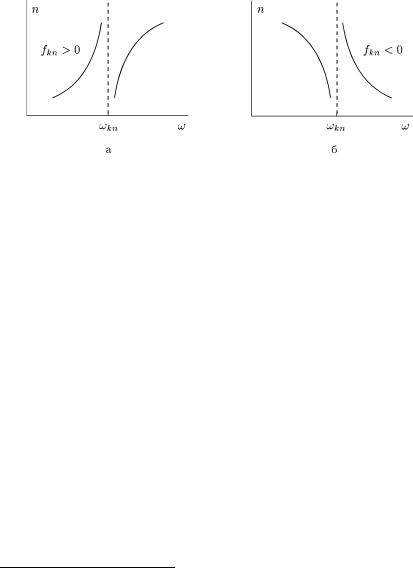
л нняНа рисдiлянцi.57 зображенарезонанснихчастотнаf =залежнiсть1äëÿ. додатно¨показника залом |
||||
|
|
|
kn |
|
|
|
|
k |
|
ïåðñi¨ ò âiä'¹ìíî¨ |
|
|
|
(fkn > 0) äèñ- |
чатков10Спого стану значкомщо(÷èòf |
ч<не0)буде, колиплутатитомнумерацiюзнаходитьсзаломленняхвильово¨в збудженомуункцi¨ по |
|||
|
kn |
|
|
|
|
|
|
|
|
538 |
n iз позначенням показник |
лiтерою n. |
||
ñòàíi: |
(0) |
(0) |
|
|
|
очевидноE âñi< En . Якщо атом перебува¹ в основному станi, то |
|||||
|
k |
fkn > 0. |
|
|
|
|
|
|
|
|
|
ис. 57. Поведiнка показник |
заломлення в |
резонансних частот: |
|||
а додатна дисперсiя; б вiд'¹мна дисперсiëÿíöi. |
|
||||
Цiкаво, що коли атоми середовища моделювати гармонiчними |
|||||
осциляторамиза частот ю |
ω0 |
анiвик заломлення пi ля пiд- |
|||
сумовування |
iндексом |
|
|
||
|
|
|
кiнцевих, то оказст |
|
|
вигляду (без явища вiд'¹мно¨ дисперсi¨)11: k набира¹ класичного
2 |
4πe2N |
|
1 |
|
|
рiвноваж |
|||
номуКолистанiсистемапритемператуатомiвn = 1çíà+iходитьймовiрнñÿ òåðiстьмодинамiчно. |
|||||||||
|
mV |
ω02 − ω2 |
|
|
|||||
в початковому станi з енеð i¹þT , òî |
|
|
|
перебування атома |
|||||
ìàíà |
|
En(0) |
зада¹ться розподiлом Больц- |
||||||
де статистична сума |
ρn = |
e−En(0) /T |
, |
|
|
|
|||
|
|
|
|
||||||
|
|
|
Z |
|
|
|
|
|
|
|
|
|
|
En(0)/T |
|
|
539 |
||
|
|
прикладi до цього парагра а. |
|||||||
11Сили осцилятора розрахованоZ = â |
e− |
|
|
|
. |
|
|
||
X
n
Запольногоозначенням,моментутермодинамiчне середн¹ iндукованого полем ди-
|
|
hdi = |
X |
|
|
|
|
||
Для поляризованостi |
|
ρndnn. |
|
|
|
||||
|
|
|
|
|
n |
|
|
|
|
|
|
α тепер знаходимо: |
|
|
|
||||
|
|
N e2 |
X |
|
X |
fkn |
|
. |
|
заломленняЗвiдсиВокможналi.резонанснотриматиα = èõ òчастотρn |
|
|
|
||||||
|
|
емпературну залежнiсть для показника |
|||||||
|
|
V m |
n |
|
k(k=n) |
ωkn2 |
− |
ω2 |
|
|
|
|
|
|
6 |
|
|
|
|
ми,Цевавши, |
|
|
|
|
ω = ωkn |
|
|
|
|
|
|
|
ацiонарнихââ атокзнаменникустмианмлiiâрозгрезонансн,узбудженихляда¹мо¹станiвлишееротримуанiквазiст¨атомнiч¹мовирази,стоти,анацiонарнинулiцiонарнiх,станимиурах.якПримубаяк-. |
||||||
|
огопрацюють,зробитиго.нема¹дополяга¹щобувагистацiонарнихпрацюватизамiноючасоскiлькитому,життястщо |
|
|
|
|
|
|||
|
ùî |
|
|
|
|
|
|
|
|
÷èимотацiонарнiмо,Длялегквзятицьсаме:не |
|
|
|
|
|
|
|
|
|
ñ |
|
|
|
|
|
|
|
|
|
íà |
|
|
|
|
ψn(0)(r, t) = e− |
i |
En(0)tψn(r) |
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
~ |
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
(0) |
|
|
E |
(0)t |
γn t |
ψ |
|
|
|
|
|
|
|
i |
(E |
(0) |
− |
i~γ |
n |
/2)t |
ψ (r), |
|
|||||||||
ò äëÿψспряжених(r, t) = e− ~ |
|
|
n |
− |
|
2 |
|
n |
(r) = e− ~ |
n |
|
|
|
||||||||||||||||||||
|
|
n |
|
óíêöié |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
íà |
|
|
|
|
|
ψ(0) (r, t) = e |
i |
Ek(0)tψ (r) |
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
~ |
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
|||
äå |
|
ψ(0) (r, t) = e |
i |
Ek(0)t− |
γk |
tψ (r) = e |
i |
(Ek(0)+i~γk |
/2)tψ |
(r), |
|
||||||||||||||||||||||
|
~ |
2 |
~ |
|
|||||||||||||||||||||||||||||
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
k |
|
|
|
|
|
|
k |
|
|
|||||||||
ваностiзуль знах |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
атомно¨ми таполяризо. У ре- |
||||||||
γk |
|
γn |
повторившисталiдимозагасанняпопереднiдля викладки,станiвзiндляекс |
|
k |
n |
|
||||||||||||||||||||||||||
|
àòi, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
540 |
|
e2 |
|
ωkn |
|
|
|
2 |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
1 |
|
||||||
βxx = |
~ k(k=n) |
|
|xkn| |
|
|
|
− |
|
, |
||||||||||||||||||||||||
ω |
ωkn − ω − i(γ/2) |
ωkn + ω + i(γ/2) |
|||||||||||||||||||||||||||||||
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
X |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|

äå γЗрозумiло,= γ + γ .ùî |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
k |
n |
|
|
|
|
|
|
|
|
|
|
|
íàìè: |
|
β i α в цьому випадку ¹ комплексними величи- |
|||||||||||||
α = α′ + iα′′, |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
e2N |
X |
|
|
|
|
|
ωkn |
ω |
|
ωkn + ω |
|
||
α′ |
= |
|
k(k=n) fkn |
− |
|
− |
|
, |
|||||||
2mωV |
(ωkn − ω)2 + (γ/2)2 |
(ωkn + ω)2 + (γ/2)2 |
|||||||||||||
|
|
|
|
6 |
|
(ωkn |
|
|
|
|
|
. |
|||
α′′ |
= |
πe2N |
X |
|
γ/2π |
|
γ/2π |
||||||||
2mωV |
k(k=n) fkn |
− ω)2 |
+ (γ/2)2 |
+ |
(ωkn + ω)2 + (γ/2)2 |
||||||||||
Êîìïлексним ¹ i показник заломлення |
|
|
|
|
|||||||||||
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
= |
n′ + in′′, |
|
наприклад, |
|
|
|
|
|
|
|
|
|
|
n2 |
= 1 + 4π(α′ |
|
|
||||
|
|
|
|
|
|
|
|
+ iα′′) |
|
||||||
|
|
|
|
(n′)2 − (n′′)2 |
= 1 + 4πα′, |
|
|
|
|||||||
|
|
|
|
|
резонансно¨ |
2πα′′ |
|
|
|
||||||
Як бачимо, в околi |
|
|
|
n′′ |
= |
часто.ти величини |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
n′ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
- |
нiстьтуватиимиКомзменшу¹тьсяй.ïУлексоказмiруíèпрохйхз.àЯкщорактерломлення,джпропорцiйнасвiтлопоказниксвiтламаютьпоширю¹тьсчерезскiнчзаломленняннiчовинуя, легкченняйого i.íòåуздовжрпренсив,аз |
|||||||||||||||
îñi |
|
|
|
|
|
|
|
|
споненцiальíî |
|
α′ òà α′′ |
|
|||
|
z, òî àìïëiòóäà õâèëi |
|
|
z: |
|||||||||||
|
|
|
|
äî |
|
|
|
|
|||||||
äå |
|
|
|
eikz = e ωv z = e ωc zn = ei ωc zn′e− ωc zn′′, |
|
||||||||||
æíà |
|
õâèëi,iö ¹íò ïîãøèренання ñâiòëà длявсередовищiсередовища.Звiдсичерез |
|||||||||||||
|
v = знайтиc/n iнтенсивнiстьшвидкое |
|
|
|
|
|
|
|
|||||||
n′′ |
|
|
мплiтудивдi, |
|
|
ексвiтла I, яка пропорцiйнаспада¹зiзбiльшенням |
|
||||||||
ìî.дуляСпр |
|
|
|
|
|
|
|
|
|
|
|
квадрата |
|||
|
|
|
|
|
|
|
|
|
I = I0e−κz , |
|
541 |
||||
