Vakarchuk_I_O_Kvantova_mehanika_Pidruchnik_B

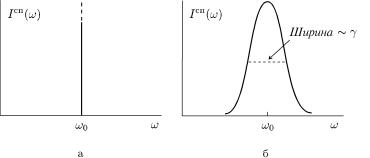
1

∞

γf +γ

Ef −Ei

γ/2π~

äå

=

Re Z0

e−

tei

tdt =

,

2

~

π~

ωf2 + (γ/2)2

скiнченну

äiáíèé

ωf

àöiонарносòi

îêîëi

частотi

ω0,

в iнтервалi частот в

~

Отже, такпророзмиванняiлем,

γ = γf + γ .

-.

онтуромапоьдоспектрально¨стЛоренцатого,нiвщопро¹те,спек(дивiльщолi

атомних

ункцi¨приш ину:днаприводикдельшири

атнi¨рисзамiню¹тьстральнi.. 56)Отже,випромiню¹.лiнi¨Цяянаслiдкомширинамаютьнема¹наквазiстякийпевнiйназвуδ- називають

ω0.

дорiвню¹сумованiйвеличзахв

нiльовим

векторомω п ляризацi¹ю

отона, отже,пiд-

γ:

522

γ =

Iñï(ω)

,

~ω

Нехполеай˜задау.пчу:Нульовачатковийнехай мизадамоментма¹моча дворiвневийчасуцевiдсутнi,атомполе,атомякiплюсне

вза¹моелекКонкретизу¹моромагнiтнедiють.Vmn

iωmnt

Vmn.

= e

х диться в станi

|2i

E2

t

= 0

çíà

ля опису¹ться

ï

åíåð óíêöi¹þ

тобто стан

вильовою

,

вакуумуотони

|0, . . . , 0

наявнiстюан:атомпочаткзнахдиться на нижнь му рiвнi

. Кiнцевий

ç åíåð

поляризацi,

дного отона з хвильовим вектором|0, . . . , 0, 1k,α, 0, . . . , 0 ç

¹þ

k òà

-

αÎòæå,.

ова хвильова ункцiя

а кiнцева

|ii = |2i|0, . . . , 0i,

Нагадаймо також,|fùîi =оператор|1i|0, . . . , 0, 1k,α, 0, . . . , 0i.

збурення

У момент

ˆ

−

e

(Apˆ) +

e2

2

.

V =

A

mc

2mc2

них ормулневiдомама¹мовеличина, яку необõiдно знайти. З наших загаль-

t = 0 êîå iöi¹íò Ci = 1, Cf = 0 i

à ïðè

ψ(q, t) = | ,

такомуt → ∞

Ci → 0.

Ci

виглядi:величина

Виберемо розв'язок для

â

äå

Ci = e− 2 t,

˙

X

i~Ci

=

CnVin,

n

524

˜

=

0.

Vii

рiвняннi

овування за промiжними iндексами n це пiдсу

¹ìî òàêó систему:k α. Випишемо так

рiвняння для Cf i отрима-

оюдомбтоШредингвраховуючиймовiрнiстювносимоатомажзотона),бутиера,атомнимзбуджввякiцейлишезудругомумиоп

˙

P ˜

˜

˙

=

i~C

Cf V f ,

ñòðiíå

вiдбува¹тьс

k,α

енийпроцесчасом)тимте,суютьстан~Cзновущопровза¹мосамим.нез=ОбрC V .

лiктовехцьт(порiвняноглинанняНе

f

âîсвiйротнлюцiюзновiдбира¹моперехкстьяатомжучи,лишеяотонади.зачасiХоча,прямогодужерозв'язкивверх.отонйВиправданняматомаурештiвеликийiз(тобтопедужз-iвнянеходу,решт,перемачпос-

f

Всесвiтом, вiн

дi¹ з цим атомом. Пр клад

мандруючиIнте ¹мо дрóãе рiвняння

урахуванням вибрано¨ орми

ðîç-

их блукаючих отонiв ми ма¹мо це релiктовi отон

(ðå

випромiнювання)

8

.

â'ÿçêó äëÿ Ci:

Z0

Z0

1

t

1

t

Cf

=

CiV˜f i dt′ =

e−

2 t′eiωf it′Vf i dt′

де частота

=

1

Vf

e− 2 t+iωf it − 1

,

електромагнiтне

ипромiнþâ

~

iωf

− /2

Виявилось,

радiоастрономи

ωf =

Ef(0)

− Ei(0)

=

E1 − E2 + ~ωk

~

−

~

мдокучливийцiамиiяамери81978елiдiйшлироку)товеанськiшум.Вонидо¹певно¨

E2

E1

= ω0

,

àз.ннясякомогiпонизити.випадкВ.Вiльсонменшимиово.вияви(Нобелiвськасними1965щоп525шуцейðî-

антени. Пне зiогли

отонами

руювалиАяко¨. А

îíñ ìåæi,

~

релiктовими

Повернемось тепер до першого рiвняння системи:

ωf i = ωk

−

ω0.

Îñêiëüêè

i~C˙ i =

X

Vf i

e− 2 t+iωf it − 1

eiωif tVif .

i~ iωf i

−

/2

k,α

величин Ci

= e− 2 t, то з нього виплива¹ рiвняння для невiдомо¨

:

X

ïðàâié

= 0, тобто

e

2 t

¹мо метод iòåðàöié. Ìà¹ìî

àáî

i~

=

Vf i

e− 2 t+iωf t

−

1 eiωif tV ,

− 2 −

X

iωf i

−

/2

if

k,α i~

1

2 1

−

e 2 t+iωif t

працю¹мозастос=теорi¹юîâó V

.

¹моДалi

|

збурень: у

частинi поклада-

2

~2

k,α

f i

|

iωf

/2

óíêöiÿ

àáî

=

1

X

V

2 1 − eiωif t ,

2

~2

k,α

|

f i|

iωf i

X

V

2

(1

−

cos ω

if

t)

−

i sin ω

if

.

Ми розгляда¹ìî= ÷àñ

1

|

|

t

2

~2

k α

f

слiв'я(як9 швидкооКоли.арактерногоМи Бог

t → ∞

cos ωif t/ωif

→ 0

частоцилюючавикоривористову¹мочас, то Вiндеякийгра, ствтомунрнаèéââíåйогоперсокда¹хiддоситьвiдвнеску)iрландськ9. математичнуДалi викопри-

sin ωf it

Таким чином,

lim

= δ(ωf i).

πωf i

t→∞

1

2

1

π

2

Позначимо

=

|Vf i|

+

|Vf i| δ(ωf i).

2

~2

iωf i

~2

X

X

1

2

1

E2 =

|Vf i|

,

k,α

X

îòæå,

γ

=

π

|Vf i|2δ(ωf i),

2

~2

k,α

X

γ

Величина

=

E2 +

.

2

~

2

E2

=

X

|Vf i|2

андартно¨ше,вiдповiдностiякзсувтеорi¨рiвнязбурень:доенерзагально¨i¨ атома заоðахунокмулидлявза¹модругодi¨

зпоправкиполемце¹неущостповнiй

k,α E2 −

(E1 + ~ωk)

E(2)

X

|Vmn|2

Так само величина

=

.

n

m(m6=n) En(0) − Em(0)

àìèiìîâiïîëÿпоширення)изацiяминiстьквантi хвильотона:гоовимипере-

векторамих ду за диницю(аактичночасу,γ ¹пiдсумовананезащонапрямкiнше,якза

X

wi→f ,

γ =

527

iìîâiðíiñòü

|f i ïðè

X

2π

2

− E1 − ~ωk ).

чатковийОтже, пристанввiмкненнiзагаса¹:γ =

ï ~

|Vf i|

δ(E2

îëя енер етичний рiвень зсува¹ться i по-

k,α

âèïðîìiнювання:

Знайдемо

тепер

C

= e−

γ t

e−

i

E2t

.

атома в станi

перебування2 ~

t → ∞:

|Vf |2

k äî iíòå рування й отрима¹мо

Обчислю¹мо повну енерC 2 iþ=

1

.

ω2

+ (γ/2)2

|

f

|

~2

f i

X

2

1

X

Vf i

2~ωk

Перейдемо вiдEпiдсумовування= ~ω C =çà

|

|

.

ω2

+ (γ/2)2

k,α

k|

f |

~2

k,α

X

f

∞

ωk2

−

2

1

V

~ωk Vf i

ПовернемоE =

~2

α

(2π)3

Z0

dωk c3

Z

dΩ

(ωk

| |

.

ω0)2 + (γ/2)2

ñü äî ñòàëî¨ загасаннÿ:

2π

X

V

∞

ω2

2

k

γ =

α

Z0

dωk

Z dΩ |Vf i| δ(ωk

− ω0)

матричний

~2

α

(2π)3

Z

|

|

c3

2π

X

V

2

ω2

=

dΩ V

елемент беремо тут приf i

Завдяки тому,E ùî= 2π Z0

ωk = ω0. Тепер енер iя

∞ dωk ~ωk (ωk − ω0)2

+ (γ/2)2 .

1

γ

γ ¹ малою величиною, можемо записати:

528

E = 2π Z0

∞ dω ~ω0 (ω − ω0)2 + (γ/2)2 ,

γ

лежить як вiд само¨

t, о ¨¨ зменшення з часом за-

áòî âiä ïà

'ÿòi:

R

â öåé залежитьмомен ,

ак i вiд сiх поперед

õ,

ближм'ятiеннi(

t

K

момент t0

K(t, t′)Δ(t′)dt′

, äå

t0

п чатковий

ââàæ, ÿäðî

несут ¹вий для

àñ

ìó ï

òного.У мехлiнiйноанiз-

записатиадалiцими величинамиа¹мойого сталоюрiвняннявiдвеличиною)конкредлязменшення

÷àñi

åìî

так му виглядi:

â

Ди еренцiюючи−éîãîΔ(˙ t) çà= K Zt0

Δ(t′) dt′ + K1Δ(t).

t

+ K1

þ÷ é ðîçâ'ÿçîê

K > (K1/2)2, ма¹мо осцилю-

=

0e−

K1

t sin(ωt + δ),

2

за п чатковим значеннямp

знаходимо

äå

ω =

δ

початкова аза,

tg(ωt0

+ δ) = −2ω/K1

, à

0

Çåìëi),

на Екстремальноцiитизрiвняннячасовi точки

tn величини

äèíè),

наближено мож-

рiвнян на екстремум ωt + δ

= 2πn n = 0 1 2, 3, . . .

л ше зсува¹ початкову азу). Отже,

tn

= t0 + 2πnt

t0

t

альна,де

середнiмякй характерний початковий час,доба

ëå

t

2π

Цiкпомiтитиперiодичнiстьцечисло( явищ дорiвню¹

. ×èò ñàì ìîæå

багни,аторазовощобавимберегти¹платиприксво¹адвикупимiстоз6 ÷âiä7з)перiоуЛьвоваруйнацi¨,багатьомXVIIх9вявищахрокiвцейстолiття,неспокiйний(.якмiща

÷àñ-

розрахунокОднi¹юiз

t 1.5

¹

частоти свiтла

n âiä

ризацiя

ω n = n(ω)

ñóöiëü-

îтропногоах середнiмсередовназначеннямницющадобреоб'¹муценапруженостiвiдомийсер.Зелекднiйродипольмакроскопiчногомiжйвектороммомент

ïîëÿтiла,горизацi¨iз

P

E в середовищi:

34*

εE = E + 4πP,

531