
Vakarchuk_I_O_Kvantova_mehanika_Pidruchnik_B
.pdfКутоваПерех |
залежнiсть |
|
|
|
|
|
|
|
|
|
|
випромiнювання ¹ склад |
||||||||||||||||||||
демо правил вiдбо |
|
. Ïî÷ iìî |
4 |
|
ìàãíiòíèõ äèïî |
|||||||||||||||||||||||||||
îþ. Ìè íå áó |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|||||
|
|
|
|
аналiзувати цi¹¨ залежностi |
|
|
|
|
|
|
||||||||||||||||||||||
полiльних |
|
|
|
|
|
|
|
|
квадрупольногоцентральновздовж -осiсиметричному. Матрич- |
|||||||||||||||||||||||
ний елементперехдимонадiвхвильових.Спрямуймоункцiяхопеатор µˆ |
|
|
|
|
|
|
|
|
z |
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
µz |
= n′, l′, m′ µˆ |
n, l, m |
i |
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
12 |
|
|
|
|
h |
|
|
| |
z | |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
= µBhn′, l′, m′|Lˆz |n, l, mi |
|
|
|
|
|
|
|
||||||||||||||||
Îòæå, öi |
перехбезвипромiнювальнiдийдутьбез змiни ква тових |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
= µB~mδm′,mδl′,lδn′,n. чисел |
|
|
|
|
|||||||||||||||||||||
àê çâàíi |
|
|
|
|
|
|
|
|
|
|
|
|
переходи. Для |
|
|
|
|
n, l, m öå |
||||||||||||||
мо змiни магнiтного квантового числа íà |
|
|
|
µx |
|
òà µy |
|
матиме- |
||||||||||||||||||||||||
|
диницю,12 |
12 |
|
|
||||||||||||||||||||||||||||
Äiéñíî, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m′ |
= m ± 1. |
|||
µx |
|
= n′, l′, m′ µˆ |
|
n, l, m |
i |
= µ |
|
n′, l′, m′ |
Lˆ |
n, l, m |
i |
|||||||||||||||||||||
|
12 |
|
h |
|
|
|
| |
|
|
x| |
|
|
|
Bh |
|
|
|
|
|
| |
|
x| |
|
|
|
|||||||
|
|
|
= |
|
1 |
µ |
n′ |
, l′, m′ |
Lˆ+ + Lˆ− n, l, m |
i |
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
2 |
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
Bh |
|
|
|
| |
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
~ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
= |
µBδn′,nδl′,l nδm′,m+1pl(l + 1) − m(m + 1) |
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
2 |
|
|
|||||||||||||||||||||||||||
Аналогiчно + δm′,m−1p |
|
|
|
|
o . |
|
|
|
|
|
|
|
|
|||||||||||||||||||
l(l + 1) − m(m − 1) |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
~ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
µ12y |
= |
µBδn′,nδl′,l nδm′,m+1pl(l + 1) − m(m + 1) |
||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||
|
2i |
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
тут iз Ÿ33 вирази для матричних елементiв опе- |
||||||||||||||||||||||||||
раторiвМи використали− δm′,m−1pl(l + 1) − m(m − |
1)o . |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
Спосiбнаведеноiнте. руванняПрикладiзакутами1довеличин,цьогопараграскладениха. iз декiлькох скалярних |
||||||||||||||||||||||||||||||||
512добуткiв,4 |
Lˆ |
± |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
У порiвняннiТепер займемосьелектричними дипольнимиквадрупольнимиперех дамиперехода¨хня йìи. на кiльк порядкiв менша, тому що ¨х породжують у
вiрнiстьаршiдляpкiльки членивидимрозк¨дiвеличелектричнимиянкиаду спектраспоненти за величиною kr ka. Îñ
12
шенняого iнтенсивностейзапорядком квадрупольногостановитьвипромiнювання−3,квадрутовiднодип
ka = 2πa/λ 10
ëüíiçтриватибудженийаабороненi,спектральнаатомйогоосновнийзнахлiнiячасдитьсправилаж¹знаяттячнозиваютьстцьомуслабшоюнi,зякогост−çàíi6. бiльними¹Отже,дипольнурахунокзнач мперехзiткненьПерехiд.Якщомоïîæäè-
10
мiжцихДлячазнайденiчиненихмiнюванняðà ñòинктутза¹мостан5−iâ2розраху¹моами,правиласекнадi¹ювлення.колиТакiтiлькивiдборустанматричнийможзелектромагнвiдбуватисьсвiдборуормульованiелемент,метаст¹ квадрупольногоншиминаприклад,здлятнимà .перехЗазначимо,ем.дiв,.оператвипросщо-
10
Qxy: |
|
|
|
|
|
|
|
|
|
|
h1|Qxy |2i = 3ehn′, l′, m′|xy|n, l, mi |
|
|
|
|
||||||
= |
3ehn′, l′, m′|r sin θ cos ϕ r sin θ sin ϕ|n, l, mi |
|||||||||
|
3eR Z0 |
2π |
|
|
|
|
dϕ |
|||
= |
e−im′ϕ cos ϕ sin ϕ eimϕ |
|||||||||
|
|
|||||||||
2π |
||||||||||
|
π |
|
|
|
|
|
|
|
|
|
де радiальний iнте× |
Z0 |
|
2 |
θ Θl,m(θ) sin θ dθ, |
||||||
Θl′,m′(θ) sin |
||||||||||
|
ðàë |
|
|
|
|
|
|
|
|
|
|
(1889 1974), |
|
Rn,l(r)r |
|
dr |
|
|
|||
роксьне33 5ийдорiвню¹ахПравилаI. Оученийзавiдував. ВакарчуквiдборуВнулевi. каубiновичедроюRдляпри= Z0 |
Rn′,l′ r)r |
|
|
|
|
|||||
|
|
∞ |
2 |
|
2 |
|
|
|
||
|
|
|
|
|
|
|
|
- |
||
|
|
|
|
|
åнняхЛьвiвськодiв установиавквантоуогоЛьвовióíièõâерситетуiдомийвчисел1937поль..1941513Iн |
|||||
|
квадрупольнихтеоретично¨будь-якихякийзначiзикиперпрацю |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
òå ðàë çа азимутальним кутом обчиñëю¹мо елементарно: |
|
|||||||
|
|
2π |
|
|
|
âiäì |
|
|
|
1 |
|
im′ϕ |
imϕ dϕ |
1 |
(δm′,m+2 − δm′,m−2). |
|
|
|
2 |
Z0íàøe−матричнийsin 2ϕ e еле2π = |
4 |
|
||||
âè, Îòæå,ùî |
|
|
ìåíò |
|
альногоий вiд нудля за умо |
|||
ëà |
òî ìèm′використа¹мо= m 2. Щорекурентнiдозмiниорбiтспiввiд ошенняквантовогоункцiйчис |
|||||||
|
|
|
|
± |
|
|
|
- |
Θ |
Äëÿ= Θвипадку(θ) з попереднь го парагра а. |
|
||||||
l,m |
l,m |
|
m′ = m − 2 ìà¹ìî |
|
|
|
||
|
|
|
|
|
|
|
||
sin2 θ Θl,m(θ) = |
sin θ |
Al,m′ Θl−1,m−1 + Bl,m′ Θl+1,m−1 |
|
|||||
|
|
|
= |
Al,m′ |
Al′−1,m−1Θl−2,m−2 + Bl′−1,m−1Θl,m−2 |
|||
|
|
|
+ |
Bl,m′ |
Al′+1,m−1Θl,m−2 + Bl′+1,m−1Θl+2,m−2 |
|
||
|
|
|
= |
Al,m′ |
Al′−1,m−1Θl−2,m−2 + Al,m′ Bl′−1,m−1 |
|
||
Аналогiчно для+ Bl,m′ Al′ |
+1,m |
1 Θl,m |
|
2 |
+ B′ |
B′ |
Θl+2,m 2. |
||||
|
|
m′ = m + 2 − |
|
− |
|
|
l,m l+1,m−1 |
− |
|||
sin2 θ Θl′,m′(θ) = Al′′,m′Al′′−1,m′−1Θl′−2,m′−2 |
|
||||||||||
|
|
+ Al′′,m′Bl′′−1,m′−1 + Bl′′,m′Al′′+1,m′−1 Θl′,m′−2 |
|||||||||
Тепер iнте ру¹мо+у виразiB′ Bäëÿ′ |
матричΘ |
ого елемента. |
|
||||||||
|
|
|
l′,m′ l′+1,m′−1 |
l′+2,m′−2 |
|
||||||
òîì |
|
|
|
|
|
|
|
|
|
Qx,y çà êó- |
|
|
θ i врахову¹мо ортогональнiсть уíêöié Θl,m(θ): |
|
|||||||||
|
|
eR |
|
|
|
|
|
|
|
|
|
h1|Qxy |2i = |
3 |
δm′,m+2 Al′′,m′Al′′−1,m′−1δl,l′−2 |
|
||||||||
4i |
|
||||||||||
|
+ |
Al′′,m′Bl′′−1,m′−1 + Bl′′,m′Al′′+1,m′−1 δl,l′ |
|
||||||||
|
+ Bl′′,m′Bl′′+1,m′−1δl,l′+2 − δm′,m−2 |
Al,m′ Al′−1,m−1δl′,l−2 |
|||||||||
|
+ |
Al,m′ Bl′−1,m−1 + Bl,m′ Al′+1,m−1 |
δl′,l |
|
|||||||
514 |
+ |
Bl,m′ Bl′+1,m−1δl′,l+2 . |
|
|
|
|
|
|
|||

|
|
|
|
|
32n |
|
|
|
2 |
|
|
P |
|
|
|
|
|
|
|
|
4π |
|
|
3n |
|
||
Iз цього |
|
|
|
|
|
|
4XX |
|
|
||||
äå |
|
виходить ще низка цiкавих |
|
|
|
|
|
нехай A = i≥1 |
Ai, |
||||
Ai незалежнiZ 42Xвектори: |
|
|
|
|
|
|
|
|
|||||
Зокрема, |
|
|
(eAi)5 |
dΩ = |
|
|
|
(AiAj )5 . |
|
||||
|
i≥1 |
2n + 1 |
|
|
|||||||||
|
|
|
|
|
Z dΩ = 4π, |
i≥1 j≥1 |
|
|
|||||
|
|
|
n |
= |
0, |
|
|
|
|
|
|||
|
|
випромiнювання21 |
|
|
типольноñòi |
|
|
|
|
||||
ÿêà |
|
|
|
|
|
äi¹þ |
|
||||||
|
|
λ = 21 |
= |
випромiню¹тьс |
|
M 1 |
|
|
|
||||
Äëÿ |
|
|
n |
, |
(eAi)(eAj )dΩ = 4π |
(AiAj ). |
|
||||||
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
n = 2: |
Z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(eA )(eAj )(eAk )(eAl ) dΩ = 4π |
[(A Aj )(Ak Al) |
|
|||||||
|
|
|
|
|
|
|
|
|
15 |
|
|
|
|
ЦiивностiноюПрормулихв кладлi ¹2.корисними+Ëi(A Ak )(âèùî¨ïðèAj.AСпектральуl)ìó+реднен(A Al)(iàAçàëiíiÿj Aкутамиk )].атомарного. ля розрахункуводюдовжиiнтен
структуриелектронавiдповiда¹енерззамагнiтниметичногоцiсмрiвнi, спектра,моментомзумовлено¨ÿдрапри(протона)вза¹мо-перех.Частинамiжмагнiтамiльтонiана,вямиогомоментонко¨-
äå |
|
|
|
|
|
|
|
|
ˆ |
|
|
|
|
|
|
|
|
|
.ˆsДляp операториобчисленняспi |
|
|
|
|
H = Aˆseˆsp, |
отона,творимоA з алаповногообмiнно¨моментувза- |
||||||||||||
¹ìîäi¨ˆse |
|
електронаетичногораломспект |
||||||||||||||||
, |
|
|
|
åíåðiâ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ˆ |
|
+ ˆsp його квадрат, який ¹ iнте |
|
|
|
ðóõó: |
||||||||||||
J = ˆse |
|
|
|
|||||||||||||||
|
|
3~2/4 çíàõ äèìî |
|
|
2 |
|
операторiв |
|
||||||||||
|
|
|
|
|
|
ˆ2 |
|
|
|
|
|
2 |
|
|
|
|
||
Çâiäñè |
|
|
|
J |
= ˆse |
+ ˆsp + 2ˆseˆsp. |
|
|||||||||||
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
||
|
|
|
|
|
ˆseˆsp = |
|
|
|
ˆ2 |
− ˆse |
− ˆsp) |
|
||||||
гамiльтонi н |
|
2 |
(J |
|
||||||||||||||
Тепер |
|
|
поправка |
|
|
ˆ i¨ |
A |
|
ˆ |
2 |
|
2 |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
||||
|
|
|
|
|
|
H = |
2 |
(J |
|
− sˆe |
− sˆp). |
|||||||
|
|
ïåðøà |
|
äî åíåð |
|
(1) |
|
|
|
ˆ |
|
|
|
|
||||
дорiвнюютьзурахуванням того, |
ùî |
|
|
|
|
|
|
|
|
|
спiнiв електрона i протона |
|||||||
квадратиE = h H , |
|
|
||||||||||||||||
|
|
|
|
(1) |
|
|
A |
~ |
2 |
|
|
|
|
− |
3 |
|
||
516 |
|
|
|
Ej |
|
= |
|
|
|
j(j + 1) |
|
. |
||||||
|
|
|
|
2 |
|
|
2 |
|||||||||||
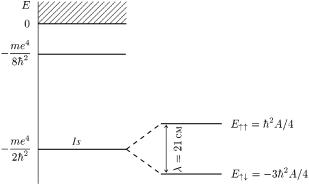
Квантове число j в цiй з дачi може набувати лише два значення (див. Ÿ33): jâiäíi= 0 значеннядля антипаралельненерi¨ ¹ кèхмиспiнiв(рис.i55):j = 1 для паралельних спiнiв. Вiдпо-
|
(1) |
|
3 |
2 |
|
(1) |
|
A |
2 |
|
Отже, рiзниця |
E↑↓ |
= − |
|
~ |
A, |
E↑↑ |
= |
|
~ |
. |
4 |
4 |
= E↑↑(1) − E↑↓(1) = A~2.
ис. 55. Надтонк |
ðîçù |
|
|
для основного стану атома водню. |
|
|||||
Експерименталь |
çíà÷åпленнявiдповiдно¨ ч стоти випромiнювання при |
|||||||||
|
|
|
|
|
|
|
радiоастрономi¨,ö |
|
|
|
розщепленнi рiвня енер i¨ для основного стану àтома водню (n = 1, l = 0, |
||||||||||
m = 0): |
|
|
|
|
|
|
|
|
|
|
довжина хвилi |
ν = |
/2π~ = 1420405751.800 ± 0.028 |
|
|
||||||
забороненими,Електричнi квадрупольнi |
|
åðåõλ äè21 (ñì. |
|
|
|
|
||||
повiдно¨тизамiнуймовiртомуостiцеперехмагнiтнеду |
0′ |
|
0 |
|
|
|||||
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
- |
|
|
|
|
|
|
|
|
|
ляомизровiд¹ |
|
|
|
|
ïридипврахуваннiîльне випромiнювання-перехспiну електронади)мiж.Уцимивиразiнеобхiдрiвí |
|
||||||
ˆ íà ˆ |
|
|
|
|
|
|
ЮендеакоскiлькиiюлстЕдвардж,ущоу1944ЛейденiсамеПарселзароцi517неюна. |
|||
Весноютодiцiйзначають6довжинiнiкомуЛiнiюЛiнiя19512121L |
L + 2ˆse. |
|
|
|
|
|
|
|
|
|
невiдомийрозподiлхрокусмсмилi¨¨вiдiгра¹упроводятьекспериментальнорадiоспектрiатомарногоголландськийважливупошукводнюалактикирольстудентiншихвиявилиВсесвiтiцивiлiзацiйвпершеендарольд.икЦiкавованпередбачив6. |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|

|
Ÿ 64. Час життя збудж |
|
станiв атомiв. Природна |
|
|||||||||||||||
|
|
|
|
|
ширина сп |
ктральних |
ëiíié |
|
|
|
|
|
|
|
|||||
|
лiнi¨ ¹ безмежно |
вузькимиiнтенсивностеймають |
|
дельтаподiбíий харак- |
|||||||||||||||
З айденi вир зи для |
|
|
|
|
|
|
|
|
|
íÿ |
|
ïî |
|||||||
глинання свiтла |
àтом ими системами говорять |
те, що спект |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ацiонарним |
||||
життелектромагнiтногорех¹ñòàíïóñêi¨êâàçiñòдить.штЧасдiвомвипромiню¹,али,я якiцьiзосновнийквазiстжперебуванняацiонарнимилишещозбуджмиперебувативважлосктрон,иховна¹моан,ацiатомнстанiватомайякбезмежнорухаючисьнарногостстанчерезó¨в атомно¨вiдповiда¹системистанизбудженомупевнийдовгоанузатомi,системинижчою...ПричичасIншиминайменшеНасправдi,статому.деякомуУсiоювузькимсловами,спонтанноспонтаннихзбуиваютьначенняi¹юстдженiспектральнiзв'язi,врчасомстанипереномуприштiнер- |
|||||||||||||||||||
ральнiер. Тобто атом випр мiню¹ацiонарнимипевнiй випромiнюваiксованiй частотi ω = |
|||||||||||||||||||
(E2 − E1)/~, що вiдповiда¹ квантовим перех дам мiж |
|
|
анами |1 |
||||||||||||||||
ò |2 |
âçà¹ìîäiÿ |
|
|
|
|
з нульовими |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
чиною спонтанних перех дiв ¹ |
|
дiя заряду |
полеоливаннямиiки,як вiн |
||||||||||||||||
|
|
|
|
|
|
оля. М вою класично¨ |
|
|
äèíà |
|
|
ïðè |
|||||||
ц онарнiсть збуджених станiв приводить доелектрого, що |
|
|
|
|
|
|
|||||||||||||
ÿê íå |
|
ïèò |
|
. Почнемовза¹мокласичного |
ро гляду. На ру |
||||||||||||||
ñàì |
iзольовано¨ |
|
|
ак звана реакцiя |
|
|
|
|
|
|
. Êâàçiñò - |
||||||||
|
атомно¨ сис еми не безмежнвипромiнювання |
|
, |
ìà |
|||||||||||||||
ëiíi¨. Мiжатомна вза¹модiяназивають |
òåïë âi ðóõè àòîìiâ ñïð ÷èíþþòü |
||||||||||||||||||
деяку ширину яку |
|
|
|
природною шириною спектрально¨ |
|||||||||||||||
Òåîðiÿ |
|
дно¨ ширини спектраль их лiнiй |
тонким i аж нi |
||||||||||||||||
подальше розширення спектральних лi iй. |
|
|
|
|
|
|
|
|
|||||||||||
знайтипростимямимщо |
аннямрт для |
використовуючи запiзнюючi п тå |
|||||||||||||||||
öiàëè |
|
|
|
|
|
|
|
поля точкового за- |
|||||||||||
хомий заряд, |
|
|
â |
ïðî |
iню¹, дi¹ сила Лоренца, створена ел к |
||||||||||||||
тромагнiтнимприро |
|
|
самого заряду. Вираз для |
öi¹¨ |
ñèëè |
|
|
||||||||||||
розрахуядучастинавипромi518США,eЛi¹нара.Вираз,юваннякипаратуризакiлькдеВiхякзгорiлабчисленням,триюлстйжнiвотриму¹момiсяцiа,.ПотратившипередАвстралi¨пiзнiшеелектромагнiтногопочаткдлязачамериксили,с наспостереженьоллан¨¨анцiввiщоäновлення,i¨.дi¹.У голландцiв,навиниклазаряд,вони прийняпожежякiмомажнаëèi

розкластиКвантовая втеорияядзаизлучстепåíияями. М1./c: ИЛ,(див1956):., наприклад, В. айтлер.
|
|
|
fL = − |
4 ε0 |
|
|
2 e2 |
|
|
|
||||||||||||
äå |
|
|
|
|
|
|
v˙ + |
|
|
|
|
|
v¨ + · · · , |
|
|
|||||||
|
|
3 |
c2 |
3 |
c3 |
v |
|
|||||||||||||||
ε0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
зазначити,кiсть,Запишемокрвл щопкснацеймиiвняннялектростнадрозкладлiрухуатичнаерами¹дляасимптотичнпозначенiзарядуенерiямасизаряду,похiднi. за часомйого.швидСлiд |
||||||||||||||||||||||
лу реакцi¨ випðомiнювання т |
|
çîâíiøíþ ñèëó m0, ураховуючи си- |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f : |
|
|
|
|
|
|
|
4 ε0 |
v˙ |
|
|
|
|
2 e2 |
|
|
|
||||||||
|
|
|
m0 + 3 |
|
= |
|
|
|
|
|
v¨ + f . |
|
|
|||||||||
|
|
|
c2 |
3 |
c3 |
|
|
|||||||||||||||
Множник бiля прискореннÿ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
безмежнiстю, |
|
|
|
4 ε0 |
|
|
|
||||||||||||
ì๠|
|
|
m = m + |
|
|
|
|
|
|
|
|
|
||||||||||
|
|
масильно¨ масипроязаряду0 ля¹тьс.Внутрiшнявтому,неузгоджщовеличи |
||||||||||||||||||||
|
змiсткласично¨спостережувчастинаелектродинамiки |
|
|
|
3 c2 |
|
|
|
||||||||||||||
îþ áåç åæí þ |
2 |
|
4ε0/3c2 для точкового заряду ¹ |
|||||||||||||||||||
|
|
|
|
|
|
|
|
r0 → 0. |
|
|
|
|||||||||||
тромагнi |
|
ε0 c /r0 |
|
|
|
|||||||||||||||||
iñòü ìпенсу¹тьсяногоданокспостерiгх дженнявиразi |
|
|
|
|
|
|
|
|
|
|
|
|
|
неелек- |
||||||||
|
(наприклад,якУважормуа¹ться, силамищоцябезмеж |
|||||||||||||||||||||
езультатi |
|
|
|
|
|
|
|
m0 |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
ìè |
а¹мо скiнченну велич силину Казимира),асаючiв |
|||||||||||||||||||
Другий до |
ó |
|
|
|
|
|
|
äëÿ |
|
fL |
|
m. |
|
|||||||||
нiшньо¨ухувипромiнюючогосили заряду. |
|
|
дитьквазiпружно¨догальмув зовння- |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
Наприклад,приводля |
|
|
||||||||||
коливання7 f = −mω02r розв'язок рiвняння руху да¹ заг |
||||||||||||||||||||||
з частотою |
|
r(t) = r0 cos(ωt + δ) e−γt/2 |
|
|
||||||||||||||||||
|
|
ω = ω0 − 5γ2/8ω0 i сталою загасання |
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
2 e2ω02 |
|
|
|
|||||||||
неУ резульматимеатiдельiнтенсивнiстьаподiбногопогγõ=араклинтераннóÿ. венероколii¨точцiчастотиакимосцилятором |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
3 mc3 |
|
|
|
|||||||||
ункцi¹ю частоти з гострим м симумом у |
|
|
ω0, à áóäå |
|||||||||||||||||||
7Див. вiдступ наприкiнцi цього п рагра а. |
|
ω0. |
519 |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
до квантов го опису. Шредин ера для
хвильчасi:Перейдемоово¨замiнаункцi¨ ψ(q, t) опису¹, як миiвнянянняз а¹мо, яви а зворо нi
спряж |
¨ хвильt наово¨(−t)ункцi¨приводить до рiв |
для к мплексно |
||||||||
рлiнiйзбукимзв'язки |
|
ψ (q, t) |
|
|
|
|
|
íамихв- |
||
|
|
|
|
|
|
|
|
|
атома. |
|
|
|
|
|
|
|
|
îòðiáíiектральвоно |
|||
|
|
|
|
|
|
|
ù |
|
|
|
|
|
|
|
|
|
|
ï |
|
|
|
|
джХвильчи. Однакíîì.овуПочнемостанi,цеспроможнеункцiюажливозтимпратомасамимстихпояснитизробити,еноменологiчнихприроднускiнченнийякщо. Здавалосьвiдбиратиширинучсби,мiркуваньжиттяс |
|
||||||||
iç |
|1 |
|
суперпозицi¨, |
|
системi, |
що склада¹ться |
||||
= ψ1 i збудженим |2 |
= ψ2. Ó |
|||||||||
ïîвною системою ункцiй, щоψопису¹= ψ(q,стацiонарнit) розклада¹мостани: яд за |
||||||||||
|
сукупностi N таких |
|
ìà¹ìî |
|
|
|
|
|
|
|
|
|
|
X |
|
|
|
|
|
|
|
|
|
ψ(q, t) = |
Cne− ~ Entψn(q) |
|
|
|
|
|||
|
|
|
Óíàñëiäîê |
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
ймовiрностi знах дженняатомiв,мадворiвневийстанi |
|
2 äîðiâíþ¹ |
||||||||
де, згiдно з принципом |
|
|
êîå iöi¹íò |Cn| |
|
|
|
||||
нимДля простоти розгляньм |
|
|
ψnатом. зi станами: основ- |
|||||||
записатиатомiвзбуузбудженомудженомутак:станiстанiзменшу¹ться.| |2зависвiчуваннязаконом,яêийiлькiстьприродноато-
N2 = N C2
|
|
îñòi |
dN2 |
|
|
де стала загасання γ = w2→1. Çâiäñè виплива¹, ùî |
|||||
äå |
w2→1 |
|
− dt |
= N2w2→1 |
, |
çi |
|
|
òанiомiвустанчасi. йзбуджено.да¹Тобто ìó ââñò íiæà¹ìïð -, |
||
|
збудженогiмîвiрнiстьану квантового переходу за одиницю часу атома |
||||
порцiйнащо Цешвидкiстьрiвняння¨хнiйзменшеннякiльквж|¹2незворотнимосновнийцьомучислаа |
|1i |
||||
N2 = N e−γt
i кое iцi¹нти розкладу залежать вiд часу: |
|
|
|C2|2 e−γt |
520 |
C2 e−γt/2. |

У загальному випадку врахування спонтанних перех дiв, коли
Ciân e−γnt/2, як бачимо, приводить до того, що стацiонарних ñòà-
íå iñíó¹, |
à ìà¹ìî |
|
ψn(q, t) = e− |
i E t |
ψn(q) |
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
квазiстацiонарнi |
~стани:n |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
ножник з |
|
|
|
ψn(q) = e− |
|
Ent− |
γn |
t, |
|
|
|
|
|
|
|
|||||||||||||||
|
~ |
2 |
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
γn |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Причому декрементда¹¨хзагЧасзагасання. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
вiрнiсть переходу зi стану |
|
|
|
|
|
|
γn мож а пi рахувати як iмо- |
|||||||||||||||||||||||
меншi значення енер i¨. |
n |
ужиттястани,атомащо¹ |
|
|
|
дженомутобтостанiмають |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
íуижчими,збу |
|
|
|
|||||
Îñêiëüêè |
|
|
|
|
|
|
τn = 1/γn. |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
äî |
|
|
γn |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
íà |
|
|
числавизнача¹тьсяотонiв електромагнiтногоюсякдиницяiмовiрнiсть, то переходу,часжиттящо пропорц й |
|||||||||||||||||||||||||||
новноговза¹модi¨сутще йi,вiдтоiнтенсивностiмз |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
êâàçiñò |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
τn |
|
|
|
|||||||||||
|
|
|
|
|
à¹ìîíó,льовимияклишеануспонтоливзаннiайменшоюнямиперехполядиенерна.поляОчевидно,нижчii¹ю,.Коливеличинарiвнiщоотонивнаслiдокзалежитьдляос |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
wi→f |
виведеннi |
||
цiонарно |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
γ0 |
= 0, |
|||
åíåð |
|
|
|
|
|
випромiнюваннянарнийвихстанiвст .величиною:ормальноЦiкаво,щоможврахуванняздiйснити,квазiстацiонарякщо- |
||||||||||||||||||||||||
τ0 |
=iþ∞вважатиивнiстьквантацiкомплексною |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
була п опорцiйною до дельб з |
|
|
|
En |
→ En − ~γn/2. - |
|||||||||||||||||||
замiстьностiIнтенанiв |
|
|
|
|
|
|
|
|
|
|
|
|
урахуватункцi¨ |
|
|
|
|
|||||||||||||
|
|
дляймовiрностi перех ду заацiонарнiдиицю часу δ(Ef −E ), |
ó |
|||||||||||||||||||||||||||
виразконанну |
закону збереження енер i¨. Тепер, якщо приотрима¹мо,забезпчу |
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
врахуватиакийквазiствираз: |
|
|
|
|
|
|
стани, то |
|
|
|
|||||||||||||
|
|
|
äåëü - óíêöi¨, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
wi→f |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
∞ |
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
δ(Ef − Ei) = |
|
|
|
Z−∞ e |
|
(Ef −Ei)tdt |
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
~ |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
2π~ |
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
π~ Z0 |
|
|
|
|
~ |
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
= |
1 |
|
|
∞ cos |
|
Ef − Ei |
|
|
|
t |
dt |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
→ π~ Z0 |
∞ |
− |
|
|
|
|
|
|
|
|
|
~ |
|
|
|
|
||||||||
|
|
|
|
|
|
|
1 |
|
|
γf +γi |
|
|
|
|
|
E |
|
− |
E |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
e |
|
|
2 |
|
|
t cos |
|
|
|
|
|
f |
i |
t dt |
|
|
521 |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
