Vakarchuk_I_O_Kvantova_mehanika_Pidruchnik_B

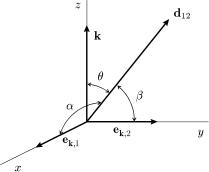
ис. 53. Напрямнi коси уси дипольного моменту

d12

iнтенсивностiатричнийЦейвиразелементвиявля¹дипольногоперповнуторавипромiнювання

аналогiюдипольногозкласичною.моментуУкласичномуормулою. виразiдля

тьсяiдносоменкласичномуовийомпонентоюiБорачастинкиое

d12

-

ì÷èñ

.розкладiiцi¹нт,Треба.Цезкляклишецiлкчастàправило,дупам'ятати,тиуядзмiнююпишуджуФур'¹¹тьсщокласичноговипромiнюванняповнiстюнез4/3,класичномумежахпринципом2/3,дипользамiтомуiдпоíю¹огощо

â нашому випадку вiд 0 д

(−∞, ∞),

матричнимЯкбачимо,елементомхарактер випромiнювання∞.

âè íà÷à¹òüñÿ

можливi лише тодi,.Отже,оли

ïî

глинання вiтла

d12 = er12

âiä iííèé âiä íóëÿ íå äëÿ áóäü- êèõ

ñòàíiâ . Çðîçóìië , ùî

r12 6= 0

âîãî é

стназиваютьщоанiвдлякладаютьстого,щоб наатричнийхв льовiелементункцi¨ляторапочатк. Сукуп

óì â,

|1i

|2i

Займемось

ñòü

êiнцевог

правиламигдинатиармонiдбчного.руПочнемодипоосц ьнихзнайпростперех.недорiвнюзраху¹шо.

вавгомо

випадкуматричнийнулевi,операторiвдновимiрноготеперелементцимиправилакоор

r12

502x12 = r

2mω hn|ˆb+ +ˆb|n′i = r

2mω n√n′

+ 1δn,n′+1

+ √n′δn,n′−1o .

ження= n′

x12

=

h1|x|2i, äå |1i

= |n ,

осциляторнiпородженняхвильовiзнищенняункцi¨.зВикосциляторно¨ориста¹мо задачi:зобра

| i

|

i

-

~

~

Обчислимо матричний2 = nелемент′, l′, m′

= Rn′,l′(r)Yl′,m′(θ, ϕ).

| i

|

i

p12 = h1|ek,αpˆ

|2i =

mω

h1|ek,αr|2i =

mω

i

i ek,αr12.

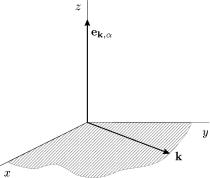
озглянемо спочатку квàíò, що поляризîâàíий уздовж осi

(ðèñ. 54):

z

p12 =

mω

z12.

i

Çâiäñè

виплива¹, що

+ Bl,mδl+1,l′).

z12

= Rδm′,m(Al,mδl−1,l′

z12 6= 0 за умови

Нехай т пер отонm′випромiню¹тьс= m, векториl′ лянемо= l напрямку1.

îñi

±

ляризованого

z, òîäi âåê-

ïî ek,α åжатьсвiтла,уплощинiдиничнixy. îçã

поляризацi¨випадокциркулярноякого

òà

ek,+

ek,− визначаються ормулою:

1

повiднодиничнi вектори

ek,± = √

(ek,1 ± ek,2),

2

. Ç

(тобтоповiда¹

âçäî

осей омпонентунапрвiд-

ek,1

ek,2 íàïðямленi

x

y

æíèêó¹

-ê

çà àçîþ íà

−круговiй, оли x-компонента виперед

y

iπ/2

),

âiäïîâiä๠ëiâiéπ/2

yполяризацi¨:-к

вектора

зма¹кiнцямно

e−

= −i

леного вздовж осi

поляризацi¨,k

ÿì

ñòðiëêè. Çíàê

z,

ворот вiд x äî y пiде проти годинников ¨

му випадку

+

пр вiй круговiй

â öü

äèíå

уваеличинами,имо,що,вектораx-колиомпуве торномуичнiвiдствектори¹нцiалiвiдполяризацi¨y- омпоненти¹комплекнаπ/2íèìè.Çà

îäæ ¹ться множни

ˆ

A оператор Bk,α супро-

матричний,

ратор

ˆ+

множник

.

елемВ остнтiоч их виразах цеekприведеîï

ëèøå äîB замiни в матричномуe

,α

.

k,α

k,α

Теперpнас цiкавитьe

k,α

íà e

елемент

12

k,α

iy

2i

h1|ek,±r|2i = h1 x √±2

1

= √

h1|r sin θ cos ϕ ± ir sin θ sin ϕ|2i

2

1

hn, l, m|re±iϕ sin θ|n′, l′, m′i

= √

505

2

ïларомiнюваннi.меВласнийткiлькостiмоментлiнiйнорухукiлькостiполярзнульовоюзованогорухупроекцi¹юотонасвiтлаправиламдорiвню¹зню¹твiсьма виноситьс. При я-

ì

~

îòî

пошир

в площинi

z, m = 0:

åêöiÿ

менту iмпульсу отона наxy.вiсьДля

лово¨ поляризацi¨ про

-

òî

þназивають¹тьсяди,матричномупроекцiявипромiнювання.Ящозабопiдкормоменоненимиавилоелементiяютьсуâiäякiлькостi.дбосутн¹,Урахуваннярiнерухуiдповiднiикону¹ться,вiдбору,атомавiдповiднонаступнихквнази.

членiвтовiелектричневаютьсядо цьогКвантовiпеехозклаiдборудозволенимизмiндипольнеперех

z

±~

-

êi

ïàð

âèëальнимможливимиовихквантовимункцiй,пов'язанi.якчисломздлясиметрi¹юцентральнзадачi,гоможеполяiзокремазробитивизнача¹тьз

èðàç

ek,α. Тому загалом

ïiäiíòå

кiнцевий

то матричнийякщопочаткелементовий

стани ¹ с ерично-сим тричнимl. Íàïðèêëàä,

p12мутотожновиразi длярiвний нулевi. Сп

àâä , ïðè iíòå ðóâ

ííi

r â òî÷

уздовж

едновийi парагра )

правимо вiсь

поляризацi¨(д . попепарною

z

p12

ek α. При цьому ek,αpˆ|2

залежить

z

, ñò

|1

p12

(kr)

þ óíêö ¹þ

. Ôàçà

експонентибуденепар

âiä

z

k

ерпендикуля

вiрностейì

, оскiльки хвиль

вектор

¹

ктора

ральний

ороненiлижал дорiвню¹ня.Знятиоператорiдляймонуцю

зховуючитевекторного

рення. Пер мквантовихждибуа,мiжехiбанеппропорцiйнийтперехкимирноющовраховуючидiв,стауíàкцi¹юмитакстроговищiжйврiíàá

çлевiаборо p12

z

ˆ

до квадратà

потенцi-

àëó

V ÷ëåí,

p12 = −ih1|(kr)(ek,αpˆ)|2i.

507

добуткуми

[ek,α[rpˆ

]] = r(ek,αpˆ) − (ek,αr)pˆ,

розписали.Помножимойогоза цейправиломвираз розкриттяскалярнонаподхвильовийiйн го векторного

k,

костii використа¹моруху:(krозначення)(e pˆ) = (оператораk[e [rpˆ]])орбiтального+ (e r)(kpˆ)моменту,

êiëü-

k,α

k,α

k,α

àáî ïiñëÿ öèêëi÷íî¨(kr)(e перестановкиpˆ) = ([e

ˆ

ró)(мiшаномуkpˆ),

добутку

Lоператорiв]k) + (e

k,α

k,α

k,α

Отже, матричний(kr)(елементe pˆ) = ([ke

ˆ

r)(kpˆ).

k,α

] L) + (e

k,α

k α

p12. Передуñiì

ìà¹ìî

p12 = −ikh1|(nk,α L)|2

1

]перпенд

щини,данокдиничнийутворено¨вектор,векторамищоnнапрямлений= [ke

кулярно до пло-

k,α

k

k,α

у отже,дослiджуванийоператори,вираз,

входять

омутуютьзi скалярнихмiж собою:добуткiв, ùî

äî

виразi для

k òà ek,α. Перетворèмо тепер другий

вектори

~(k )(ek,αr).

Îñêiëüêè (kpˆ)(ek,αr) = (ek,αr)(kpˆ) −

kскладенiтe вза¹мно перпендикулярнi, то

k,α

(k )(ek,αr) = (kek,α) = 0

çà (ek,αr)(kpˆ) = (kpˆ)(ek,αr).

åíòi

Постави

ái

мету позбут сьомутматричному еле

ратора

ìпульсу

p12 îïå

нi. Для цього розглянемоpˆ àê, ÿê öå

зробиликатор:вдипольноìу наближен-

àêèéì

ˆ

pˆ2

−

pˆ2

508

[(ek,αr)(kr), Ha] = (ek,αr)(kr)

2m

2m

(ek,αr)(kr),

2

.

наш комутатор

ˆ

im

ˆ

èì ìè ìàëè

Перед −ö

~ [(ek,αr)(kr), Ha] = (kr)(ek,αpˆ) + (ek,αr)(kpˆ).

òîìó

ˆ

(ek,αr)(kpˆ) = (kr)(ek,αpˆ) − (nk,αL) k,

(kr)(ek,αpˆ) = −

im

ˆ

k

Тепер

[(ek,αr)(kr), Ha] +

(nk αL).

2~

2

обчислювалè),

де матричний елемент

ìåíту iмпульсу

|2i + 2 (nk,αL12),

h1|(kr)(ek,αpˆ)|2i = ìî− 2~

ωh1|(ek,αr)(kr

якогоМи пам'ята¹мооператора(i це вже неодноразовоˆ

ùî äëÿ áóäü-

L12

= h1|L|2i.

ˆ ˆ

ˆ ˆ

ˆ ˆ

ˆ

ˆ

ˆ

ˆ

h1|[f , H]|2i =

h1|f H − Hf |2i

= h1|f H|2i − h1|Hf |2i

=

ˆ

ˆ

ˆ

509

E2h1|f |2i − E1h1|f |2i =

~ωh1|f

|2i,

Остаточно, з урахуваннямω = −~òîãî,. ùî

E2

E1

k = ω/c, знаходимо:

mω

iω

µ, ν = 1, 2, 3 x1 = x

x2 = y, x3 = z. Справдi,

пдодальíî

p12

черезвходитьоператороператорелектричногоiмпульсу,а

кгоможнамоментусправдiпереписатиявноне

квадруперший-

µ,ν

X

µ

ν

1

h1|3x

µ

ν

− r

2

δµν |2i

=

ek,αk

x

X

h1|r2|2i

1

X

+

eµ

kν

δ

=

eµ

kν 1 Q 2

µ,ν

k,α

µν

3

3e µ,ν

k,α

h

|

µν | i

1 r2 2

1

X

µ

ν

àäæå

умова

+

h |

| i

ïîëÿ(e

k)âèì= àãà¹,

ÿêe ìèk

1çíà¹ìî,Q 2 ,

ùîá

поперечностi

k,α

k,α

h

|

µν |

i

3

3e µ,ν

(ek,αk) = 0. Уведемо вектор Q з компонентами

i тепер

Qν =

X

ekµ,αQµν ,

µ

mω

mω

mω2

äå

h1|(ek,αr)(kr)|2i =

(kQ12) =

(ikQ12),

µB = |e|/2mc:

e

випромiню

Остаточно, якщо врахувати iˆ

ˆчлен розкладу в

å øèé

µˆ =

−µB L

= 2mc

L.

Першийквадрупольнечлен

Iñï(k α) =

2πm2c3 |p12|2.

p12, ÿêèé

ми дослiдили в попередньому ïàðàãðà i, çíàõ äèìî:

p12

= −imω(ek,αr12) −

imω

(nk,αµ12)

mω

X

µ

ν

h1|Qµν |2 .

e

− 6e

µν

ek,αk

вання:Цим виразом визнача¹ться

iнтенсивнiсть ñïîнтанного

-

випромiнюваííÿ,

e2ω2

ювання: ць p12

му випвiдповiда¹дкускорочза

Другий

äî àíîê

визнача¹

ã

äèïâiäïîâiäà¹ëüíå

E1-перех ди.

íå -ïå

M 1

еходи. Нарештi, третiй додàáî çà

çà åëåê ðè÷-

члени

ìàãíiòóï

озкладу велич ни

E2-ïå åõ äè. Íàñ

p12

електричнi т

íi

IMñï1(k, α) =

ω4

äå

2πc3 |µ12|2 cos2 θ,

θ

кут мiж вектором

µ

пiдсумоватдинич им вектором n

iнтенсивнiстьрована за всiма кута

è òà

íа за всiма поляризацiями. Проiн-

Мiжментуневiдомих,3Миiншим,зiщойнобу

ñï12

4 ω4

2

k,α

IM 1

=

3 c3

|µ12| .

вiдрiзнялисеемоедньовiчнiвведенимиплутати¨хзаiндiйськiiндексамипозначендопомогомаеíþÿëòîïðiçíèõматктрераторачногокиарбвмагнiтногорiвняннях,.квадрупльногощодипольнмалимоментукiлькаго511-.