
Vakarchuk_I_O_Kvantova_mehanika_Pidruchnik_B
.pdf
гамiльтонiана атома
електронаˆ |
pˆ |
2 |
|
|
ç |
+полемU . Òóò |
|
магнiтногооперато а вза¹модi¨ Ha = |
2m |
||
пульсу електрон , |
|
|
pˆ оператор iм |
¹модЯк¨зовнiшньвiдомоядполяомкласично¨iншимиmалiбруваннямйогоелектронамимас,динамiки,U . потенцiальнавмиканняенерелекiя взаро-
мiною iмпульсу зар |
|
жен ¨ частинкиϕ = 0 d v A = 0 çäiéñíþ¹òüñÿä |
|||||||||||
пульсучастинкичастинки.Вiдповiдно iíþ¹ìîöü ãî |
квантовiй механiцi, деоператорзарiм |
||||||||||||
|
|
|
äî |
|
|
|
p − eA/c e |
||||||
|
îìó |
pˆ |
|
|
|
|
муна полipˆ − e(дивA/c. такожгамiльтонiанŸ16) атома в |
||||||
|
|
електромагнiтн |
|
|
|
|
|
|
|
||||
де оператор вза¹модi¨Hˆ ′ = |
1 |
|
(pˆ |
− |
eA/c)2 + U = Hˆ |
|
|
+ Vˆ , |
|||||
|
|
a |
|||||||||||
|
|
a |
2m |
|
|
|
|
|
|||||
|
|
ˆ |
|
|
e |
|
|
|
e2 |
|
|
2 |
|
З умови |
|
|
ïîëÿ |
|
|
|
|
|
|
||||
|
|
|
+ pAˆ ) + 2mc2 A |
. |
|||||||||
|
поперечностiV = − |
2mc |
(Apˆ |
||||||||||
торний потенцiал, виплива¹,divùîAоператори= 0, яка наклада¹ться на век-
|
|
|
|
|
|
|
pˆ A омутують: |
Тому операторpAˆ =âçà¹ìîäi¨−i~ A +атомаApˆ =ç−полемi~ div A + Apˆ = Apˆ. |
|||||||
|
амiльтонаˆ |
e |
|
|
e2 |
2 |
|
|
|
атома й åëåктромагнiтного поля за- |
|||||
|
|
||||||
пису¹моПовний операторувиглядi V = −mc Apˆ + 2mc2 A . |
|||||||
492буваються квантовi перех ди системиV ÿê збурення,атом плюспiд дi¹юполе якого. вiд- |
|||||||
|
ˆ |
ˆ |
ˆ |
|
|
||
|
H = H0 |
+ V |
|
|
|||
äå |
ˆ |
ˆ |
|
ˆ |
|
. |
|
Будемо розглядати операторH = H |
ph |
+ H |
|||||
|
0 |
|
|
a |
|
||
ˆ
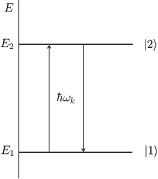
в дпНехайвiдниìиа¹моенератомiямиiз вибраними двома станами |1 óíêöi¹þромаг|2i ç
íiòíîãî ïîëÿ ç i¹þ E1 i E2 (äèâ. ðèñ. 52). Ñò åëåêò -
E...,Nk,α,... зада¹ться хвильовою
| . . . , Nk,α, . . .i.
ис. 52. Квантовi пер ди дворiвнев му атомi. |
||||||||
Почнемо |
ç |
квантового |
перех ду, |
унаслiдок якого |
||||
óíêöié |
|
|
|
|
|
|
||
ню¹тьстоюя отон iз хвильовим вектором k, поляриз цi¹ювипромiα ñ |
||||||||
ñòàí |
. Отже, нехай атом зн х дитьс |
â ñòàíi |
. Ïî÷àò- |
|||||
êîâèé ωk = kc |
системи з гамiльтонiàíîì ˆ |
|
|2i |
|||||
хвильових |
| i |
|
атома |
ïîëÿ |
|
H0 |
опису¹мо добутком |
|
à åíåð iÿ |
|
|
|ii = |2i | . . . , Nk,α, . . .i, |
|
|
|||
Кiнцевий стан |
|
E(0) = E2 + E...,N |
k,α |
,.... |
|
|
||
|
|
|
i |
|
|
|
|
|
|f i = |1i | . . . , Nk′ ,α, . . .i,
Ef(0) = E1 |
+ E...,N ′ |
,.... |
493 |
|
k,α |
|
|
Насв iцiкавитимеiншi числа народженняотонiв одного отона, коли Nk′ ,α = Nk,α + 1,
Nk′ ′,α′ залишаються тими ж, тому енер iя
(0) |
|
|
|
моперехЦе заIмовiрнiсть¹загальноюдiвакзванi¹процесквантовогодноEормулоюрозсiянняото= Eпереходуз+переходисвiтлаŸ56:E . за. одиницюПрикладом+ ~ω . часудворозрахову¹отонних- |
|||
f |
1 |
...,Nk,α, .. |
k |
|
|
|
|
2π |
|
|
|
|
|
2ç ó |
|
(0) |
|
|
(0) |
|
|
|
|
|
|
|||||||
Обчислю¹мовекторногоматричнийпотенцiаëóелементполяˆ |
|
ахуванням запису оп рато- |
||||||||||||||||||||||||||
ðà |
w →f = |
|
~ |hf |V |ii| |
|
δ |
Ef |
− |
Ei |
|
. |
|
|
|
|
||||||||||||||
знищення отонiв: |
|
|
|
|
|
|
|
|
A ÷åðез оператори породжåííÿ i |
|||||||||||||||||||
ˆ |
|
|
|
e |
|
|
|
|
|
|
|
|
|
|
e2 |
|
|
|
2 |
|
|
|
|
|
|
|
||
hf |V |ii |
= − |
|
hf |Apˆ |
|ii + |
|
|
hf |A |
|ii, |
|
|
|
|||||||||||||||||
mc |
2mc2 |
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
X |
2π~c2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
hf |Apˆ|ii |
= |
|
|
s |
ωk |
V |
|
|
h1|eik′r(ek′,α′pˆ)|2i |
|
|
|
||||||||||||||||
|
|
|
|
операторiв |
|
|
|
|
|
|
|
|
|
|
знищення, |
|
|
|||||||||||
|
|
k′α′ |
′ |
|
|
h |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
× |
h |
|
|
|
|
|
|
|
|
|
|
|
| |
ˆ |
|
| |
. . . , Nk,α, . . . |
i |
|
|
|||||||
|
|
. . . , Nk,α + 1, . . . Bk′,α′ |
|
|
|
|
||||||||||||||||||||||
|
+ 1 e− k′r(ek′ |
,α′pˆ) 2 |
i |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
h |
| |
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
||
Згiдно з правилами |
|
|
|
|
|
|
|
|
|
|
породженняˆ |
i |
|
|
|
|
|
ìà¹ìî: |
||||||||||
|
× |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
äi¨h. . . , Nk,α + 1, . . . |Bk′,α′| . . . , Nk,α . . .ii . |
|||||||||||||||||||||||||||
h |
|
|
|
|
|
|
| |
ˆ |
|
|
|
|
| |
. . . , Nk,α, . . . |
i |
= 0, |
|
|
|
|||||||||
. . . , Nk,α + 1, . . . Bk′,α′ |
|
|
|
|
|
|
||||||||||||||||||||||
Теперh. . . , Nk,α + 1, . . . |Bˆk+′,α′| . . . , Nk,α, . . .i = δkk′δαα′p |
|
. |
||||||||||||||||||||||||||
Nk,α + 1 |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
hf |Apˆ|ii = p12s |
|
π~c2 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
494 |
2 |
|
(Nk,α + 1), |
|
|
|
|
|
||||||||||||||||||||
V ωk |
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
E(0) |
òà E(0) |
знаходимо рiзницю |
|
|
|
|
|
|
||||||||||||||||||||
щоIз тихвнашомужеправилвипадкудi¨операторiвp äíî= 1 e− |
ikr |
(e pˆ) 2 . |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
12 |
|
|
h |
отоннихпороджпåрехоннядiвзнищення виплива¹, |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
| |
|
|
|
|
k,α |
| |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
ÄëÿIçäâиразiвоотоннихдля переходiвhf |öÿA2величина|ii = 0. â äìiííà âiä íóëÿ. |
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
f |
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
твТепер, |
|
|
|
|
(0) |
|
|
(0) |
= E1 |
− E2 + ~ωk. |
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
Ef |
− Ei |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
îчного перехознахозбираючидимоу за îтриманiдиницю виразичасу випромiнюваннямразом,для ймовiрносотонаi кваносòîà- |
|||||||||||||||||||||||||||||||||
|
(+) |
2π |
e |
2 |
2π~c2 |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
кiнцевближеннiопису¹тьсПереходимоднохвÿ äîèëüотонрозовоюункцi¹юперехглядуних процесукцi¹юдiв.поглинанняТеперпочатковийсвiтла встантомуатож |
|||||||||||||||||||||||||||||||||
ìà |
wi→f |
= |
~ |
mc |
|
V ωk (Nk,α |
+ 1)|p12| |
δ(E1 |
− E2 |
+ ~ωk ). |
|
|
|
||||||||||||||||||||
|
|
þ |
уваги, |
|
|
викладки, аналогiчнi |
|
|
|
E1 |
|
|
âèùå, |
||||||||||||||||||||
да¹тьсплiту |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
é åíåð i¹þ |
|
|
|
|
|
|
|
|||||||
причомуãî | . . . Nk α, . . . |
|
à åíåð |
|
|
E...,Nk,α,... |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
стану атома |
|
|
|
|
|
|
|
|
. Хвильова ункцiя |
|||||||||||||||||||||
|
я хв льовою |
|
|
|2i, åíåð iÿ E2. Кiнцевий |
òàí ïîëÿ |
|
|
|
|||||||||||||||||||||||||
|
|
|
÷èñëà îòîíiâ |
|
|
|
|
|
. . . |
|
N ′ |
|
|
|
, . . . åíåð |
|
E |
...,N ′ |
|
|
, |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
|
|
|
îñòi |
|
|
|
|
|
... |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
,α |
|
|
|
|
|
|
|
|
|
k,α |
|
|
||
лишаютьсяотоназчастотоюбеззмiн. езухвильN ′ татом= Nkтакого1 перехдодунаведенихбузникненняN ′ |
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
k,α |
|
|
|
|
|
|
α − |
|
, à ðåøò |
|
÷èñ |
|
k′,α′ |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
çà- |
|||||||
i беручиОпускаючидо промiжнiщоω , |
|
|
|
îâèì âåêò |
ðîì k, |
|
|
|
|
|
|
α. |
|
||||||||||||||||||||
|
|
|
|
|
|
k |
|
|
|
|
|
iнтенсивностi |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |p12| , |
|
|
|
|
|||||
õ |
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
h2|e |
kr |
(ek,αpˆ)|1i |
|
h1|e− |
kr |
(ek,αpˆ)|2 |
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
линаннямдля ймовiротона |
|
|
|
квантового пере- |
|||||||||||||||||||
запишемодудиницюостаточнийчасурезупогльтат |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
( ) |
|
2π e |
2 2π~c2 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
глинанняПерш |
− |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
~ |
|
|
|
|
|||
|
|
|
нiжсвiтлрозраà, ðозгховляньмоувати рiвноважнийвипромiнюваннястсистеми атомi495по- |
||||||||||||||||||||||||||||||
|
|
wi→f |
= |
~ mc |
|
|
|
V ωk |
|
Nk,α|p12 |
| δ(E2 |
− E1 − |
|
ωk). |
|
|
|
||||||||||||||||
плюслютноIмовiрнiстьполечорнрозпотемпературоюго iлаог., що атомT ,знаходитьсяякий реалiзу¹тьсяв станахв моделi абсо-
çàäà¹òüñÿ |
äië |
|
Больцмана: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|1i àáî |2i, |
||||||||||||
|
|
|
e−E1/T |
|
|
|
|
|
|
|
|
e−E2/T |
|
|
|
||||||||||||||||
|
ñóìà |
|
|
|
|
|
ñòàíiâ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
ρ2 |
= |
|
|
|
|
|
|
|
, |
|
|
|
||||||||||||
де статистична ρ1 |
= (ñóìà |
|
|
, |
|
|
|
|
|
|
|
|
Z |
|
|
|
|||||||||||||||
|
|
|
|
|
Z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
En/T |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
линаннямькостi перехотона)дiв повтудèннi бутиназадрiвними:(тобто |
||||||||||||||||||||||||||
зУвипромiнюваннямрiвн важному станiпогкiZ = |
e− |
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
X |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
(+) |
|
|
|
( |
|
|
) |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
балансупереходiв. З урахуваннямтпризаiнi явнихчисел |
||||||||||||||||||
Цеотонiв¹акдлязванаймовiрностейумовадетальвиразiв кваíтовихого |
|
− |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
ρ2w |
→f |
= ρ1wi→f . |
|
|
|
|
|
|
|
||||||||||||||||||
|
|
ðiвноважнi |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
Nk,α на середнi |
значення N k,α ця умова да¹ |
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
àáî |
|
|
ρ2(N k,α + 1) = ρ1N k,α |
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
1 + 1/N k,α |
= ρ1/ρ2, |
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
E2−E1 |
|
|
|
|
|
|
|
|
||||||
Ураховуючи закон |
збереженнясеред ер i¨ |
. |
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
T |
|
|
|
|
|
|
|||||||||||||||||||||||
|
1 + 1/N k,α |
= |
|
e |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
~ |
|
|
|
|
номузнаходимостанi:явний вираз для |
|
|
|
|
|
|
|
|
|
|
числа отонiв у, рiвноважостаточно- |
||||||||||||||||||||
|
|
|
|
|
íüîãî E2 − E1 = ωk |
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
N k,α = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
~ωk |
/T |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
ормула Планка. Повна середняe åíåð− 1iÿ ïîëÿ |
|
|
|
||||||||||||||||||||||||||||
кууму |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
E áåç åíåð i¨ âà- |
|||
E0 äîðiâíþ¹ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
V |
∞ |
4πk2~ω |
|
|
||||||||
496 E − E0 |
= |
|
|
|
~ωk N k,α = 2 |
|
|
|
Z |
k |
dk |
||||||||||||||||||||
k |
α |
(2π)3 |
|
e~ωk /T |
|
1 |
|||||||||||||||||||||||||
|
X X |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
− |
||||||||

а розрахована на= |
îπ2c3 |
Z |
|
e~ω/T |
|
|
1 dω, |
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
V ~ |
|
∞ |
ω3 |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
äèíèöþ |
îá'¹ìó |
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
− |
|
|
|
1900 |
|
|
|||||
де спектральна |
|
|
|
|
|
|
− |
|
|
|
|
∞ |
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
i¨= випромiнюванняu (T ) dω, |
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
E |
|
|
E0 |
|
Z0 |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
густиíà åíåð |
|
|
ω |
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
V |
|
|
|
|
|
|
|
|
|
|
|
|
|||
тбувНi1900Це |
|
|
|
|
|
|
|
|
uω (T ) = |
~ω3 |
|
|
1 |
|
|
|
. |
|
|
||||||||
|
|
|
|
|
|
|
|
π2c3 |
|
~ω/T |
|
|
|
|
|
||||||||||||
ами,iецькогоприпу¹окутаенерстити,i ормула,навiвiзичногоiя щодного¨¨енерякуведеннятоквантiяариспершевипромòâà14пропорцiйнанаписав.грудняДлявипромiнювання¨¨доведенняМаксiíþ¹òüñ й Плачкуглистоти,éíøòвiнкаа¹тьсязасiдан19змушежовтняêâàíèéÿõ- |
|||||||||||||||||||||||||||
|
|
(çíà |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
e |
|
− |
|
|
|
|
|
||
поглина¹¹мо, о |
|
|
|
|
|
|
|
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
α |
айнiвськуε = ~ω. |
||||
Öþ çíàмениту ормулу Пла ка, |
àê ñà |
|
|
ÿê |
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
iнтенсивностiбудьймовiрностi-хто . |
квантових перехпiдсумуватичокдiвпоглинанотримазади |
|||||||||||||||||
íицюя свiтлаТеперасу2,.зна¹обчислимоЯкщотеперзнайденi |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
E = mc |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
увазi граничнийвiд пiдсумовперехiдóâàííÿ |
|
|
k до iнте рування, маючи на |
||||||||||||||||||||||||
âñiìà |
|
w ± |
) |
|
помножити на квант енер i¨ ~ |
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ωk |
çà |
|||||
|
хвильовими векторами |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
→f |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
- |
|
÷евид о,чоккiлькiсть) атоменерза |
i¨,диницющополяризацiямивипромiню¹часу: (зна, |
ìè + ) àáî |
||||||||||||||||||||||||
Перейдемо |
|
|
|
|
|
|
|
X X |
(±)çà~ |
|
|
dE |
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
dt . |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
w →f |
ωk |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
k |
|
|
α |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
V → ∞: |
X |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
dE |
|
|
|
V |
|
|
|
( ) |
|
~ |
|
|
|||||||
системиПереходимокрдивiíàò:òå ðàëi |
за хвильовими |
± |
|
|
|
|
|||||||||||||||||||||
|
|
|
|
Z dk α |
|
векторами до с ерично¨ |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
dt |
|
= |
|
(2π)3 |
wi→f |
ωk . |
|
|
|||||||||||
32 I. О. Вакарчук |
dE |
|
X |
|
|
|
|
|
V |
|
|
|
∞ |
|
2 |
|
(±) |
~ |
497 |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
Z dΩ (2π)3 |
Z0 |
|
|
|
|
|||||||||||||||||
|
|
|
|
dt |
= |
α |
dk k |
|
wi→f |
ωk, |
|
||||||||||||||||

випромiнюванняноюdΩ полярелемезацi¹ют тiлесного(поглинання)кутасвiтла. Визначимояк кiлькiстьтеперенерiнтенсивнiстьi¨ iз зада-
÷àñó |
α, що випромiню¹ (поглина¹) атом за одиницю |
|||||||||||||
t диницю тiлесного кута Ω: |
|
|
|
|
|
|
|
|||||||
|
( |
± |
) |
|
V |
∞ |
2 |
( |
± |
) |
~ |
|
|
|
|
|
|
âèïðомiнювання |
|
|
|
|
|||||||
Отже, iнтенсивнiсть |
Z0 |
dk k wi→f ωk. |
|
|
||||||||||
|
Ik,α = |
(2π)3 |
|
|
||||||||||
(+) |
|
|
V |
|
∞ |
|
|
2π |
|
|
e |
2 |
2π~c2 |
|
Ik,α |
= |
|
|
Z0 |
dk k2~ωk |
|
|
|
|
|
|
|||
|
(2π)3 |
~ |
mc |
V ωk |
||||||||||
Ç âä êè |
× (Nk,α + 1)|p12|2δ(E1 − E2 + ~ωk). |
|||||||||||||
âàííÿ в цьомуδ- ункцi¨виразiта викону¹мозурахуваннямелементарно,того,що k = ωk/c, iíòå ðó-
|
|
(+) |
e2ω2 |
|
|
2 |
|
|||
де частота переходу |
|
|
|
|
|
|
||||
2πm2c3 |p12| (Nk,α + 1), |
||||||||||
|
Ik,α = |
|||||||||
|
|
|
|
E2 |
|
|
E1 |
|
||
Аналогiчно iнтенсивнiсть поглинання |
ñâiòëà |
|||||||||
|
|
|
ω = |
− . |
||||||
|
|
|
|
|
|
~ |
|
|
||
|
|
( ) |
|
e2ω2 |
|
|
|
2 |
||
мiнювання,Поглина |
ñâiòëà |
Ik−,α |
= |
|
|p12| Nk,α. |
|||||
2πm2c3 |
||||||||||
|
вiдсутн¹ |
|
|
|
|
|||||
|
|
|
|
Ik(−,α) = 0, ÿêùî êiëüêiñòü îòîíiâ ïîëÿ |
||||||
випромiнювантобтодíя,ак,якщоiнтенсивнiстьцьомуполевипадперебува¹яêогоiсну¹восновномуi ма¹ назвустанiспонтанного.Випро- |
|||||
Nk,α = 0 |
|
ñï |
|
|
|
|
(+) |
e2ω2 |
2 |
|
|
|
|
|
|
|
- |
àсереднiжаючигнiтногонуля.Ценаквадратичнiполязабезпечу¹те,щоотониосновномувiдхиленнявза¹модiювiдсутнi,тобтозавдякиеëектронавакуумномулем,напруженiснуваннюзпстейанiлюктувiдмякаелекiн¹ |
|||||
498нiацiй,тромНезввiд |
Ik,α |
= Ik,α = |
2πm2c3 |
|p12| . |
|
причиною спонтанних квантових перехоптичдiв. Число |
Nk,α |
|
|
|
||||||||||||||
ñëiäîê |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
-, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
спектральнiпоглинаенераториотонiв,глинаютьпоглядраунгоiнтенунаняiз.- |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
çâàíiню¹омiнювання, |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
перший |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
ëНасправдi,iнад, |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
квантовi. икНатакСонцяхi¨.вип |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
випром |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ëüíéåðèiñó |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
åíåð |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
íöÿñ, íàï |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
ìî¨ |
|
|
|
|
|
|
|
|
|
ëiíi¨ò÷èâîíàзаситут¹юердякивипрностiПовернiмосьвiпоглинаннязабжжемiжлсамоякомувипромiнюютьвипромiнюваннянi¨роня¹1. вання:Здавалосьймовiрiснувапрацюютьдоатомiвумовиаджеiстюби,атомнихотонидетальнатмлазеризумовлю¹.атомисзгляньто¨перiîãспектратмлина¹осiндукованеСбала |
|
|
|
|
|
|
||||||||||||
|
|
атомних вз ¹модiй, виник ¹ перерозподiл |
|
|
|
ùî |
||||||||||||
випромiнюються, по всьому спектру. У цьому й |
поляга¹ суть ме |
|||||||||||||||||
ханiзму утворення аунго ерових лiнiй |
2 |
. |
|
|
|
|
|
|
|
|||||||||
|
|
Ÿ 62. Електричне |
д польне випромiнювання. |
|
|
|
||||||||||||
зглянемо |
|
|
|
отриманi |
âèð çè äëÿ |
|
|
|
|
|
||||||||
|
|
|
Прав ла вiдбору |
|
|
|
|
|
|
|
|
|||||||
âèïðîмiнюваннядокладнiшет поглинання свiтла. Для цього iнтенсивностейдостат ь - |
||||||||||||||||||
|
|
вираз для iнтенсивностi спонт нного |
|
|
|
|
|
|
||||||||||
аналiзуватисп , якому зосередимо |
увагу |
íà матричному елементiвипромiнювання |
||||||||||||||||
Ik,α |
|
|
|
|
|
|
|
|
|
|
|
|
p12 |
. Íàñ |
||||
цiкавит ме передусiм дiлянк довжин хвиль |
|
|
|
|
||||||||||||||
виразлю¹ й |
|
|
|
|
|
|
|
|
|
|
|
що цьомуункцi¨,яквипадкухоп- |
||||||
|
длядиму частинуспектра. Виявля¹ться,λ & |
1000 A |
|
|
|
|||||||||||||
|
|
p12 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
äè ðàêöiéíi |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
íà |
яких обчислюютьсзначноякмат ичнiощу¹тьселементи.Дiйсно, хвильовi |
|
|
|
|||||||||||||||
|
|
вiддалях порядку розмiрiв |
|
p12 |
|
|
|
|
|
|
||||||||
íóëÿ |
|
|
|
|
|
|
|
атомалим:помiтно вiдмiннi вiд |
||||||||||
експо енти |
|
|
|
|
|
|
|
a 1 A. Тому показник |
||||||||||
|
|
e− kr, |
а входить у p12, |
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
2π |
|
|
|
3 |
|
|
|
|
|
|
|
когоспектрiздобувшиа21 |
|
kr ka = λ a 10− |
|
. |
|
|
|
|
|
- |
||||||||
чавМеханiзмЙозенаенняунiверситетука.вiдомийосвiтуедрiФра укра¨,нгоеоретично¨.вивчаверняськийратки,(1787спектрираунгастроiзики1826)поясниплатаiзикеровихíåòâ наявнiстьАстрономiчнiйБ.мецькийТСолiнiй. Бабiйця, темнихупершеа(1936iз¨хнюобсерваторi¨к,1993),лiнiйзастосувавякий,тонкякийсамостiйносонячномуструктурЛьвiвсьпрацюдля¨х |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
499 |
32* |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|

Отже, ми ма¹мо змогу розкласти експоненту в ряд: |
|
||||||||||||||
λрозкладу:ментУ1точно,цьомуA à kríåïà 1 |
õiäíî |
|
|
kr + |
|
|
|
випромiнюван |
|
||||||
У результатi |
|
e−ikr = 1 |
− |
· · · |
. |
|
|
|
|
|
|||||
p12 |
= h1|(ek,αpˆ)|2 − ih1|(kr)(ek,αpˆ)|2 + · · · . |
|
|||||||||||||
Зрозумiло, що у випадку рент енiвського |
|
|
|
|
|
я,данколи |
|||||||||
|
|
|
|
|
|
iç |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
óватилишеядцей.першимматричдоíий елеом- |
|||||||||
|
ðаграозкладаючи, необi ми обмежимосьекспонентрозрах |
|
|
|
|
|
|
|
|||||||
намПроведеормул:ряд простихp12 = h1|ek,αpˆ |
|2 . |
|
|
|
|
|
|
|
|||||||
|
|
перетворень |
|
|
|
використанням вiдомих |
|||||||||
|
p12 |
= h1|ek,αpˆ|2i = ek,αh1|pˆ|2i, |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
ˆ |
|
|
ˆ |
|
|
|
Скориста¹мось1 pˆòèì,2 |
=ùî 1 mˆr˙ |
2 = |
1 m |
rHa − Har |
2 . |
|
|||||||||
h | | i |
h | |
| i |
h | |
|
|
|
|
|
i~ |
| i |
|
||||
à |
|
ˆ |
|
|
|
|
|
|
|
, |
|
|
|
|
|
|
h1|rHa|2i = h1|r|2iE2 |
|
|
|
|
|
|||||||||
ˆ |
|
X |
|
|
|
|
|
|
X |
|
|
||||
|
ˆ |
|nihn|r|2i = |
|
|
|
Enh1|nihn|r|2i |
|||||||||
h1|Har|2i = |
h1|Ha |
|
|
|
|||||||||||
|
|
n |
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
X |
|
|
|
|
|
|
|
|
|
|
|
|
|
Òîìó |
= |
Enδ1,nhn|r|2i = E1h1|r|2i. |
|
|
|||||||||||
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m |
|
|
|
|
|
|
|
|
|
mω |
|
|
|
де матричний елемент îïератора координати |
|
електрона |
|
||||||||||||
|
|
||||||||||||||
|
h1|pˆ |2i = i~ (E2 |
− E1)h1|r|2i = |
|
i r12, |
|
||||||||||
500 |
|
r12 = h1|r|2i. |
|
|
|
|
|
|
|
|
|
||||
Уведемо оператор дипольного моменту електрона |
|
||||||||
|
|
|
ñï |
|
|
ω4 |
|
2 |
|
Отже, тепер |
|
|
|
|
d = er. |
|
|
||
|
|
|
|
|
|
mω |
|
|
|
а iнтенсивнiсть спонтанногоp =âèïðомiнюванняd e , |
|
||||||||
|
|
|
|
12 |
|
ie |
12 |
k,α |
|
ñï |
|
ñï |
|
|
|
|
|
|
|
|
|
|
ω4 |
|
|
2 |
2 |
||
íèìментуМи ибачимо,випозгпелянемо |
|
Ik,α = 2πc3 |
|d12ek,α| . |
|
|||||
ðектрона,ехомiнюванням,дамищовипромiнювавона.томузалежитьвiдповiднiак ííÿ,випромiнюванняпiдсумованеелектричногоквантовiперехзаназиваютполяризацiями:диполüíîãîдипольìî- |
|||||||||
|
X |
|
|
|
|
|
|
|
|
Уве емо напрямнi косинуси |
|
|
вiдповiдно до рис. 53, вибираючи вiсь |
|||||||||||
|
|
|||||||||||||
Ik = Ik,α = 2πc3 |
|d12ek,1| |
+ |d12ek,2 |
| . |
|||||||||||
|
α |
|
|
|
|
|
|
|
|
|
|
|
|
|
z уздовж k: |
ñï |
|
|
|
|
|
|
|
|
|
|
|
|
|
ра):Використа¹мо |
= |
ω4 |
2 |
2 |
α + cos |
2 |
β). |
|
||||||
Ik |
2πc3 |d12 |
| (cos |
|
|
|
|||||||||
|
властивîñòi напрямних косинусiв (теорема Пi аго- |
|||||||||||||
|
Ikñï |
|
ω4 |
|
|
|
|
|
|
|
||||
äå êóò |
= |
|
|d12|2(1 − cos2 θ), |
|
||||||||||
2πc3 |
|
|||||||||||||
|
\ |
|
|
|
|
|
|
|
|
|
|
випромiПро íюваннятеру¹мозацейодиницювираззачасукутами. i знайдемо повне спонтанне |
|||||||||||
Iñï |
θ = (k, d12). ñï |
ω4 |
|
ω4 |
8π |
|
|||||
(ω) = Z |
dΩIk |
= 2πc3 |d12|2 Z |
dΩ sin2 θ = |
|
|d12|2 |
|
, |
||||
2πc3 |
3 |
||||||||||
|
|
|
Iñï(ω) = |
4 ω4 |
|d12|2. |
|
|
|
501 |
||
|
|
|
3 |
|
c3 |
|
|
|
|||
