
Vakarchuk_I_O_Kvantova_mehanika_Pidruchnik_B
.pdf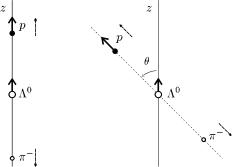
операторомiмпуè позначенольсiвчастинокповоротунапрямки0-.частинкинавколоспiнiâ системiчастинок,осi центраштрихованимимас.Суцiльниминапстðÿìêèiëêà- |
|||||||||||||||||||||||||
|
с. 37. озпад Λ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
y íà êóò θ: |
|
|
|
|
|
|
||||||||
|
Λ0 ′ |
|
y |
Λ0 |
|
|
|
|
cos 2θ |
|
sin 2θ |
|
|
1 |
|
|
|
|
|
||||||
|
= Rˆθ |
i |
= |
− sin |
θ |
|
θ |
|
|
|
|
|
|||||||||||||
|
| |
i |
|
|
| |
|
|
|
2 |
cos 2 |
|
|
0 |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
àìïëiòóäà éì |
|
âið |
îñ- |
|||||||||||
( |
b) sin |
θ . Îòæ |
повна |
θ äîðiâíþ¹ a cos |
θ |
à |
|
||||||||||||||||||
éìîâ ðíiñòü |
òîãî, |
що протон вилiта¹ пiд |
|||||||||||||||||||||||
|
|
|
= |
|
cos |
2θ |
θ |
|
= |
|
1 |
cos |
|
θ |
|
|
|
0 |
sin |
θ |
|
||||
|
|
|
|
|
− sin |
2 |
|
|
|
0 |
|
|
2 |
− |
1 |
|
2 |
|
|
||||||
спiномЗвiдсиуверхвиплива¹,=ïiä |кутом↑i cosùî |
θ |
− | ↓i s n |
θ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
2 |
2 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
ампл туда ймовiрностi вильоту пр тона зi |
||||||||||||||||||
тi того, що протон |
èëiò๠|
кутом |
2 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
− |
|
|
|
|
|
|
|
|
|
|
|
|
θ çi ñïiíîì óíèç, äîðiâ |
þ¹ |
|||||||||||
|
2 |
å, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
кутом |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
θ äî îñi z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
2 |
|
2 θ |
|
2 |
|
|
2 θ |
|
|
|
|
|
|
|||
312 |
|
|
w(θ) = |a| |
cos |
2 + |b| |
sin |
|
|
. |
|
|
|
|
|
|
||||||||||
|
|
2 |
|
|
|
|
|
|
|||||||||||||||||
Пiсля елементарних перетворень
äå |
|
|
w(θ) = A(1 + B cos θ), |
|
||
|
|
a |
2 + b 2 |
a 2 |
b 2 |
|
|
визнача¹A = | | |
кутовий| | , розподiлB =ï |
| | |
− | | . |
||
Ця ормула |
|
|
2 |
|
ротонiв у реакцi¨ розпаду |
|
|
|
|
|
|a|2 |
+ |b|2 |
|
0 |
|
|
|
|
ΛОскiльки-ч стинкивеличина.Експериментально вимiррушенняийкое iцi¹нт B = −0.63 |
||||
простоня àрностi. Справдi,B розпад= 0, ìà¹ìî ï |
закону збереж н- |
|||
|
|
|
|
å ¹. |
|
|
|
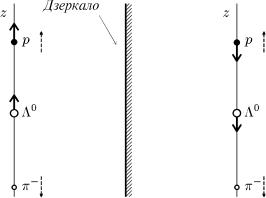
îзпадузiзiспiном уверхниз (дивц |
|
рис. 38).дзеркальне |
вiдображення-частинки¨¨ |
|
||
6 |
Λ0 |
|
|
|
ис. 38. Стани спiн уверх а спiн униз ¹ дзеркально вiдображеними. |
|||
сво¨ напрям якимина протилежнi. |
вектори напр ленi перпен |
||
Нагад ¹мо, що при акому дзеркальному вiдображеннi поляр |
|||
íi âå òîðè, |
¹ iмпульси частино , не |
ñâî¨õ íà |
|
ïðÿìêiâ, à àêñiàëü |
|
¹ спiни частинок, змiнюють |
|
дику ярно до дзеркала,вектори,напрямякимизмiнюють |
ÿрнi вектори, а |
||
аксiальнi вектори |
не змiнюють. Здавалось би, що |
ïëiòóäà ðîç- |
|
0
падувiдповiднiΛ -частинкиймовiрностiдзеркалi¹рiвними,такЯкщож за величинзмiнюютьполдорiвню¹ a i |a|2 = |b|2. Однак, як бачимо,313
експеримент свiдчить |
|
iíøå. Ñ ìåòði¨ |
|
правого не |
|||
iсну¹. Чи означа¹ це, що в дзерк лi закони ¹ iншими? |
Нi. Просто |
||||||
ми не врахували, що |
Ï |
ðîäà |
чить себе лiвогодзеркалi |
íå ëèøå ç |
|||
Îòæå, içè÷íi |
они пчастинок,цьому не змiнюються, якщо, крiм опе |
||||||
д ми : електржними |
|
барiонними, лептонними, а |
àê |
|
äèâíiñòþ. |
||
|
ñïiíàìè |
|
à ùå é |
|
|
çàðÿ |
|
iíâàðiàíòíiñòüпротилцi¨змiíувервсiхi¨ знакiвчними,здiйснитизарядiвопернацiюпротилежнiзарядовогопротилежними.Цеспракяжзванаення, тоб |
|||
òî |
P |
|
|
|
Ÿ 36. 5Матрицi. |
операторiв повороту для |
CP - |
цiкментуолиОбчислимомоменткiлькостiзастосуваньклькосрухуявномурухуматрицiвиглядiдорiвню¹операторiвматрицiоператорiвповоротуj дляпроекцiй= 1випадкумоцi,
iзотопаний¹авихмоментакводнюжiмпульсуотон,(дейтронрiвноюхчатбовмнiйспiн),основомпонентарiвнийомуядернiйстанi)~диницi,.Вониiзицi.Спiн,.маютьма¹Наприкларiвнийдрочастинокцiлуважкогодин,низкувлас-
âêìàдваазусоюIззначення,¹загспокою,напрямокальногоне¨хвиразутрирухуну.zЦе-зiлевi,кдляшвидкiстюпов'язаноiсну¹ненульовихвидiленаспiнузсвiттим,матричних.отвiсьщонадляу набува¹просторi,елементiвлишеякаiз
hзнаходимоj, m + 1|Jˆ+|j, m |
= ~p |
|
|
|
|
|
|
, j = 1 |
m = 1, 0, −1 |
||||||||||
j(j + 1) − m(m + 1) |
|||||||||||||||||||
|
iншого |
|
|
|
|
|
|
|
|
|
CP |
|
|
|
|
|
|||
любовсебе,тому,атовимiрнiсть5Якщонiмвiдомо,когосьеJ |
= ~ |
|
0 |
0 |
√2 |
|
= ~√2 |
0 |
0 |
1 |
. |
|
|||||||
|
|
|
0 |
√2 |
0 |
|
|
|
|
0 |
1 |
0 |
|
|
|||||
|
|
0 |
0 |
0 |
|
|
0 |
0 |
0 |
|
|||||||||
ˆ+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
залииникненнятжливо,йомусво¹скаралионi,вiдображiзпроiнварiантнiстьвродливенняю.проблемуiнварiантнiсть,Тгобтоводi,юнаквiн вида¹тьсзакохавзневаженуÿ саменев |
|||||||||||||||
ипов'язувавЕхо,Нарцисщо незакрозпадахйогоБогисксумнiву |
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
ã |
простору, як , |
|
|
|
|
ðîçâ'ÿçó¹ - |
|
|
|
íi ïðî áà |
|
||||||||
(див. Ÿ 3, Приклад 4),ливо¨ |
|
|
|
ÿê |
|
|
|
|
|
|
|
|
|
KL0 -ìåç íîì |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
èì. щитом,Легендарзвiриякя. .вже.кяк |
|
|
|
|
|
|
|
|
|
дзеркщолядуалiсвiт-користуючисьнасвогоне¨,дзеркалiщитвiдякогоiншу¹мiднпорушуiншлюдиiстоту |
|
||||||||||
|
|
|
|
|
|
|
ïîã |
|
|
|
|
|
|
|
|
|
|
||
|
Персейне малиупрямогоМедузiсилбачè. € |
|
CP |
|
|
|
|
|
|||||||||||
314м'янiлидзеркийСтародавнiмалаПерсейалом,.тако¨Виходить,абивiдтявстрахiтгрекiуникнутиголо |
|
|
|
|
|
|
|
|
|
|
|
||||||||

то виписаний ряд згорта¹ться i
|
|
|
1 |
0 |
0 |
cos ϕ + |
|
1 |
0 |
0 |
i sin ϕ + |
|
0 |
0 |
0 |
|
|
Rˆz |
= |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
|||||||
ϕ |
|
|
0 |
0 |
1 |
|
|
0 |
0 |
|
1 |
|
|
0 |
0 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− |
|
|
|
|
|
|
|
|
|
cos ϕ + i sin ϕ |
|
0 |
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Îòæå, |
|
|
|
0 |
|
|
|
|
|
|
|
1 |
|
|
0 |
|
|
|
|
|
. |
|
|
|
|
|
|
||||
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
0 |
|
|
|
|
|
|
|
0 |
cos ϕ − i sin ϕ |
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
eiϕ |
0 |
|
|
|
0 |
|
. |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Оператор повороту |
навколоˆ |
îñi0 |
|
1 |
|
|
|
0 |
|
|
|
|
|
|
|
||||||||||||||||
R |
ϕ |
= |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
0 |
|
|
e−iϕ |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ˆy |
|
|
|
|
ˆ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
e |
iθJy /~ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Rθ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
ˆ |
|
|
|
|
|
|
|
|
ˆ |
|
|
2 |
|
|
|
|
|
|
|
ˆ |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
! |
|
|
|
|
1 |
|
|
|
! + . . . , |
||||||||
|
= Iˆ + iθ |
Jy |
+ |
(iθ)2 |
|
Jy |
|
+ |
(iθ)3 |
|
Jy |
||||||||||||||||||||
|
~ |
2! |
|
~ |
|
|
3! |
~ |
|||||||||||||||||||||||
|
~ ! |
|
|
|
|
|
√2 |
|
|
|
0 −1 |
|
|
− |
|
|
|
|
|
−1 |
− |
|
|
||||||||
|
ˆ |
2 |
|
|
|
|
|
|
2 |
|
|
|
|
0 |
|
0 |
0 |
|
|||||||||||||
|
Jy |
|
|
= |
|
|
|
i |
|
|
|
|
|
1 0 |
|
|
|
|
1 |
|
1 |
0 |
|
1 |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
316 |
|
|
|
|
= |
|
|
1 |
|
|
0 |
|
2 |
|
0 |
|
. |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
−1 |
0 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
1 |
0 |
|
|
1 |
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
− |
|
|
|
|
|
− |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
2 |
|
|
|
|
|
− |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||


|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
ˆ |
|
|
3 |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
ˆ |
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
Jy |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Jy |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
+ |
|
|
|
|
(iθ)3 |
|
|
|
|
|
! |
|
|
+ |
|
|
|
(iθ)4 |
|
|
|
! + · · · |
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
3! |
~ |
|
|
4! |
|
~ |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
~ |
|
|
|
|
|
|
|
|
|
|
|
|
|
~ ! |
|
|
|
|
|
|
|
|
|
− |
|
|
|
|
|
|
0 |
0 |
1 |
||||||||||||
|
= |
|
Iˆ + Jˆy i sin θ + |
|
|
Jˆy |
|
|
2 |
(cos θ |
|
|
|
|
1) = |
|
1 |
0 |
0 |
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
0 |
1 |
0 |
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
−1 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
0 |
−1 |
||||||||||||||||
|
|
|
|
|
sin θ |
0 |
|
|
|
1 |
|
|
0 |
|
|
+ cos θ − 1 |
|
|
1 |
0 |
|
1 |
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
1 |
|
|
|
0 |
|
|
|
|
1 |
|
|
|
|
0 |
|
2 |
|
0 |
|
|||||||||||||||||||||||||||||||
i остаточно |
|
|
√ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
− |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− |
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
поворотуR = |
|
1+cos θ |
|
cos θ |
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
sin θ |
|
|
1−cos θ |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
Оператор |
|
|
|
|
ˆ |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
√ |
2 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
y |
|
|
|
навколо осi |
|
|
|
|
|
|
|
|
|
|
sin θ |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
sin θ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
θ |
|
|
|
|
|
|
√ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
√ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
− |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
1− cos θ |
sin θ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1+cos θ |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
−2 |
|
|
|
|
|
|
√ |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
ˆx |
|
|
|
|
|
|
|
|
|
|
ˆ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
iαJx/~ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Rα |
|
|
|
|
e |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ˆ |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
ˆ |
|
|
2 |
|
|
|
|
|
|
3 |
|
|
ˆ |
3 |
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Jx |
|
|
|
|
(iα) |
|
|
|
|
|
Jx |
|
|
|
|
|
|
|
(iα) |
|
|
Jx |
|
|
|
|
|||||||||||||||
|
|
|
= Iˆ + iα |
|
+ |
|
|
|
|
|
|
|
|
|
|
|
|
! + |
|
|
|
|
|
|
|
|
|
|
! + · · · , |
|||||||||||||||||||||||||||
|
|
|
~ |
|
|
2! |
|
|
|
|
|
|
|
~ |
|
|
|
|
3! |
|
|
|
|
~ |
||||||||||||||||||||||||||||||||
x |
|
|
|
2 |
|
0 |
|
1 |
|
0 |
|
|
|
0 |
|
|
|
1 |
|
|
0 |
|
|
|
|
|
2 |
|
|
1 |
|
0 |
1 |
|
||||||||||||||||||||||
|
|
|
0 |
|
1 0 |
|
0 1 |
|
|
0 |
= |
|
1 |
|
0 1 |
|||||||||||||||||||||||||||||||||||||||||
Jˆ2 = ~2 |
|
1 0 1 |
|
|
|
1 0 1 |
|
|
~2 |
0 2 0 |
, |
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
Jˆx |
! |
3 |
|
|
|
|
|
|
|
1 |
|
|
|
1 |
0 |
|
|
|
1 |
|
|
|
0 |
1 |
0 |
|
|
|
|
|
||||||||||||||||||||||||
318 |
|
|
|
= |
|
|
|
0 2 0 |
|
|
1 0 1 |
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
~ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
2√2 |
1 |
0 |
|
|
|
1 |
|
|
|
0 |
1 |
0 |
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||

|
å, ìî |
|
одночасно вимiрювати квадрати к жно¨ з |
|
|
|
|
|
юватиз проеяêцiйщо набува¹повниймоментзначеннядорiвню¹квадрат. Причомуомпонентос- |
||
проекцiйкiлькиОтжментудорiвжiмпульсу,на |
~ |
|
|||
ìî |
|
|
нулевi або |
( ~, 0, ~), то ¨¨ квадра |
|
|
|
|
~2 |
− |
|
ˆ |
ˆ |
ˆ |
овому.Т якщо взяти |
уваги, що |
|
|
|
|
|||
2 |
2 |
кожен2 ç äâîõ2, то iншихпринульдорiвнюватимезначеннi |
äíi¹¨ ç |
||
Jx |
+ Jy + Jz |
= 2~ |
|
|
|
|
|
|
а¹тьсвердзв'язанихпîверго. тiлахнею с ери ра- |
||
дiусаКласичнаŸ 37частинка,. Квантовещо вiльнообертаннярух |
~2 |
|
|||
моментiюa, пула¹кiнетичнусу, енер iю E = L2/2I, äå L класичний
|
|
вiдповiднрухуотрвохмоментèму¹мой жорсткоператiнерцi¨çàìiíîþенер.Цйi¨виразтако¨частиноквсистезнача¹.и,У |
||
|
називаютьер обертовоговипадкуротатором, |
|
|
|
квантовомуй |
I = ma2 |
|
|
|
ÿêó |
|
|
|
|
менту iмпульсу: |
|
L на оператор ìî- |
||
|
|
ˆ |
ˆ2 |
|
|
|
L |
|
|
HЦей гамiльтонiан опису¹ обертанH = íÿ.таких лiнiйних молекул, як |
||||
|
|
|
2I |
|
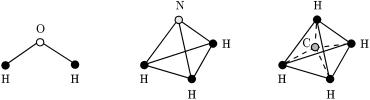
ченнями2, Oiâíi2, Nенерквадрата2, Cl2i¨, роттакорбiтатораисж. CO,льного39визначаються,.ЛiнiйнiHClмоменту(дивмолекули. рисякiлькостi.бачимо,39). . |
рухувласними зна- |
|||
320HдженняОбертова. енер iя складнiшихEl = ~2 lîá'¹êòiâ,(l + 1) як наприклад,-кратнемолекувласнiвиро-
2I
lвизнача¹= 0, 1, 2проекцiю, . . . . Енермоментуiя не залежитьiмпульсу:вiдма¹моквантового числа m, ÿêå
(2l + 1)
O, NH3, CH4 (див. рис. 40), так ж визнача¹ться через
|
|
ис. 40. Багатоатомнi молекули. |
|
||||
значення квадрат |
|
iлькостi руху та його проекцiй, як- |
|||||
ùî |
лядати обертан я |
ê |
молекул як |
ання твердого |
|||
òiëà |
жор тко закрмоментупле ими атомами. Модельобертко¨ дзи опису¹ |
||||||
й обертовi ступенi |
iльностi àòомних |
дер. У заг льному |
|||||
á |
âà åíåð iÿ |
|
âåðä |
òiëà |
|
ча¹ться амiльтонiаном, що |
|
îтриму¹ться з класичнîãî |
виразу длÿ åíåð i¨, çàï |
сано¨ випадкусисте- |
|||||
мi крозгдинат, осi яко¨ напрямленi вздоâæ головнèõ îñåé iíåðöi¨ |
|||||||
твердого тiла i обертаються разомвèçíàíèì: |
|
||||||
|
|
|
ˆ |
ˆ2 |
ˆ2 |
ˆ2 |
|
|
|
|
J1 |
J2 |
J3 |
|
|
äå |
|
|
H = |
2I1 + |
2I2 |
+ 2I3 , |
|
частинiавнiспiвввiдношенняголовнi |
длямоменкомпонентиiнерцi¨.моментуВиявл¹ться,кiлькостiщо переруху- |
||
|
I1, I2, I3 |
|
|
ˆ |
ˆ |
ˆ |
|
наядральтонiанквантовогодлящовiдiлькостiвиписатинеправил.омпУзмiню¹.загальноТомуописуруху,нентчислакнеможливо,омутсисзнайдених¨х¹,операторiвзрозумiло,отацi¨емiiститьвипадкуимуютькоорнерухомiйматричнихочадинатвнутрiшнiйобертовогонеоперацi¹ювласнiдля,розв'язатиякксистемiелезнажнобертесоличеннякгомеентiвментуклишеплека¹тьскорбiт,нкретногоякак.сногоя,альногоВипизн |
|||
J1, |
J2, |
J3 |
власнихнаприклад,вiдрiзняютьсомамiльтопряжанийзначеумоментузначеньправiйення,гамiспiнiаня-- |
Для повнiстю симетрично¨j аку зад чудзи и, к |
доволi просто. |
|
||
|
|
|
I1 = I2 = I3, |
|
|
|
~2 |
|
|
Прикладом |
|
молекуëà |
|
|
|
ìîæå áóòè |
Ej = 2I1 jметану(j + 1).CH |
|
|
21 I. О. Вакарчук |
|
4. |
321 |
|
