
Vakarchuk_I_O_Kvantova_mehanika_Pidruchnik_B
.pdf
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
hθ, ϕ|1, 0i = −r |
|
|
|
|
cos θ, |
|
|
|
|
|
||||||||||||||||||||
|
|
4π |
|
|
|
|
|
|||||||||||||||||||||||||
Функцi¨ |
hθ, ϕ|1, −1i = −r |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
8π e−iϕ sin θ. |
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Лeжандраhθ, ϕ|l, mi |
можна записати через |
ïðè¹äíàíi ïîëiíîìè |
||||||||||||||||||||||||||||||
|
|
|
sinm θ |
|
|
|
d |
|
m |
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
Plm(cos θ) |
= |
|
|
|
|
|
|
|
|
Pl(cos θ) |
|
|||||||||||||||||||||
d cos θ |
|
|
|
|||||||||||||||||||||||||||||
де полiном Лежандра= |
|
(2−ll! sinm θ d cos θ |
|
|
|
sin2l θ, |
||||||||||||||||||||||||||
|
|
|
|
|
|
)l |
|
|
|
|
|
|
|
|
|
|
|
|
d |
|
|
|
l+m |
|
|
|||||||
|
|
|
|
|
|
|
|
|
)l |
|
|
|
|
|
|
d |
|
|
|
l |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
sin2l θ. |
|
|
|||||||||||||||||
Тепер |
Pl(cos θ) = |
(− |
|
|
|
|
|
|
|
|||||||||||||||||||||||
2ll! |
d cos θ |
|
|
|||||||||||||||||||||||||||||
Якщо врахувати,hθ, ϕ|l, mi =ùî(−)l √2π s |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
2 |
|
|
|
(l |
|
|
|
m)! Pl−m(cos θ). |
||||||||||||||||||||||
|
|
|
eimϕ |
2l + 1 (l + m)! |
|
|
|
|
|
|||||||||||||||||||||||
|
òî÷íiñòþ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
óíêöiÿìè |
|
|
|
|
|
|
|
|
|
|
|
|
(−)l збiгаються зi с еричними |
|||||||||||||||||||
òî |
P m(cos θ) = ( )m |
(l + m)! |
P |
−m(cos θ), |
|
|||||||||||||||||||||||||||
|
l |
|
|
|
− |
(l |
− |
m)! |
|
l |
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
m eimϕ |
|
|
|
2l + 1 |
(l |
|
− |
m)! |
|
m |
|
||||||||||||||||||
Öi óíêöi¨θ, ϕ l,çm = ( )l+äî |
çíà |
êà |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
P |
|
(cos θ). |
|||||||||||
|
|
|
|
2 (l + m)! |
|
|||||||||||||||||||||||||||
h | |
|
− |
|
|
√2π s |
|
|
|
|
|
l |
|
||||||||||||||||||||
Yl,m(θ, ϕ), визначеними стандартно:
|
|
hθ, ϕ|l, mi = (−)lYl,m(θ, ϕ), |
|
|||||||||
|
|
|
|
eimϕ |
|
|
|
|
|
|
|
|
302 Y |
|
(θ, ϕ) = ( |
)m |
|
|
2l + 1 |
|
(l − m)! |
|
P m(cos θ). |
||
|
|
|
|
|
||||||||
|
l,m |
− |
|
√2π s |
2 (l + m)! |
l |
||||||

Випишемо у явному виглядi с еричнi ункцi¨ для l = 0, 1, 2, 3:
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
||||
|
|
|
Y0,0 |
= |
|
√ |
|
|
|
, |
|
|
|
|
|
Y1,0 = r |
|
cos θ, |
|
||||||
|
|
|
|
4π |
|
||||||||||||||||||||
|
|
|
|
4π |
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
Y1,±1 |
= |
r |
|
|
e±iϕ sin θ, |
|
|
|
|
|||||||||||||
|
|
|
8π |
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
Y2,0 |
= |
r |
5 |
(3 cos2 θ |
− 1), |
|
|
|||||||||||||||
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
16π |
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
15 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
Y2,±1 |
= |
r |
|
e±iϕ |
cos θ sin θ, |
|
|
|||||||||||||||
|
|
|
8π |
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
Y2,±2 |
= |
r |
15 |
e±2iϕ sin2 θ, |
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
32π |
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
Y3,0 |
= |
r |
7 |
(5 cos3 θ |
− 3 cos θ), |
|
||||||||||||||||
|
|
|
|
|
|||||||||||||||||||||
|
|
|
16π |
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
21 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
Y3,±1 |
= |
r |
|
e±iϕ(5 cos2 θ − 1) sin θ, |
||||||||||||||||||
|
|
|
64π |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
Y3,±2 |
= |
r |
105 |
e±2iϕ sin2 θ cos θ, |
|
|
||||||||||||||||
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
32π |
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
35 |
|
|
|
3iϕ |
|
3 |
|
знайдених ункцiй при |
|||||||||
Тепер¨iнвердекiлькаi¨, якслiвоператполяга¹проïåретвореннязамiнi |
|||||||||||||||||||||||||
|
|
|
Y3,±3 |
= |
r 64π e± |
|
|
sin θ. |
|
потенцiальна |
|||||||||||||||
|
|
|
iнверсi¨ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
операцiþ çäiéñ þ¹ |
|
|
|
|
|
р iнверсi¨ |
(x, y, z) (−x, −y, −z). Öþ |
||||||||||||||||||
ричних коордиíàòàõ |
àê |
|
|
|
|
|
|
|
|
|
|
|
|
|
ˆ |
|
|
|
|
||||||
îперацiя еквiвалентнаI. Легко бачити,замiнiункцiящокутвс е- |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
θ, ϕ |
π |
− |
θ, ϕ + π При цьому хвильова ункцiя |
π |
θ, ϕ + π l, m = |
|||||||||||||||||||||
l |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
h |
− |
| |
|
(−) hθ, ϕ, |l, m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
никоператоррнихзначень. Îòæå,l не змiню¹приоперзн |
ка,цi¨ iнверсi¨длянепарниххвильовадiста¹ множдля- |
||||||||||||||||||||||||
|
(−1) тобто хвильовакомуту ункцг |
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
, |
|
|
|
|
|
|
|
|
|
|
амiль¹тонiаном,парноюабобтонепарною. Якщо303 |
||||||||||||
поворотуженеру някцi¨iяпарностiUзберiга¹тьсянавколо(x, y, z.)Операцiю=îñi.UÓ(−цьомуx,iнверсi¨−y,випадку−z)можна, то говцяповоротiввластивiстьзглядатиятьякденнийпоальнимзакхвильово¨ |
|
|
îперацiюзбере |
бр женнямазують,площинi z íà êóò πзакнаступним дзеð |
âiäî- |
çàêвлеквiвалентнимионстивостiпiдкçаконбереженнязбережендляiзичних.щослабкихпарностiОдусистеакядзеркалiенертутвза¹мо.ŸОскiль35,iнту¨цiяi¨..абсолютнийiнту¨цiядiйТобтоСпiнони(диввiдлiвеак.наступнийпiдводитьжповсхарактер,неправезмiнюються,непарагзмiнюютьсяяк,цейвнапридосвiдзакониродiа)то2-. |
|||||||||||
порушу¹ться¹клад,н |
|
xOy |
|
|
|
|
|
|
|||
Пiвцiлi з ачення квантового числ , що визнача¹ квадрат ку |
|||||||||||
тового моменту, як ми бачили, не |
|
ÿ ïðè îðáiò |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
- |
|
|
|
|
|
|
|
|
|
|
|
- |
|
|
|
|
|
|
|
|
|
частинки,оординатазиваютьальномументмомент..дноМеЯкарж |
||
|
|
|
|
|
|
|
|
|
внутрiшнiй,спiномел |
||
анiзмякiйсiчностiсiстивчаальнимнийаснийишевонаинкиормуванняхвильдорiвнюютьзна¨¨яквнутрiшнiймоментом,.частинкрухДецимацiяцiлеово¨невласногоóiмпульсупросторi,.нóтобтокцi¨Умоментлевiхпiвцiлиха¹тьсцiйча.моментурозглядатиМоментсистемiчастинкия,тинкияккiлькреалiзуютьстознми¨¨остiприченьвжекiлькостiiмпулькiлькоординатназивають¨¨повнрухузазначали,ññòi,è.цеахстемiЦейрухурухучастинкотже,поворотахнаслiдокКрамерса,¨¨ |
|
||||||||||
хабоматиорбзв'язiмпульсу,щознару |
|
|
|
|
j |
|
|
|
|||
их частинок |
|
. Ùå . Êðî |
розглядав власний мех |
|
|||||||
Îäâi 2кинув цю моневiдомийель через телi, |
ùî ëiíié |
швидкiсть поверхнi |
àêî¨ |
||||||||
íi÷ |
|
й момент електрона як обертан я твердого тiла навколо осi. |
|||||||||
|
àê, çà ïîðà îþ Â. Ïàó |
Â. àéçå |
áåð à |
|
. À. |
âií |
|||||
Л. Пастер у 1848 роцi заува ив вiдсутнiсть симетрi¨ правого i лiвого на |
|||||||||||
èõ |
ìà þíêiâ |
брали за тра арет свою рукуПричина,переважно лiву, тобтоПочаткуонтури |
|||||||||
деяких рг |
|
сполуках бiологiчн х структур. Однак акi |
синте |
||||||||
зованi |
|
вiдтворюють цю сим трiю. |
|
отже, поляга¹штучноне iзич |
|||||||
них зак нах, зокрема, ¨¨ |
е можна |
ïð |
електр |
ìàãíiòíèì âçà¹ìîäiÿì, |
|||||||
були синтезоанiчнихлише лiвi структури, àáî |
процесi |
люцi¨ вони люкту |
|||||||||
ацiйноаводисполукиправою. |
|
|
|
|
|
|
|
|
|||
|
|
виявились у вигiднiших умо ах,писатиправi зникли, що й спостерiга¹мабо |
|||||||||
якi вiдповiдають за структуру молåêóë, |
òîìó ùî |
самого |
|
|
|||||||
сьогоднi. Ще |
дним доказом цього ¹ те, що первiснi |
художники для наскель- |
|||||||||
304 |
|
|
|
|
|
|
|
|
|
|
|

äçè |
|
áó |
бiльшою, нiж швидкiсть свiтла. Пiзнiше, |
|
1925 ðîöi, |
|||||
ðîíà |
власного |
êiëüê |
ðóõó. Ó |
|
|
àíiêó |
ñïií, |
|||
òèâiñòþ, |
як, наприклад, ¨хнiй заряд. Части |
жмехмати |
||||||||
öå óÿâ |
|
ня знову в iйшло до розгляду завдяки С. € |
ó |
|
òà |
|||||
Äæ. |
ленбековi, якi висловили припущення про наявнiстьдсмiтовiелек |
|||||||||
увiв у 1927 роцiмоментуВ. Па лi |
3 |
. |
частинок ¹ |
àêîþ æ âëàñ- |
||||||
Уважа¹ться, що спiн елемеостi |
||||||||||
|
ий нулевi, j = 0 це мезони,арнихзiскладнихквантовумоментучастинок ядро |
|||||||||
4He,ухуатомяко¨ визна4He тча¹тьсiншi.яПрочисломчастинку, квадр |
|
|
iлькостi |
|||||||
iвню¹ однiйспiу другiйвiсь . Пiд цим розумiютьнейтрон,говорять,мприкладсимальщо ¨¨значенняспiндо |
||||||||||||||||
проекцi¨ |
|
|
|
|
|
|
|
j = 1/2 |
|
|
|
|
||||
випадкуiншi,тарнi ч зiстискладнихки,як електрон,частинокzористовуючидиницяхпроа ~ |
|
|
~/2 |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
òîí,. Ñïií |
|
|
ìþîí,àþòü íåакiйтриноелемента- |
||||
|
|
|
|
|
|
|
|
|
омпонентHe, оператора. спiну для |
|||||||
Установимо вигляд ма риць к |
3 |
|
|
|
|
|
||||||||||
що матрицяj =é1/ãî2, âèê |
|
|
|
|
|
|
|
|
ати Ÿ33. Пригадаймо, |
|||||||
|
|
|
|
дiагональною:резу |
|
|||||||||||
|
|
z- омпоненти ¹ |
|
|
|
|
|
|
|
|||||||
Îñêiëüêè |
|
|
|
|
|
îâi |
= |
~mδj′j δm′m. |
|
|||||||
j′, m′ Jˆz j, m |
|
|
||||||||||||||
|
|
h |
| |
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
m = 1/2, −1/2, то матриця цього оператора |
|||||||||||||||
âií |
Jz = |
~/2 |
|
~ |
|
|
= 2 |
|
|
|
|
. |
||||
|
ˆ |
|
|
0 |
|
|
|
|
~ |
|
1 0 |
øЯкдзищоовкрутитьспобачивгеи,дiелементiвкрутитисщо.кричатьВласне,крутия,хлопбувя,-- |
||||
|
|
0 − /2 |
|
|
|
0 −1 |
|
|||||||||
щасливий,цяПригадаймогонятьiлосо3звiрОддзв,нбiгйогоою,щоаледоiлосопiзнавiдлишене¨,далi,разувiнiграшщвештавсярозумiтиняднубнасторожувавсящокупiйматии,жно¨мить,ненульi, завждивзагхопившидрiбницi,потiм.Вiнтам,некидав. значIзвертякзищойноде-от¨¨узавжди,гралисянапокинаприклад,увагидзиземлюåння матричнихвонайомудiтипочиналате,.щеi |
||||||||||||||||
òüñÿ, |
à÷à¹, ùîá |
áóâ |
хопле |
àëi âñå. . . I |
|
|
|
бачив и, як готуються |
||||||||
запустити дзи у, |
èé |
|
|
що тепер |
|
|
пощастить, . . . |
|||||||||
20 I. О. Вакарчук |
|
Франц |
Ка ка. Перетворення |
|
||||||||||||
|
Лiтературнанадi¹ю,енцiя Пiрамiда . Львiв, 2005. 305 |
|||||||||||||||
|
|
|
Оповiдання у п рекладi Iвана Кошелiвця. |
|||||||||||||

|
J можемо записати в такому вигëÿäi: |
|
|
|
|
|||||||||||||||||
Jˆy |
= |
~ |
|
0 1 |
|
|
~ |
|
0 0 |
|
~ |
|
0 1 |
|
|
|||||||
|
2i |
0 |
0 |
|
|
2i |
1 0 |
= 2 |
−1 0 |
|
||||||||||||
|
|
|
|
|
|
− |
|
|
|
|
|
|
|
|
||||||||
Оператор = |
2 |
|
0 |
−i |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
~ |
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
ˆ |
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
ˆ |
~ |
σˆ , |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
онатись, |
|
|
|
J = |
2 |
|
|
|
|
|
|
|
|||||||||
|
σˆ = iσˆx + jσˆy + kσˆz , |
|
|
|
|
|
||||||||||||||||
де матрицi Паулi |
|
|
|
|
|
|
||||||||||||||||
σˆx = |
0 1 |
|
|
|
|
σˆy = |
|
|
|
− |
|
, |
|
σˆz |
= |
1 |
0 |
. |
||||
|
1 0 |
|
|
|
|
|
|
i |
0 |
|
|
|
|
0 |
−1 |
|
||||||
Легко перек |
|
|
|
|
|
що ал ебра цих операторiв така: |
|
|
|
|||||||||||||
|
|
|
|
σˆx2 = 1, |
|
|
σˆy2 = 1, |
|
σˆz2 = 1, |
|
|
|
|
|||||||||
го моментуЩодопозначень,iмпульсуточастинкизвернемочастоувагупознате,чаютьщо опчерезатор власно |
|||
σˆxσˆy = iσˆz |
σˆz σˆx = iσˆy |
σˆyσˆz = iσˆx. |
|
т ве число |
|
ˆs, |
êâàí- |
j через s: |
|
|
|
|
~ |
|
|
Зауважимо, що |
îìáiíàöi¨Ïàˆs äð=ëióгогорσˆ .зом з одиничною матрицею |
||
|
2 |
|
|
|
|
|
ˆ |
утворюють повний н бiр. Це означа¹, що будь-який о ератор I |
|||
ìàктрицею |
|
ˆ |
|
тиякийвиглядiзобража¹тьсялiнiйно¨ |
порядку, можна ïредставиf-, |
||
20* |
ˆ |
ˆ |
307 |
f = aσˆx + bσˆy + cσˆz + dI. |
|||

Цей вираз актич о ¹ так званим амiльто а4.
стануЗнайдемо власнi ункцi¨ операторiвкватернiоном2. Äëÿ îñíовного |
||||||||||
|
|
|
|
|
|
|
|
|
ˆ |
ˆ |
|
|
|
|
|
|
|
|
|
Jz |
J |
|j, m = |1/2, 1/2i ма¹мо рiвняння |
|
|||||||||
У матричнiй ормi цей кетJ |
- |
|
2 |
, 2 E |
= 0. |
|
||||
|
|
+ |
|
1 |
1 |
|
|
|
||
|
|
|
ˆ âåêòîð |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
а рiвняння для нього: |
|
2 , |
2 E |
= β |
, |
|
||||
|
|
1 |
|
1 |
|
|
|
α |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ê |
|
|
1 |
|
= 0. |
|
|
|
|
0 |
α |
|
|
||
|
|
0 |
0 |
β |
|
||
Цеумовам:наомтричною4ïагавсяВидатнийривелолекснихзнайтиiнтерпретйогочиселлавнову1843дськацi¹ю,системуроцiйякматематикдодлявинайденняомплекзвичайосновнiВiльямíèõ êчиселомпватерноуанексзонiвтакоюамiльтонихчиселжчотинаоч(1805ичленнихплощинiою1865)гео-. |
|||||||
|
|
|
|
|
|
|
|
|
Êâàòåðíiîíè |
|
|
|
кватернiîíà, |
||
|
|
|
|
одиницi i, j, k |
ïiäê ðенi таким |
||
|
|
t + ix + jy + kz, |
|
|
|||
|
|
2 = j2 = k2 = −1, |
|
|
|
||
êâатернiон |
ij = k, |
|
ki = j, |
|
jk = i, |
|
|
ji = −k, |
|
t − |
|
−1(xσˆx + yσˆy + zσˆz ) |
|||
Величину |
|
|
ik = −j, |
kj = − . |
|
||
Легквòернiокторамiльтоназаíоюiв,уважитамiль.що.тонВi,кликщоалозвавосновнiйгозаймалинерозумiнняскалярноюшколадиницiвинятковiриличастин¹матрицямиспрâåîунтивюiверсальнесцеуматематичномуПалi,знаякiченняпомноженiiйсвiтiтеорi¨твор.- |
|||||||||||||||
наквачос |
t |
|
|
|
|
|
|
|
|
|
|
|
ix + jy + kz |
||
√ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− −1 |
|
|
√ |
|
|
|
√ |
|
|
|
|
|
√ |
|
|
Îòæå, |
|
= − |
|
, |
зобразити |
−1 σˆy , |
|
k = − |
|
|
|||||
308знача¹ться: |
−1 σˆx |
j = − |
|
|
−1 σˆz . |
|
|
||||||||
|
можна |
ÿê |
|
|
|
|
|
|
|
||||||
ìiñöå òà |
|
|
кватернiонiв у |
|
√ |
|
|
|
Öèì |
|
|||||
|
|
|
|
ðîëü |
|
|
|
|
математицi. |
. |
|
i âè- |
|||
Çâiäñè β = 0, а з умови нормування |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
нахточнiстюдио, |
ùî |
|
|
(α β ) |
|
|
|
α |
|
|
|
= α 2 + β |
2 = 1, |
|
|
|
|
|||||||||||||||||||||||||||||||
покладемо до |
|
|
|α| |
2 |
= 1 |
|
|
|
β |
|
|
|
| |
| |
|
|
|
| |
| |
|
|
|
|
|
|
|
||||||||||||||||||||||
ç |
|
|
|
|
|
азового.множниОскiльêиа, хвильовуто,незменшуючиункцiюзагальностi,визнача¹мо |
||||||||||||||||||||||||||||||||||||||||||
|
|
|
α = 1. Îòæå, |
|
|
|
|
|
|
|
|
|
|
|
ñòàí,= |
|
|
|
. |
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
óíêöiÿ îïè2ñó¹, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
2 |
|
0 |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
E |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
1 |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
Ця хвильова |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
у якому проекцiя спiну на вiсь |
||||||||||||||||||||||||
äîðiâíþ¹ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z |
||||||
|
|
~/2. Часто ¨¨ позначають скорочено як |
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
çíàõi ãîâîдиморять, |
хвильовущовонаопису¹ |
|
|
|
|
|
|
|
= |
1 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
ункцiю,станякаспiнопису¹уверхстан. Iз загально¨спiн униз ормули |
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ↑i |
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Îòæå,= |
|
|
, |
|
− |
|
|
E |
= |
|
|
|
|
|
|
|
, |
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
= |
|
. |
||||||||||||||
2 |
|
2 |
|
~ |
|
2 |
|
2 |
|
|
|
1 0 |
0 |
1 |
||||||||||||||||||||||||||||||||||
| ↓i |
1 |
|
|
1 |
|
|
|
|
Jˆ− |
|
1 |
|
|
1 |
|
|
E |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
0 |
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ↓i |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Знайдемо явнi вирази для операторiв повороту. Почнемо з |
|
|||||||||||||||||||||||||||||||||||||||||||||||
ˆz |
|
|
ˆ |
|
|
|
|
|
i ϕ2 σz |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
i J~z ϕ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Rϕ = |
e |
|
|
|
|
= e |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
ϕ |
|
|
|
+ |
iϕ |
|
|
|
2 |
|
1 |
|
|
σˆz2 + |
iϕ |
3 |
1 |
|
|
|
|
|
|
|||||||||||||||||||
= Iˆ |
+ i |
|
|
σˆz |
|
|
|
|
|
|
|
|
|
|
|
|
|
σˆz3 + · · · |
|
|
|
|||||||||||||||||||||||||||
2 |
|
2 |
|
|
|
|
2! |
2 |
|
3! |
|
|
|
|||||||||||||||||||||||||||||||||||
= Iˆ |
|
|
1 + 2! |
2 |
|
|
|
|
+ |
|
4! 2 |
|
|
|
|
+ · · ·! |
|
|
|
|
|
309 |
||||||||||||||||||||||||||
|
|
2 |
|
4 |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
1 |
|
|
iϕ |
|
|
|
|
|
|
1 |
|
|
|
iϕ |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+ |
σˆz |
|
iϕ |
|
+ |
iϕ |
|
3 1 |
+ · · ·! |
= Iˆcos |
|
ϕ |
+ iσˆz sin |
ϕ |
|
|
||||||||||||||
|
2 |
|
2 |
|
|
3! |
|
2 |
|
2 |
|
. |
||||||||||||||||||
Матриця= |
|
|
|
|
cos 2 |
|
+ |
|
|
|
|
|
i sin |
|
|
2 |
|
= |
ei ϕ2 |
|
i ϕ |
|||||||||
|
|
1 0 |
|
|
|
ϕ |
|
1 0 |
|
|
|
|
ϕ |
|
0 |
|
||||||||||||||
|
|
0 1 |
|
|
|
|
|
|
0 |
|
|
−1 |
|
|
|
|
|
|
|
|
0 e− 2 |
|
||||||||
|
ˆz |
ˆ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
Rϕ, ÿê i Jz |
, ¹ дiагональною. |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
Аналогiчно |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
àáî |
|
|
|
|
|
ˆy |
|
|
ˆ |
|
θ |
+ iσˆy sin |
θ |
, |
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
Rθ = I cos |
2 |
2 |
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Нарештi |
|
|
|
|
Rˆθ = |
|
|
|
2θ |
θ |
|
θ |
. |
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
y |
|
|
|
|
|
cos |
|
|
sin 2θ |
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
− sin 2 |
|
cos 2 |
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
ˆx |
|
|
ˆ |
α |
|
|
|
|
α |
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
Rα = I cos |
2 |
+ iσx sin |
2 |
|
, |
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
x |
|
|
|
|
|
cos α2 |
|
|
i sin α2 |
|
|
|
|
|
|
|
|
|
|
|
|
|||
розпадЯк iлюстрацiю застосуванняˆ |
знайдених виразiв розглянемо |
|||||||||||||||||||||||||||||
|
|
|
|
|
Rα |
= |
|
|
|
α |
|
|
α |
. |
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
i sin |
2 |
|
|
cos 2 |
|
|
|
|
|
|
|
|||||||||
утворенняпаду адронiвчастинокроçпадурахунок.Цейрозпадслабко¨¹ |
|
|
|
|
|
|
|
|
|
озглептонноголянемореакцi¨роз- |
||||||||||||||||||||
Λ0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
приклавза¹модi¨ом. бе |
|
|
|
|
||||||||||
|
|
|
|
|
|
Λ0-частинки т |
K0-мезона: |
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
π− + p → Λ0 + K0, |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
Λ0 → p + π−, |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
310 |
|
|
|
|
|
|
|
|
|
K0 → π+ + π−. |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
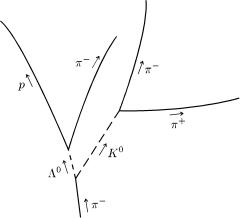
Стрiлкамицелiнi¨слiдиСхематичношляхзарядженихпозначенонейтральнихцiреакцi¨напрямкичастинокзображенiчастинокрухуу бучастинокльбашкнарис0 .овiй.36.якiСуцiльнiамерi,штриховi0-лiнi¨мезона.
ис. 36. Утворення i безлептонний розпад Λ -частинки та K
слiдiвПерша. реакцiя це народженняΛ0 ò K0, |
не залишають |
||||
мезонапротонi в вiдбуваютьсльбашковiй |
àìåði ç ðiä0 им воднем |
iä äi¹þ0-мезона |
|||
|
|
Λ -частинки т |
K |
|
|
. Вона ¹ прикладом |
сильних вза¹модiй. озпади |
π−- |
|||
|
|
|
|
Λ0- ò |
|
увагу0-частиннаОскiлькизпадi |
я завдяки слабкiй вз ¹ |
одi¨. Зосере |
èìî |
||
K |
|
|
|
|
|
Нехай ¨¨ спiн, який0-частинкиiвню¹системi центрà ìàñ (äèâ. ðèñ. 37). |
|||||
|
Λ |
|
|
|
|
îñi |
|
1безспiнова,/2 напрямлений уверх у довж |
|||
|
|
|
|
збере |
|
|
руху пiсля розпаду спiнтоiзпротона,закону рiвний |
||||
женняz. моменту кiлькостiпiончастинк |
|
|
|
||
1¹ìî,ãî/2розпадутакж дорiвню¹напрямлений увер . Нехай мплiтуда iмовiрностi так
т i спiнщоампротоналiудапiсляцьогорозпадупроцесубудедорiвню¹0-чнапрстинкиямле ийапрямленийуниз.Приймауниз,- a. ßêùî ñïií Λ
яка йм вiрнiс ь того, що протон вилетитьbпiд.Поставимокутом питання:
Äëÿ öüîго подi¹мо на хвильову ункцiю |
θ äî îñi z? |
|
Λ0-частинки |
|Λ0i = | ↑i |
311 |
