Глава 3. Симплекс-метод решения задачи линейного программирования

3.1. Идея симплекс-метода

Симплекс в - мерном пространстве – простейший многогранник.

гранник

–треугольник

– тетраедр

Так как оптимальное решение достигается в угловой точке области допустимых решений, то искать оптимальное решение нужно среди опорных решений. Сначала найти произвольное опорное решение. Это вершина многогранника решений. Вместе с соседними с ней вершинами она образует симплекс в пространстве свободных переменных. Перейти к соседней вершине симплекса с лучшим значением критерия, двигаясь по одному из ребер симплекса (лучше по ребру, более близкому к вектору градиента функции).

Этапы симплекс-метода:

1. Построение начального опорного плана .

2. Проверяется признак оптимальности решения.

3. Построение нового опорного решения – переход от одной вершины симплекса к другой .

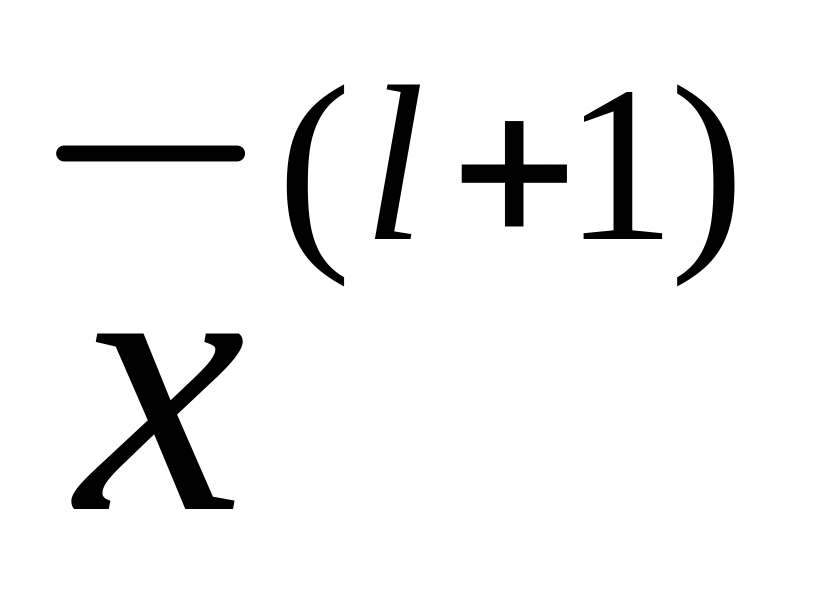4. l=l+1, повторять со второго пункта до тех пор, пока не выполнятся условия оптимальности.

3.2. Векторное представление симплексных преобразований

Пусть имеется опорный план и он невырожденный.

- базисная матрица.

- небазисная матрица.

Рассмотрим произвольное допустимое решение (это не угловая точка):

, подставим в условие (2).

(9)

Выразим базисные переменные через свободные и найдем общее решение системы уравнений:

(10)

Рассмотрим критерий на произвольном решении :

(13)

,

(11)

где

На опорном плане свободные переменные равны нулю, поэтому

(12)

(14)

,

а критерий в произвольной точке области выразится через свободные переменные в виде

Теорема 4: Опорный план задачи ЛП является оптимальным, если все оценки свободных переменных неотрицательны, т.е. .

Доказательство:

Для

т.к. , то и .

Значит решение оптимальное, так как во всех точках области значение критерия меньше ( ), чем критерий в точке .

Теорема доказана.

3.3. Симплекс-метод в уравнениях

Рассмотрим симплексные преобразования на конкретном примере

Приведенная математическая модель может быть моделью следующей экономической задачи:

Определить объемы производства двух видов продукции, обеспечивающий наибольший доход, если в производстве используется 3 типа ресурсов, запасы которых соответственно 160, 40, 200. Доход от единицы продукции 10 и 7 соответственно. Нормы расхода ресурсов заданы матрицей . Оставшийся неиспользованным второй ресурс можно реализовать по цене 2.

Обозначая объемы производства продукции , получим ограничения

Сначала найдем опорный план. Возьмем за базисные переменные , занулим свободные переменные, тогда опорный план будет .

Для анализа этого опорного плана получим общее решение:

Проанализируем опорный план на оптимальность:

Решение не оптимальное, так как увеличение приводит к увеличению критерия, и увеличение также увеличивает критерий.

Будем увеличивать переменную , т.е. вводим ее в список базисных переменных.

При росте x₁ уменьшаются базисные переменные x₃ и x₄. Определим, какая из них первая обратится в 0.

Первая обратится в 0 x₄ при θ =20.

Следующее опорное решение будет . Это и есть новая угловая точка.

Проверим ее на оптимальность. Для этого получим новое общее решение, взяв за базисные переменные . Переменную выразим из второго уравнения и исключим её из двух других уравнений и из критерия:

При росте все базисные переменные уменьшаются. Будем увеличивать до тех пор, пока одна из базисных переменных не обратится в ноль.

Минимальное значение из . Получим новое опорное решение .

Для анализа на оптимальность получим новое общее решение. Растущая переменная входит в список базисных, замещая переменную .

Увеличением улучшить критерий нельзя, любое их увеличение уменьшает критерий.

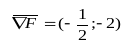
Значит, найденное нами решение является оптимальным. Значение критерия на этом решении равно 240.