§3.2. Основные законы радиоактивного распада

Радиоактивный распад – явление принципиально случайное. Нельзя предсказать, когда именно распадется данное радиоактивное ядро, а можно лишь указать с какой вероятностью оно распадется за тот или иной промежуток времени. Распад отдельного радиоактивного ядра не зависит от присутствия других ядер и может произойти в любой интервал времени. Наблюдения за очень большим числом одинаковых радиоактивных превращений ядер позволяет установить вполне определенные количественные закономерности для характеристики процесса радиоактивного распада.

Естественная статистическая величина, характеризующая радиоактивный распад, – постоянная (или константа) распада λ – определяет вероятность распада ядра в единицу времени и имеет размерность [время]^‑1. Экспериментальные и теоретические исследования позволяют заключить, что постоянная распада λ не зависит, по-видимому, от времени, прошедшего с момента образования радиоактивного ядра, что отражено в названии.

Пусть радиоактивное ядро достоверно существует в некоторый момент времени t = 0, условно принимаемый за ноль. У такого ядра к произвольно выбранному моменту времени t может реализоваться одна из двух возможностей:

1. ядро испытало радиоактивный распад и вероятность такого события равна ;

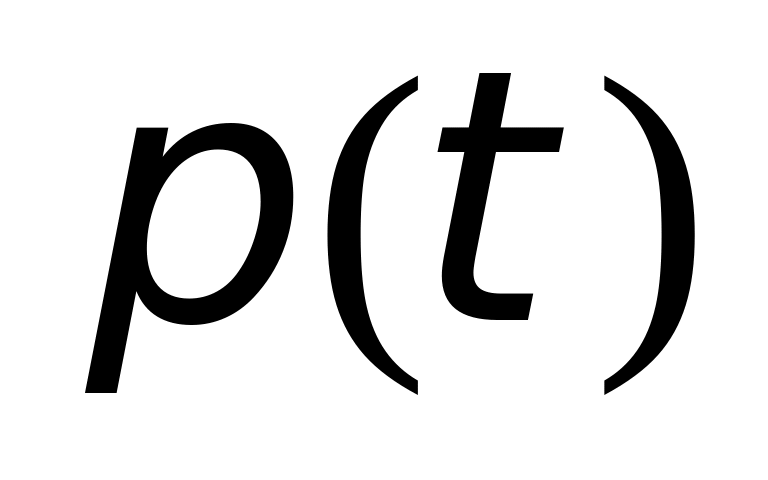2. ядро не испытало радиоактивного распада и вероятность такого события равна .

Очевидно, что

(3.2.1)

Установим, чему равна вероятность испытать ядру радиоактивный распад за интервал времени от t до (t+dt), т.е. предварительно не испытав распада за время . Вероятность такого сложного события

(3.2.2)

где λdt - вероятность распада ядра внутри временного интервала dt (постоянная распада λ не зависит от времени!). Используя (3.2.1) уравнение (3.2.2) приведем к виду

.

(3.2.3)

Поскольку ядро достоверно существует в момент времени , то имеем очевидное начальное условие . Тогда искомая вероятность составит

(3.2.4)

При помощи (3.2.1) и (3.2.4) найдем для ядра вероятность q(t) не испытать распада к моменту времени t:

(3.2.5)

Соотношения (3.2.4) и (3.2.5) содержат полное описание статистических свойств радиоактивного распада ядер и позволяют определить любые статистические характеристики распада.

Найдем среднее время жизни ядра, используя определение для математического среднего:

(3.2.6)

поскольку – вероятность того, что ядро, прожив время t, распадется за время между .

Пусть в момент времени t = 0 имелось N₀ радиоактивных ядер одной природы. Наиболее вероятное (ожидаемое) число ядер N(t), которые не испытают радиоактивного распада к моменту времени t, должно составить

,

(3.2.7)

а соответственно число распавшихся ядер (d – decay – распад)

(3.2.8)

Формула (3.2.7) выражает основной закон радиоактивного распада. Следует еще раз подчеркнуть, что имеют смысл наиболее вероятного количества оставшихся и распавшихся радиоактивных ядер к моменту времени t. Реальные же количества радиоактивных ядер к моменту времени t могут быть как больше , так и меньше. Используемая далее в выражениях величина N, если не оговорено иное, всегда имеет смысл среднего числа ядер.

В ядерной физике и ее приложениях используется еще одна временная характеристика распада – период полураспада Т_1/2, которая определяет время, за которое первоначальное количество ядер N₀ должно уменьшиться в два раза. Установим связь между периодом полураспада Т_1/2 и постоянной распада λ. По определению

(3.2.9)

откуда

(3.2.10)

Сравнивая это выражение с (3.2.6) устанавливаем, что

(3.2.11)

Для характеристики радиоактивных свойств вещества, т.е. совокупности большого числа радиоактивных ядер, служит специальная величина, характеризующая скорость радиоактивных превращений, которая называется активностью. Активность А (не путать с массовым числом А!) – среднее число ядер в образце, испытавших радиоактивный распад за единицу времени. Для радиоактивных ядер одной природы получим, используя (3.2.8):

(3.2.11)

Полученное выражение можно записать в следующем виде (учитывая (3.2.7)):

(3.2.12)

или же в виде

(3.2.13)

где - начальная активность образца.

Единицей измерения активности в СИ служит беккерель (Бк),

1 Бк = 1 распад/с.

Часто в практических приложениях используется другая единица измерения активности - кюри (Ки):

1 Ки = 3,7·1010 Бк.

Активность, отнесенная к массе радиоактивного препарата, называется массовой удельной активностью. Для жидких и газообразных веществ иногда используют объемную удельную активность.

Для характеристики радиоактивных свойств нуклида одной природы (без учета вторичных компонент, возникающих после распада) используют удельную активность нуклида – активность единицы массы этого нуклида:

,

(3.2.14)

т.е. удельная активность нуклида не зависит от времени.

Для определения  (а, следовательно,  и Т_1/2) можно использовать формулу (3.2.12), если в некоторый произвольный момент времени измерить активность препарата и число радиоактивных ядер. Этим методом удобно пользоваться, когда период полураспада достаточно велик, и поэтому изменением числа радиоактивных ядер за время измерения активности можно пренебречь. Если период полураспада Т_1/2 не очень велик, то можно непосредственно снять кривую изменения активности через определенные интервалы времени. Затем по полученным значениям строят график зависимости натурального логарифма активности от времени. Постоянную распада  удобно находить, если записать (3.2.13) в виде:

(3.2.15)

З ависимость (3.2.15) представляет собой прямую, а  определяется по тангенсу угла наклона этой прямой (рис. 3.2.1) или непосредственно по уменьшению активности вдвое. В реальных условиях экспериментальные точки имеют неизбежный разброс, определяемый статистической природой процесса радиоактивного распада. Для проведения через такие точки наиболее достоверной прямой обычно используют метод наименьших квадратов, в результате чего среднеквадратичное отклонение точек от найденной прямой будет минимальным.

Весьма распространенными являются случаи распада радиоактивных ядер с образованием не только стабильных, но и радиоактивных дочерних ядер. В последнем случае возникают цепочки распадов. Примером таких цепочек могут служить рассмотренные выше радиоактивные семейства. Баланс числа радиоактивных ядер при этом определяется следующими уравнениями:

	(3.2.16)
. . . . . . . . . . . . .

где индекс 1 относится к первичным материнским ядрам, а индексы 2, 3, . . . – к дочерним. Распад ядер N₁ описывается обычным законом распада (3.2.7). Баланс ядер каждого дочернего вещества определяется скоростью собственного распада (активностью) и скоростью рождения, равной скорости распада ядер-предшественников. Решение каждого уравнения (3.2.16) зависит только от вида решения предшествующего. В простейшем случае, когда в начальный момент времени дочерних ядер нет, а количество материнских ядер равно N₁₀, решение каждого k-го уравнения из (3.2.16) имеет вид:

(3.2.17)

Полное число радиоактивных ядер есть сумма всех количеств ядер N_k, существующих в данный момент времени.

Из общего решения (3.2.17) получаем решение для N₂(t):

(3.2.18)

Из (3.2.18) следует, что в момент времени

,

(3.2.19)

количество ядер N₂ достигает своей максимальной величины

,

(3.2.20)

а затем монотонно убывает. Если ₁ << ₂ (или (Т_1/2 )₁  >> (Т_1/2 )₂) и t » (Т_1/2 )₂, то из (3.2.18) в пределе t → ∞ получаем

,

(3.2.21)

т.е. устанавливается динамическое равновесие между активностью материнского и дочернего препаратов, которое называется вековым равновесием. Вековое равновесие широко используется для определения периодов полураспада долгоживущих материнских нуклидов по известным значениям ₂ и отношению N₂/ N₁. Очевидно, что при выполнении соответствующих условий вековое равновесие может наступать для любой пары соседних элементов в цепочке распадов.

Другой предельный случай ₁ >> ₂ (или (Т_1/2 )₁  << (Т_1/2 )₂) при t » (Т_1/2 )₁ дает зависимость

,

(3.2.22)

которая фактически является кривой распада дочернего вещества.