21.Нелинейные электрические цепи при постоянном токе.

Если в цепи есть хотя бы 1 нелинейный эл-нт она нелинейная. Нелинейные цепи описываются нелинейными ур-ниями, которые составляются по з-нам Кирхгофа(з-н Ома в нелин цепях не работает). В общем случае эти ур-ния дифференциальные, но для частного случая – цепи постоянного тока, они алгебраически нелинейны.

Для аналитического решения нелинейных ур-ний нет регулярных методов, поэтому пользуются графическими или численными методами. В начале необходимо знать зависимости напряжения от тока на всех нелинейных эл-тах цепи( ВАХ или АВХ).

22.Нелинейные элементы и их характеристики.

Нелинейные эл-ты подразделяются на резистивные, индуктивные и емкостные.

Для линейного эл-та R=u/i=k*tg, где  - угол наклона ВАХ.

Для нелинейных элементов ВАХ разделяются на статические и динамические: Статические получаются при мелденном изменении напряжения и тока, динамические – при быстром. Как правило по форме они отличаются.

{R=Ro(1+t)}

Но в некоторых случаях статическую хар-ку можно использовать вместо динамической, т.е. существуют статические сопротивления и проводимости, и динамические сопротивления и проводимости.

Для каждой точки нелинейных зависимостей своё значение R и G. Rст=k*tg. Gст=1/Rст. З-н Ома применим только для конкретной точки, а не для всей прямой.

] статическая и динамическая хар-ки совпадают, в этом случае Rдин в заданной точке равняется производной напряжения по току: Rдин=lim(0)[u/i]=du/di=k*tg.

Rст и G ст – явл-ся ф-циями тока, они всегда положительные, если цепь не содержит источников энергии. Rд и Gд положительные для точек лежащих на восходящей части кривой и отрицательные для точек на низходящей.

23.Расчёт простых цепей постоянного тока с пассивными нелинейными элементами (графический метод).

Основные методы рассчёта нелин эл цепей: 1)графический, 2)аналитический, 3)численные методы.

] ВАХ нелинейных эл-тов нам известны и описываются ф-циями u/1/=F/1/(i/1/) и u/2/=F/2/(i/2/).

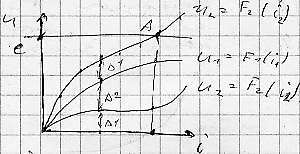
i/1/=i/2/=i, e=u/1/ + u/2/.

Т.к. ток проходящий по цепи один и тот же, а вел-на эдс = сумме напряжений на нелинейных элементах, то складываем ординаты хар-к u/1/ и u/2/; получаем новую хар-ку u=F(i). Из точки А находим искомую хар-ку (i, u1, u2).

Данный алгоритм позволяет рассчитывать цепочки из любого кол-ва последовательно соединённых лин и нелин эл-тов.

При параллельном соединении эл-тов производится суммирование абсцисс.

24.Расчёт простых цепей постоянного тока с пассивными нелинейными элементами итерационным методом.

Для расчётов цепей с нелинейными эл-тами часто применяют итерационный метод решения нелинейных алгебраических ур-ний.

Метод итерации заключается в выборе начальных значений напряжений или тока на НЭ-те, составлении ур-ний цепи по з-нам Кирхгофа, подставлении в эти ур-ния начальных значений I и U, решение этих ур-ний, с последующим уточнением начальных значений U и I; подставлением этих уточнённых значений в ур-ния цепи, решение этих ур-ний, очередное уточнение значений напряжения и тока и т.д.

Первая схема расчёта (по напряжению). Используется ур-ние цепи U=E-Rв*I=F(U). Алгоритм: 1)сначала задаёмся начальными значениями напряжения Uo, по кривой 2 находим соответствующий ток на нелинейном эл-те UoIo; 2)Io подставляем в ур-ние U=E-Rв*I=F(U). Решаем это ур-ние и находим уточнённое значение U/1/. 3)по кривой 2 находим соответствующее U/1/ значение тока I/1/. 4)Уточнённое значение тока I/1/ подставим в ур-ние, решаем и находим U/2/ и т.д.

Не для всех точек кривой 2 данная схема даёт сходящееся решение. Для точки «b» схема неприменима, т.к. решение расходится. Применимость расчётной модели определяется по критерию сходимости |dF(u)/dU|<1.

Для точек типа «b» применяется расчётная схема по току.