12.Однородная линия при различных режимах работы.

z – полное комплексное сопротивление. Z – модуль z, т.е. z=Z*e^(j). Для придания универсальности решению начало координат поместим в конец линии, т.е. в предыдущих формулах х заменим на l-x (l- длина линии).

U\.\=A/1/*e^[(l-z)] + A/2/*e^[(l-x)] = A/1/*e^(-l)*e^(x) + A/2/*e^(l)*e^(-x);

z*I\.\=A/1/*e^[-(l-x)] – A/2/*e^[(l-x)] = A/1/*e^[-l]*e^(x) – A/2/*e^(l)*e^(-x).

U\.\=A/3/*e^(x)+A/4/*e^(-x);

z*I\.\=A/3/*e^(x) – A/4/*e^(-x).

А/3/, А/4/ находим рассматривая эти ур-ния для конца линии (х=0).

U\.\/2/=A/3/+A/4/; zI\.\/2/=A/3/ - A/4/. A/3/=½(U\.\/2/+I\.\/2/*z); A/4/=½(U\.\/2/ - I\.\/2/*z).

{U\.\=½(U\.\/2/+I\.\/2/*z)*e^(x) + ½(U\.\/2/ - I\.\/2/*z)*e^(-x); (*)

{zI\.\=½(U\.\/2/+I\.\/2/*z)*e^(x) – ½(U\.\/2/ - I\.\/2/*z)*e^(-x). – рабочие ур-ния линии в показательной форме. Представим эти ур-ния в геометрической форме:

[U\.\=U\.\/2/*chx +I\.\/2/*z*shx; [I\.\=I\.\/2/*chx + (U\.\/2/)/z*shx.

Режимы работы: 1)Режим х.х. zпр=, I\.\/2/=0.

U\.\/o/=U\.\/2o/*chx; I\.\/o/=(U\.\/2o/)/z*shx. z/o/= (U\.\/o/)/(I\.\/o/) = z*cthx.

Из этого ур-ния видно, что если длина линии меньше ¼ длины волны, то действующее значение тока к концу линии убывает, а действующее значение напряжения возрастает.

2)Режим к.з. U\.\/2/=0, zпр=0.

U\.\/k/=I\.\/2k/*z*shx; I\.\/k/=I\.\/2k/*chx, z/k/=zthx.

Т.к. режимы х.х. и к.з. известны, отдельно эксплуатационный режим можно не рассматривать, т.к. по известным z/o/ и z/k/ можно вычислить параметры линии в любом рабочем режиме, напр волновое сопротивление z=[z/o/*z/к/], thl=[(z/k/)/(z/o/)].

Любой режим можно представить наложением режимов х.х. и к.з. для этой линии. В этом случае напряжение в любой точке линии может определяться по формуле: U\.\=U\.\/2/[chx+z/zпр*shx) = U\.\*[ch(l+)]/ch; =th(z/zпр). По аналогии ток в любой точке линии: I\.\=I\.\/2/*[chx+zпр/z*shx] = I\.\/2/*[sh(l+)]/sh, =cth[z/zпр].

13.Режимы работы линии без потерь.

При высоких частотах, когда ёмкостная проводимость много больше омической, индуктивное сопротивление много больше омического сопротивления, т.е. С>>G, L>>R, линию можно представить, как линию без потерь.

=0, =j, фазовая скорость U=C, Коэффициент фазы =LC, волновое сопротивление линии z=(L/C).

Рассчит режим х.х. I\.\/1/=0, U\.\/o/=U\.\/2o/*chx=<{с учётом =j получим}>=U\.\/2o/*cosx; I\.\/o/=(U\.\/2o/)/z*shx =+j*(U\.\/2o/)/z*sinx= <{т.к. в этом случае полное комплексное сопротивление равно модулю, то}>=+j*(U\.\/2o/)/Z*sinx. Определим входное сопротивление линии: z/o/= - jZ*ctgx=j*Xl.

Построим зависимости для тока, напряжения и сопротивления:

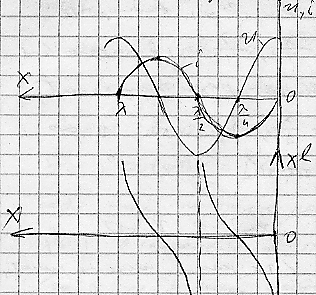
Промежутки 0-/4 (X/l/<0) – линия имеет емкостной хар-р, в промежутке /4-/2 (X/l/>0 – линия имеет индуктивный характер.

Из графиков для u и i видно, что в точках x=/4; 3/4 и т.д. сопротивление линии z/o/=0, имеет резонанс напряжений. В точках x=/2,  и т.д. z/o/=, имеет резонанс токов.

Режим к.з. x/пр/=0, U\.\/2/=0.

U\.\/k/=I\.\/2k/*z/k/*shx= <т.к. рассм неискаж линия, =j, то> = I\.\/2k/*Z*j*sinx.

I\.\/k/=I\.\/2k/*chx=I\.\/2k/*cosx (cos – чётная ф-ция и на j не умножается). z/к/=(U\.\/k/)/(I\.\/1k/) = Z*j*tgx.

И в случае к.з. образовываются стоячие волны.

Для x=/2 и  имеем узлы напряжения и пучности тока. При x=/4, 3/4 имеем узлы тока и пучности напряжения. Следовательно, для 2-го случая (/4, 3/4) z/к/= - резонанс токов; в 1-м случае (/2, ) z/к/=0 – резонанс напряжений. z/к/=j*Z*tgx=j*Xl => линия ведёт себя, как некоторое реактивное сопротивление Xl; в интервале от 0 до /4 Xl>0 и ведёт себя как индуктивность, в интервале от /4 до /2 Xl<0 и линия ведёт себя, как ёмкость => длиной линии можно выбирать характер линии. Для линии длиной /4 наблюдается резонанс токов, линия обладает малым затуханием и  большим сопротивлением. Поэтому такие линии можно использовать в качестве изоляторов. Обычно это делается при высоких частотах.

Режим реактивной нагрузки. zпр=jXпр. U\.\=U\.\/2/(chx+z/zпр*shx)=U\.\/2/*(cosx+z/Xпр*sinx) = U\.\/2/*[sin(x+)]/sin.

 - характеризует соотношение между сопротивлением приёмника и линии: tg=Xпр/Z.

По аналогии из 2-го ур-ния получаем: I\.\=I\.\/2/*[cos(x+)]/cos. Из этих выражений видно, что и в случае реактивной нагрузки получаются стоячие волны, но графики будут сдвинуты влево на вел-ну /.

z/x/=(U\.\)/(I\.\)=[U\.\/2/*sin(x+)/sin]/[I\.\/2/*cos(x+)/cos] = j*Xпр*[tg(x+)]/tg.

Сопротивление линии изменяется по закону tg, но в конце линии u и i нет ни пучности ни нуля, т.к. график сдвинут на вел-ну /.

Случаи: 1)Xпр=Zctgl (это условие выполняется когда =/2 - l). z/x/=(имеем резонанс токов).

2)Xпр= - Z*tgl, = - l, тогда сопротивление линии =0.

Заключение: Во всех 3-х режимах появляются стоячие волны, пучности и узлы которые находятся на расстоянии /4. Никакого переноса энергии в случае стоячих волн нет. Приёмник энергии не потребляет, поэтому необходимо иметь не стоячие, а бегучие волны.

14.Расчёт классическим методом переходного процесса в однородной неискажающей линии.

Как и в случае уст-ся режимов ур-ния записываются в частных производных:

- U/x=R*i+L*di/dt, - i/x=GU+C*dU/dt. R/L=G/C= (1).

Введём новые переменные: u=u/1/*e^(-t); i=i/1/*e^(-t);

U/x=(u/1/)/x*e^(-t); U/t=(u/1/)/t*e^(-t)+u/1/(-)*e^(-t). i/x=(i/1/)/x*e^(-t), i/t=(i/1/)/t*e^(-t)+i/1/(-)*e^(-t).

Подставим получившееся в ур-ние (1) и разделим получившееся ур-ние на e^(-t): - (u/1/)/x=Ri/1/+L/1/*(i/1/)/t+i/1/(-), <{ Ri/1/ и i/1/(-) сокращаются}>. По аналогии -(i/1/)/x=C*(u/1/)/t. Первое ур-ние дифференцируем по х, второе – по t: -(²u/1/)/x²=L(i/1/)/(xt); - (i/1/)/(xt)=C(²u/2/)/t². Подставим 2-ое ур-ние в 1-ое: (²u/1/)/x²=LC(²u/1/)/t².

Фазовая скорость =1/[LC]. (²u/1/)/x²=1/p²*(²u/1/)/t².; (²u/1/)/t²=²*(²u/1/)/x².(*).

=x-t; =x+t. Найдём производные  и  по x и по t:

/x=1; /x=1; /t=0; /t=0;

(u/1/)/x=(u/1/)/ + (u/1/)/; (u/1/)/t= - (u/1/)/ + (u/1/)/;

(²u/1/)/x²=(²u/1/)/² + 2(²u/1/)/ + (²u/1/)/²; (²u/1/)/t²=²(²u/1/)/² - 2(²u/1/)/ + ²(²u/1/)/².

Эти ф-лы подставим в ур-ние (*). Подставим в волновое ур-ние следующее условие: (²u/1/)/=0=/*[(u/1/)/]=0; (u/1/)/=() и проинтегрируем u/1/=()d + () = () + (). Возвратимся к переменным x и t и запишем общее решение уравнения: u/1/=(x - t) + (x +t) (2). u=[(x - t) + (x + t)]*e^(-t). Найдём ток i/1/ для этого в ур-ние: -(i/1/)/x=C(u/1/)/t подставим ур-ние (2):

- (i/1/)/x = C[[() + ()]]/t = C[/*/t + /*/t] = C*[- / + /] = <{/x=/; /x=/}> = - [C/L]*[/x - /x].

i/1/=[C/L]*[(x - t) - (x - t) + f(t)].

i=[C/L]*[(x - t) - (x - t)]*e^(-t).

Введём новую величину, характеризующую затухание сигнала в линии, которая наз-ся коэффициентом затухания неискажающей линии: =[RG].

u=(x - t)*e^(-x) + (x + t)*e^(x). i=[C/L]*[(x - t)*e^(-x) - (x + t)*e^(x)].

Ф-ции  и  отличаются от ф-ций  и  в предыдущих выражениях на величину e^[(x-t)], e^[(x-t)]. Получим общий вид решения волнового ур-ния. Выбор ф-ции  и  зависит от условий задачи.

15.Расчёт операторным методом переходного процесса в однородной неискажающей линии.

Поскольку в однородной линии ток и напряжение являются функциями 2-х переменных i=f(x,t), u=f(x,t), можно ввести их операторное изображение:

u(t,x).=’U(p,x)=(0)u(t,x)e^(-pt)dt.

i(t,x).=’I(p,x)=(0)i(t,x)e^(-pt)dt.

u/t.=’pU(p,x) – u(o,x), t=0, u/x.=’d/dx*U(p,x);

i/t.=’pI(p,x) – i(o,x), i/x.=’d/dx*I(p,x).

-(dU(p,x))/dx=R*I(p,x) + pLI(p,x) – L*i(o,x),

-(dI(p,x))/dx=GU(p,x) + pCU(p,x) – C*u(o,x).

Полученная система ур-ний состоит из обыкновенных дифф ур-ний по переменной х.

Граничные условия явл-ся ф-цией по ординате. Зададим граничные условия x=0, x=l и начальные условия i(o,x)=0, u(o,x)=0. В этом случае выражение имеет следующий вид:

-(dU(p,x))/dx=(R+pL)*I(p,x); -(dI(p,x))/dx=(G+pC)*U(p,x).

Введём коэффициент =[(R+pL)(G+pC)]. После этого продифференцируем ур-ние (1) по х с учётом (2)-го: d²U(p,x)/dx²=²*U(p,x). Решение полученного ур-ния ищется в виде U(p,x)=A/1/*e^(-x) + A/2/*e^(x).

A/1/=F/1/(p), A/2/=F/2/(p).

I(p,x)=1/Z(p)*[(A/1/)*e^(-x) – (A/2/)*e^(x)].

Z(p)=[(R+pL)/(G+pC)], Z(p) – операторное волновое сопротивление линии.  - операторный коэффициент распределения. Для неискажающей линии R/L=G/C.

Z(p)=[L/C], =[RG]+p[LC]=+p/U.

Подставляем Z(p) в выражения и получаем:

U(p,x)=[F/1/(p)*e^(-px/U)]*e^(-x) + [F/2/(p)*e^(px/U)]*e^(x).

I(p,x)=[C/L]*[(F/1/(p)*e^(-px/U))*e^(-x) – (F/2/(p)*e^(px/U))*e^(x)]. Перейдём к оригиналу с использованием линии: u(t,x)=(x-Ut)*e^(-x) + (x+Ut)*e^(x), i(t,x)=[C/L]*[(x-Ut)*e^(-x) - (x+Ut)*e^(x)].

(x-Ut) – представляет собой прямую волну напряжения и тока движущиеся со скоростью U от начала линии к её концу. (x+Ut) – представляет собой обратную волну напряжения и тока движущуюся со скоростью U.

В любой точке линии отношение между напряжением и током для прямой волны =[L/C], обратной волны = - [L/C].

Множитель e^(x) [e^(-x)] характеризует затухание волны. Причина затухания – превращение энергии эл-магнитных полей в теплоту.

16.Преломление и отражение волн в месте сопряжения двух однородных линий.

] волна /1/ доходит до места стыка 2-х однородных линий характеризующихся волновыми сопротивлениями Z/1/ и Z/2/. При выводе формул индекс 1 будет соответствовать 1-й линии, а индекс 2 – второй линии. ] для второй линии справедливо начальное условие: до подхода волны /1/ в ней не было тока и напряжения. При прохождении волной /1/ места стыка эта волна начинает распространяться по 2-ой линии не меняя своего направления. Эта волна наз-ся преломленной. Обозначим её /2/. Если линии не согласованы часть волны /1/ отражается от стыка и начинает распространяться по первой линии в обратную сторону. Линии наз-ся согласованными если Z/1/=Z/2/.

Отражённая волна идущая в обратную сторону по линии 1 обозначается /1/. Если Z/1/=Z/2/ отражённой волны не возникает. Прямая отражённая и преломлённая волны в месте стыка 2-х линий связаны друг с другом следующими соотношениями: u/1/=u//1// + u//1// = u//2// = u/2/, i/1/=[u//1// - u//1//]/(Z/1/) = (u//2//)/(Z/2/) = i/2/.

u//2//=[2Z/2/]/(Z/1/+Z/2/)*u//1//, i//2//=[2Z/1/]/(Z/1/+Z/2/)*i//1//. u//1//=[Z/2/ - Z/1/]/[Z/1/+Z/2/]*u//1//, i//1//=[Z/1/ - Z/2/]/[Z/1/+Z/2/]*i//1//.

Из полученных соотношений следует, что преломленные и отражённые волны имеют такую же форму, что и падающие. Величины (u//2//)/(u//1//); (i//2//)/(i//1//) – наз-ся коэффициентами преломления.

Величины (u//1//)/(u//1//)=q/n/; (i//1//)/(i//1//)=q/i/ - наз-ся коэффициентами отражения.

Преломленные и падающие волны совпадают по знаку. Знак отражённой волны зависит от соотношения Z/1/ и Z/2/. Если Z/2/>Z/1/ волна напряжения отражается без перемены знака, волна тока с переменой знака. Падающие волны тока в первой линии уменьшаются, а напряжение возрастает не более чем в 2 раза.

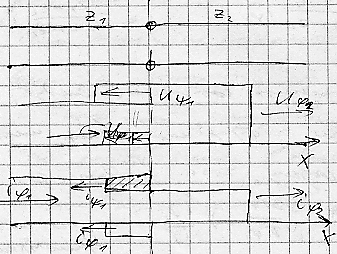
u//2//=u//1//+u//1//.

Даже если z/2/>>z/1/ преломленная волна напряжения не может превышать падающую волну более чем в 2 раза.

Если Z/1/>Z/2/ преломленная волна напряжения меньше падающей, а преломленная волна тока больше падающей. Волна напряжения меняет знак, а волна тока нет. В результате этого ток возрастает, но не более чем в 2 раза.

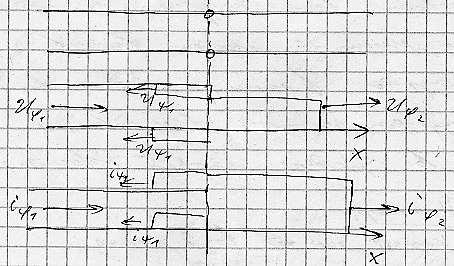
<) баланс мощностей в месте стыка 2-х однородных линий.

p=i/1/*u/1/=i/2/*u/2/.

(u//1// + u//1//)*[u//1// - u//1//]/Z = (u//1//²)/(Z/1/) – (u//1//²)/(Z/1/) = (u//2//²)/(Z/2/).

(u//1//²)/(Z/1/) = (u//1//²)/(Z/1/) + (u//2//²)/(Z/2/); P//1//=P//1//+P//2//. Если волна напряжения переходит из линии с малым сопротивлением в линию с большим волновым сопротивлением напряжение увеличивается и в пределе может удвоиться.

Волны могут вызвать значительное перенапряжение между соседними точками цепи, эти перенапряжения тем больше, чем круче фронт волны.