зависимых векторов определяется так же, как в случае с арифметическими векторами. При этом координатами вектора в базисе называют коэффициенты его разложения по базису. Линейная независимость векторов базиса обеспечивает единственность разложения по базису. Разложить вектор по базису означает найти его координаты в данном базисе.

Упражнения. Разложить:

a)медиану треугольника через вектора, соответствующие боковым сторонам. Ответ: (1/2, –1/2);

b)вектор DE , где E – середина BC; D – середина AS; тетраэдра SABC по боковым векторам. Ответ: (–1/2, 1/2, 1/2);

При решении задач обычно в качестве базисных на плоскости рассмат-

ривают i и j – векторы, по модулю равные единице и направленные по координатным осям Ox и Oy прямоугольной декартовой системы координат. Тогда записи a (x, y) и a = xi + y j эквивалентны. В трехмерном случае рас-

сматриваются базисные векторы i , j , k , а записи a (x, y, z) и a = xi + y j + zk равнозначны.

6.1. Скалярное произведение

Скалярным произведением двух векторов называют произведение их модулей на косинус угла между ними, т. е. a b = a b cos (a,b). Обозначаться

скалярное произведение может: ab или a b .

Свойства скалярного произведения.

Геометрические свойства:

1)a b a b = 0 (примечание: нулевой вектор перпендикулярен и параллелен любому вектору);

2)(a ,b ) – острый a b > 0; ( a ,b ) – тупой a b < 0.

Наглядным примером служит работа силы, которая может быть как положительна, так и отрицательна, в некоторых случаях равна 0. Результат обучения – «скалярное произведение усилий и способностей».

Алгебраические свойства:

1) a b = b a ; 2) (αa ) b = α(a b ); 3) ( a b ) с=( a c )+(b c ).

Вычисление скалярного произведения в координатах. Пусть есть произвольный базис i, j, k и два вектора, разложенные по этому базису. То-

23

гда скалярное произведение равно (x1i + y1 j + z1k)(x2i + y2 j + z2 k) . Раскрыв

скобки, получим сумму 9 слагаемых.

Но гораздо удобнее вычислять скалярное произведение в ортонормиро-

Применение скалярного произведения. Основным применением скалярного произведения является вычисление углов (разумеется, для ненулевых

(a, b) = arccos aa bb .

Упражнения:

1.Даны точки А (–1, –2, 4), В (–4, –2, 0), С (3, –2, 1). Найдите углы тре-

угольника АВС. Ответ: А = π2 , В = С = π4 .

2.Даны точки А (2, 2) и В (5, –2). На оси Ох найти точку М, такую, что угол АМВ прямой. Первый способ: составить уравнение окружности с диаметром АВ. Второй способ: обозначить координаты точки М за (x, 0) и составить уравнение. Ответ: (1, 0), (6, 0).

6.2. Нахождение площадей и векторное произведение векторов

Векторным произведением векторов a и b называется третий вектор a ×b , если верны следующие условия:

1)a ×b = a b sin (a, b) ;

2)a ×b a и a × b b ;

3)a , b , a ×b образуют правую тройку, т. е. изнутри угла, образованного

этими векторами, видно поворот от a к b и от b к a ×b против часовой стрелки.

24

динаты вектора a ; (xb, yb, zb)– координаты вектора b .

Эту формулу можно вывести из векторного произведения элементов ортонормированного базиса i, j, k .

Свойства векторного произведения:

1) a ×b = −b ×a . Векторное произведение векторов не коммутативно, т. е. нельзя переставлять сомножители векторного произведения;

2)(λa)×b =λ(a ×b);

3)(a +b)×c = a ×c +b ×c .

Применение векторного произведения. Основным применением век-

торного произведения является вычисление площадей фигур. Исходя из определения a ×b = a b sin (a, b) , площадь параллелограмма, построенно-

го на векторах a и b , как на сторонах, вычисляется по формуле S = a ×b . Пример. Для нахождения площади треугольника с вершинами в точках

= 7i + 23 j +11k .

Модуль этого векторного произведения a ×b = 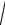72 + 232 +112 = 1777

есть площадь параллелограмма, а искомая площадь треугольника 12 1777 .

Произвольную сложную плоскую фигуру можно разбить на треугольники, а площадь произвольной фигуры есть сумма площадей треугольников.

25

6.3. Смешанное произведение

Смешанным произведением трех векторов a , b и с называется число, равное скалярному произведению вектора a ×b на вектор с, т. е. (a ×b , с).

Обозначаться смешанное произведение может: a b с или a b с. Рассматривая векторные произведения элементов ортонормированного

базиса i, j, k , можно вывести формулу для вычисления смешанного произве-

(xb, yb, zb)– координаты вектора b; (xc, yc, zc ) – координаты вектора с.

Свойства смешанного произведения:

1) смешанное произведение векторов не коммутативно в общем случае: a b с = с a b =b с a = – b a с = – с b a = – a с b;

2)смешанное произведение трех векторов равно нулю тогда и только тогда, когда векторы компланарны, т. е. лежат в одной плоскости;

3)смешанное произведение трех векторов равно объему параллелепипеда с ребрами, соответствующими этим векторам, если тройка правая, и объему со знаком минус, если тройка левая.

Применение смешанного произведения. Основным применением смешанного произведения является вычисление объемов фигур, так как из определения следует, что оно связано с объемом параллелепипеда и тетраэдра (объем тетраэдра в шесть раз меньше объема параллелепипеда).

7.УРАВНЕНИЯ ПРЯМОЙ И ПЛОСКОСТИ

7.1. Уравнение плоскости в пространстве

Выведем общее уравнение плоскости Ax + By + Cz + D = 0 в пространстве на следующем примере.

Пусть плоскость α, равноудаленная от точек X (1, 1, 1) и Y (3, 5, 9). Тогда каждая точка плоскости равноудалена от точек. Запишем это условие в виде

(x −1)2 + (y −1)2 + (z −1)2 = (x −3)2 + (y −5)2 + (z −9)2 . Возведя в квад-

рат, упростив, получим линейное выражение вида Ax + By + Cz + D = 0. Другой способ. Середина отрезка – точка M (2, 3, 5) – лежит в плоско-

сти, каждая точка которой равноудалена от точек X и Y, поэтому вектор (2, 4,

26