17 Общее уравнение плоскости в пространстве

Всякое уравнение вида  , где A, B, C и D – некоторые действительные числа, причем А, В и C одновременно не равны нулю, определяет плоскость в заданной прямоугольной системе координат Oxyz в трехмерном пространстве, и всякая плоскость в прямоугольной системе координат Oxyz в трехмерном пространстве определяется уравнением вида   при некотором наборе чисел A, B, C и D.

Нормальный вектор

Нормальный вектор плоскости - это любой ненулевой вектор, лежащий на прямой перпендикулярной к данной плоскости.

Полное и неполное уравнение плоскости.

Ax + By + Cz + D = 0 - полное уравнение плоскости (А,В,С) - вектор нормали к плоскости.

Если хотя бы один из коэффициентов равен нулю, уравнение не полное. Рассмотрим все виды неполных уравнений.

Геометрический смысл неполных уравнений

1. D=0 плоскость, проходящая через начало координат

2. А=0 плоскость параллельная оси 0х

3. В=0 плоскость параллельная оси 0у

4. С=0 плоскость параллельная оси 0z

5. А=0 В=0 плоскость параллельная плоскости 0ху

6. А=0 С=0 плоскость параллельная плоскости 0xz

7. В=0 С=0 плоскость параллельная плоскости 0yz

8. А=0 В=0 D=0 уравнение Cz=0 определяет плоскость 0ху

9. А=0 С=0 D=0 уравнение Ву=0 определяет плоскость 0xz

10. В=0 С=0 D=0 уравнение Ах=0 определяет плоскость 0yz

Уравнение плоскости, проходящей через заданную точку перпендикулярно вектору нормали

Пусть плоскость проходит через точку M₀ (x₀, y₀, z₀) и перпендикулярна вектору  (M, N, L). Вектор  (M, N, L) называется вектором нормали к плоскости.

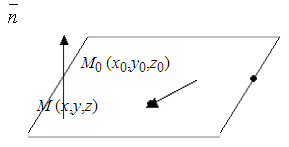
Возьмем произвольную точку M(x, y, z), лежащую в этой плоскости, и найдем связь между координатами x, y, z в виде уравнения. Рассмотрим вектор  .

Векторы   и   ортогональны. Следовательно,   ·   = 0.

M(x - x₀) + N(y - y₀) + L(z - z₀) = 0 - уравнение плоскости, проходящей через данную точку, перпендикулярно данному вектору. Если раскрыть скобки в этом уравнении, то его можно привести Mx + Ny + Lz + К = 0,

где  К= - Mx₀ - Ny₀ - Lz₀. Следовательно, если плоскость задана общим уравнением Ax + By + Cz + D = 0, то вектор  (A,B,C) является вектором нормали к плоскости.

18

Уравнение плоскости в отрезках.  

Если в общем уравнении Ах + Ву + Сz + D = 0 поделить обе части на -D  , заменив  , получим уравнение плоскости в отрезках:    Числа a, b, c являются точками пересечения плоскости соответственно с осями х, у, z.

Уравнение плоскости, проходящей через заданную точку параллельно двум неколлинеарным векторам.

Пусть в координатном пространстве   заданы:

а) точка  ;

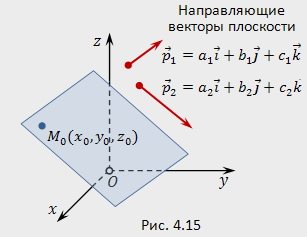
б) два неколлинеарных вектора 

Требуется составить уравнение плоскости, компланарной векторам   и проходящей через точку 

Выберем на плоскости произвольную точку  . Обозначим     — радиус-векторы точек   и   

Условие компланарности векторов   можно записать, используя свойства смешанного произведения   Применяя формулу, получаем уравнение плоскости, проходящей через заданную точку и компланарной двум неколлинеарным векторам:

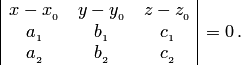
19

Определение 1

cos α⋅x+cos β⋅y+cos γ⋅z−p=0

называют нормальным уравнением плоскости или уравнением плоскости в нормальном виде. Реже его называют нормированным уравнением заданной плоскости. Для приведения уравнения плоскости Ax+By+Cz+D=0 к нормальному виду, обе части умножаются на нормированный множитель ±1/√A2+B2+C2. Знак определятся по числу D, он должен быть противоположным значения числа D.

Отклонением точки от плоскости называется расстояние от этой точки до плоскости, взятое со знаком “+”, если точка и начало координат O находятся по разные стороны от плоскости, иначе со знаком “–”. Если точка и начало координат O совпадают, то отклонение не определено или положительно.

Теорема 2

Отклонение точки от плоскости с уравнением (43) находится по формуле: (44).

Доказательство:

Докажем: .

, т.к. .

1. , когда направлен в то полупространство, где нет точки O.

2.

Теорема доказана

Следствие: (45)

(46)

Расстояние от точки до плоскости: