34 Классификация кривых второго порядка. Связь с инвариантами

1.b> 0элипсический тип

(x^2/a^2)+y^2/b^2=1 элипсис

2.b<0 гиперболический тип

(x^2/a^2)-y^2/b^2=1 гиперболы обе

(x^2/a^2)-y^2/b^2=-1

b=0 параболический тип

y^2=2rx парабола

35.Каноническое уравнение эллипсоида. Исследование формы методом сечений

Эллипсоид.

Рассмотрим сечение поверхности с плоскостями, параллельными xOy. Уравнения

таких плоскостей z=h, где h – любое число. Линия, получаемая в сечении,

определяется двумя уравнениями:

Если |h|>c, c>0, то точек пересечения поверхности с плоскостями z=h нет.

Если |h|=c, т.е. h=±c, то

36Гиперболоиды. Каноническое уравнение.. Исследование их формы методом сечений.

Однополостный гиперболоид.

Пересекая поверхность плоскостью z=h, получим линию пересечения, уравнения

которой имеют вид.

Полуоси достигают своего наименьшего значения при h=0, a₁=a, b₁

=b. При возрастании |h| полуоси будут увеличиваться.

Если пересекать поверхность плоскостями x=h или y=h, то в сечении получим

гиперболы. Найдем линию пересечения поверхности с плоскостью Oyx, уравнение

которой x=0. Эта линия пересечения описывается уравнениями:

Поверхность имеет форму бесконечно расширяющейся трубки и называется

однополостным гиперболоидом.

Двуполостный гиперболоид.

Если поверхность пересечь плоскостями z=h, то линия пересечение уравнениями

Если |h|<c, то плоскости z=h не пересекаются.

Если |h|=c, то плоскости h=±c касаются данной поверхности соответственно в

точках (0;0;с) и (0;0;-с).

Если |h|>c, то уравнения можно переписать в виде:

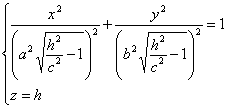
Эти уравнения определяют эллипс, полуоси которого возрастают с ростом |h|.

У обеих гипербол действительной осью является ось oz. Метод сечения позволяет

изобразить поверхность, состоящую из двух полостей, имеющих форму двух

неограниченных чаш. Поверхность называется двуполостным гиперболоидом.

37Параболоиды. Каноническое уравнение. Исследование их формы методом сечений

Параболо́ид ― тип поверхности второго порядка. Параболоид может быть охарактеризован как незамкнутая нецентральная (то есть не имеющая центра симметрии) поверхность второго порядка.Канонические уравнения параболоида в декартовых координатах: если и одного знака, то параболоид называется эллиптическим. если и разного знака, то параболоид называется гиперболическим. если один из коэффициентов равен нулю, то параболоид называется параболическим цилиндром Эллипти́ческий параболо́ид — поверхность, описываемая функцией вида , где и одного знака. Поверхность описывается семейством параллельных парабол с ветвями, направленными вверх, вершины которых описывают параболу, с ветвями, также направленными вверх. Если то эллиптический параболоид представляет собой поверхность вращения, образованную вращением параболы вокруг вертикальной оси, проходящей через вершину данной параболы. Гиперболи́ческий параболо́ид (называемый в строительстве «гипар») — седлообразная поверхность, описываемая в прямоугольной системе координат уравнением вида

. Из второго представления видно, что гиперболический параболоид является линейчатой поверхностью. Поверхность может быть образована движением параболы, ветви которой направлены вниз, по параболе, ветви которой направлены вверх, при условии, что первая парабола соприкасается со второй своей вершиной