Михайленко Е.В. Математика. Ч. 1. Элементы общей алгебры

Из вычислений видно, что остаток D(x), получившийся при делении равен нулю. То есть деление многочленов прошло без остатка.

Пример: Вычислить частное и остаток от деления полиномов x4 – 4x3 + 3 и x2 + 5x – 2.

Разделим полином x4 – 4x3 + 3 на полином x2 + 5x – 2.

В результате получим честное степени два и остаток степени один:

3.3. Бином Ньютона. Треугольник Паскаля Бином Ньютона.

Гениальный английский математик Исаак Ньютон (1643–1727) составил алгоритм, позволяющий возводить сумму двух слагаемых в степень с любым показателем. Данный алгоритм можно записать в виде алгебраического выражения, которое получило название бинома Ньютона:

a b n Cn0an Cn1an 1b ... Cnm an mbm ... Cnnbn .

Каждое m-тое слагаемое полинома n-й степени, полученного в правой части формулы, содержит произведение количества сочетаний из n по m и соответствующих степеней биномиальных слагаемых Cnm an mbm . Формулу можно записать, используя специальный знак суммы:

n

a b n Cni an ibi . i 0

Пример. Возвести в пятую степень выражение (2x – 1).

51

Решение. Используя формулу получим выражение, состоящее из шести слагаемых:

C50(2x)5( 1)0 C51(2x)4( 1)1 C52(2x)3( 1)2 C53(2x)2( 1)3 C54(2x)1( 1)4 C55(2x)0( 1)5 .

Вычисляя значения сочетаний и степеней, выражение преобразуется в следующий вид:

1 32x5 1 5 16x4 ( 1) 10 8x3 1 10 4x2 ( 1) 5 2x 1 1 1 ( 1).

Преобразуя каждое слагаемое, окончательно получим:

32x5 80x4 80x3 160x2 10x 1.

Пример. Раскрыть скобки и привести подобные члены в выражении

(3x + 2y)4.

Решение. Подставим выражение (3x + 2y)4в формулу бинома Ньютона:

C44 3x 4 2y 0 C43 3x 3 2y 1 C42 3x 2 2y 2 C41 3x 1 2y 3 C40 3x 0 2y 4 .

Рассчитаем числа сочетаний и коэффициенты при неизвестных:

1 81x4 1 4 27x3 2y 6 9x2 4y2 4 3x 8y3 1 1 16y4 .

Перемножив коэффициенты, получим:

81x4 216x3y 216x2 y2 96xy3 16y4 .

Пример. Найти коэффициент, стоящий перед x9 многочлена 2x 1,5 11. Решение. Зная алгоритм разложения двучлена 2x + 1,5 в 11-ую степень,

рассчитаем числовой коэффициент третьего слагаемого:

Треугольник Паскаля

Выдающийся французский ученый Блез Паскаль (1623–1662), работая с комбинаторными и алгебраическими задачами, выдвинул оригинальный метод упрощения расчета биномиальных коэффициентов. Суть метода сводится к построению треугольной таблицы, элементы которой являются числами сочетаний, использующихся в разложении степени биномов.

52

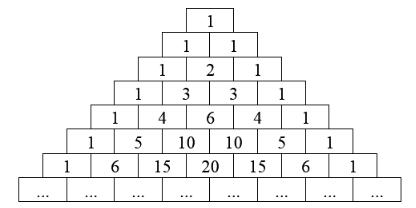
Треугольник Паскаля имеет следующий вид:

Несложно заметить, что все внутренние коэффициенты таблицы обладают следующим свойством: каждое число Треугольника Паскаля равно сумме двух чисел, над ним стоящих. Учитывая данное свойство можно неограниченно продолжать данную таблицу.

Пример. Раскрыть скобки и привести подобные слагаемые в выражении

a 2b 4 .

Решение. С помощью Треугольника Паскаля найдем биномиальные

Учитывая этот факт, подставим выделенные коэффициенты Треугольника Паскаля в формулу бинома Ньютона:

1 a4 2b 0 4 a3 2b 1 6 a2 2b 2 4 a1 2b 3 1 a0 2b 4

Упрощая данное выражение, получим:

a4 8a3b 24a2b2 32ab3 b4

3.4. Корни многочленов

Корнем многочлена P(x) называется число, при подстановке которого в многочлен выполняется тождество:

53

P(x) = 0.

Пример. Число 5/3 является корнем полинома 9x4 - 6x3 - 46x + 35, так как

9∙(5/3)4 – 6∙(5/3)3 – 46∙(5/3) + 35 = 0.

Теорема. Число корней (в том числе и комплексных) многочлена P(x) степени n, учитывая кратные корни равно n.

Пример. Число корней полинома x4 - 3x3 + 6x2 – 12x + 8 равно четырем. Из них два корня x1 = 1 и x2 = 2 являются действительными числами, а два корня x3 = –2i и x4 = 2i - комплексными.

Теорема. Полином P(x) = anxn + an-1xn-1 + … + a1x1 + a0 с вещественными коэффициентами a0, a1, …, an и корнями x1, x2, …, xn можно записать в виде:

P(x) = an(x – x1) (x – x2) … (x – xn).

Пример. Полином x4 - 3x3 + 6x2 – 12x + 8 можно записать как произведение:

(x – 1) (x – 2) (x + 2i) (x – 2i).

Для нахождения корней полиномов высоких степеней последовательно определяют очевидные корни и, используя теорему о разложении многочленов на множители, делят полиномы на x – xi.

Пример. Найдем корни полинома x5 + x4 – 5x3 – 7x2 + 10x.

Так как степень полинома равна 5, то он будет иметь ровно 5 корней. Очевидно, что одним из корней полинома является число 0.

Пусть x1 = 0. Разделим полином на бином x – x1 = x – 0 = x. В результате получим многочлен x4 + x3 – 5x2 – 7x + 10 степени 4.

Увидим еще один корень x2 = 1 и разделим новый полином на x – 1.

54

Очевидно, что одним из корней получившегося полинома 3-й степени x3 + 2x2 – 3x – 10

является число 2. Таким образом, x3 = 2. Разделим этот многочлен на x – 2.

В результате получим многочлен x2 + 4x + 5 степени 2. Найдем его корни.

Выпишем все полученные корни: {0; 1; 2; –2 – i; – 2 + i}.

Пример. Разложить на множители полином x4 + 4x3 – 31x2 – 46x + 168. Так как степень полинома равна 4, то он будет иметь ровно 4 корня. Очевидно, что одним из корней полинома является число 2. Пусть x1 = 2.

Разделим полином на двучлен x – 2.

В результате получим многочлен x3 + 6x2 – 19x – 84 степени 3.

55

Очевидно, что одним из корней получившегося полинома 3-й степени x3 + 6x2 – 19x – 84

является число 4. Таким образом, x2 = 4. Разделим этот многочлен на выражение x – 4.

В результате получим многочлен x2 + 10x + 21 степени 2. Найдем его корни.

D b2 4ac .102 4 21 1 16

Выпишем в порядке возрастания полученные корни: { -7; -3; 2; 4}.

56

Глава 4. Матрицы и определители

При изучении различных по природе и физическим характеристикам явлений или процессов исследователь часто имеет дело с целым набором различных данных, которые оформляются в виде числовых прямоугольных таблиц. Дальнейшая обработка этих данных, анализ полученных результатов также предполагает работу с табличными формами.

Методы математической статистики, математического моделирования, построения прогнозов предполагают глубокую аналитическую работу по исследованию этих таблиц, выполнению различных операций и преобразований с комплексами этих данных.

Для математической обработки числовых таблиц введено понятие матрицы, представляющей числовой двумерный массив. Для матриц установлены преобразования, определены алгебраические операции, предложены оценки их качественных характеристик.

4.1. Основные понятия матричного счисления Понятие матрицы

Определение. Матрицей называется прямоугольная таблица чисел, содержащая m строк и n столбцов.

Числа m и n называются порядками матрицы. В случае если m = n, матрица называется квадратной, а число m = n – ее порядком.

Для записи матрицы обычно применяются круглые скобки, а для краткого обозначения матрицы часто используются заглавные латинские буквы:

Числа aij, входящие в состав данной матрицы, называются ее элементами. В записи aij первый индекс i означает номер строки, а второй индекс j – номер столбца.

57

Элементы матрицы могут иметь любые значения из множества действительных чисел.

Пример. Ниже представлена матрица порядков 3х2.

Две матрицы считаются равными, если они имеют одинаковые порядки и все их соответствующие элементы совпадают.

Матрица называется нулевой порядков m и n, если все ее элементы равны нулю. Она обозначается символом O. В качестве примера приведем нулевую матрицу порядков 2 и 3.

Пример. Нулевая матрица порядков 2х3.

Квадратные матрицы

Матрица называется квадратной, если ее порядки совпадают. В этом случае количество строк матрицы совпадает с количеством ее столбцов.

В случае квадратной матрицы вводятся понятия главной и побочной диагоналей. Главной диагональю квадратной матрицы называется диагональ a11, a22, …, ann, идущая из левого верхнего угла этой матрицы в правый нижний ее угол. Побочной диагональю той же матрицы называется диагональ an1, a(n-1)2, …, a1n, идущая из левого нижнего угла в правый верхний угол:

Среди квадратных матриц отметим, так называемые, симметричные матрицы. Действительно, для таких матриц наблюдается симметрия

58

относительно их главных диагоналей. Таким образом, для каждой пары элементов aij и aji. симметричной матрицы А выполняется равенство:

aij = aji.

Пример. Симметричная матрица порядков 4х4.

Еще одним классом квадратных матриц являются треугольные матрицы. Матрица А называется верхней треугольной, если все ее элементы, находящиеся ниже главной диагонали, равны нулю, и соответственно нижней треугольной, если все ее элементы, находящиеся выше главной диагонали, равны нулю.

Пример. Ниже представлены верхняя треугольная матрица B и нижняя треугольная матрица С.

Среди квадратных матриц выделим класс так называемых диагональных матриц, у каждой из которых элементы, расположенные вне главной диагонали, равны нулю. Каждая диагональная матрица порядка n имеет вид:

где d1, d2, ..., dn –произвольные числа.

В классе всех диагональных матриц рассмотрим матрицы с совпадающими элементами di, то есть такие матрицы у которых элементы главной диагонали равны между собой: d1 = d2 = ... = dn.

59