
Михайленко Е.В. Математика. Ч. 1. Элементы общей алгебры
.pdf
x |
2 2i |
|
2 2i |
1 i , x |
2 |
|
2 2i |
|
2 2i |
1 i . |
|
|
|
|
|
||||||||
1 |
2 |
1 |
2 |
|
|
2 1 |
2 |
|
|||
|
|
|
|
|
|||||||
|
|
|
Тригонометрическая форма комплексного числа |
||||||||
|
По |
формулам |
x r cos , |
y r sin , |
связывающих полярные и |
||||||
прямоугольные координаты, получим тригонометрическую форму записи комплексного числа z x iy :
|
|
|
|
|
z r cos isin , |
|
|
|
|
|
|
|
|
|
||||||||||||
где r – модуль, а число – аргумент комплексного числа z . |
|
|
|
|
|
|
||||||||||||||||||||
Модуль r |
|
z |
|
вычисляется по формуле r x2 |
y2 . |
|
|
|
|
y |
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
Аргумент Arg z определяется из формул cos |
x |
, sin |
|
, tg |
|
y |
, где |
|||||||||||||||||||
|
r |
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r |
|
|
|
|
x |
||||
|
|
|
|
|
|
y |
, |
при x 0, |
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
arctg |
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Arg z , |
|
|
, при x 0,y |
0, |
|
|
|
|
|
|
|
|||||||||||||||
Arg z arctg |
|
|
|
|
|
|
|
|
|
|||||||||||||||||
x |
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
, при x 0,y |
0. |
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
arctg |
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
x |
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Пример 1.26. Представить в тригонометрической форме комплексное |
||||||||||||||||||||||||||
число z 2 4i . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Решение. |
Для комплексного |
|
|
числа |
z 2 4i , |
где |
Rez x 2 0, |
|||||||||||||||||||
Imz y 4 0, |
модуль равен |
|
|
z |
|
|
|
2 4i |
|
|
22 |
42 |
|
4 16 |
20 2 5, |
|||||||||||
|
|
|
|
|
||||||||||||||||||||||
аргумент равен Arg z arctg 42 arctg2.
Следовательно, z 2 4i 2 5 cos arctg2 i sin arctg2 .
5 cos arctg2 i sin arctg2 .
Рассмотрим действия над комплексными числами в тригонометрической
форме. |
|
|
|
|
|
|
1. Произведением |
комплексных |
чисел |
z1 r1 cos 1 |
i sin 1 |
и |
|
z2 r2 cos 2 |
i sin 2 |
называется |
число, |
определяемое |
равенством |
|
z r1r2 cos 1 |
2 i sin 1 2 . |
|
|
|
|
|
Действительно, используя тригонометрические равенства, имеем
21

z1 z2 r1 cos 1 i sin 1 r2 cos 2 isin 2
r1r2 cos 1 cos 2 i cos 1sin 2 i sin 1 cos 2 i2 sin 1sin 2
r1r2 cos 1 cos 2 sin 1sin 2 i cos 1sin 2 sin 1 cos 2
r1r2 cos 1 2 isin 1 2 .
Пример 1.27. Найти произведение чисел z1 3 cos10 i sin10 и z2 2 cos40 i sin 40 .
Решение.
z1 z2 3 cos10 i sin10 2 cos 40 i sin 40
6 cos10 cos 40 i2 sin10 sin 40 i cos10 sin 40 i sin10 cos 40
6 cos10 cos 40 sin10 sin 40 i cos10 sin 40 sin10 cos 40
6 cos50 i sin 50 .
2. Частным |
z1 |
комплексных |
чисел |
z1 r1 cos 1 i sin 1 |
и |
|
z2 |
||||||
|
|
|
|
|
||
z2 r2 cos 2 i sin 2 |
(z2 0) называется |
число, |
определяемое равенством |
|||
zr1 cos 1 2 isin 1 2 .
r2
Действительно, используя тригонометрические равенства, имеем
|
|
|
|
z |
|
|
z1 |
|
r1 |
cos 1 i sin 1 |
|
r1 |
cos 1 |
isin 1 |
cos 2 |
|
i sin 2 |
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
z |
2 |
|
|
r |
cos |
2 |
isin |
2 |
|
|
|
|
r |
|
cos |
2 |
isin |
2 |
cos |
2 |
i sin |
2 |
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
cos |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
r |
|
|
cos |
2 |
i2 sin sin |
2 |
i cos |
|
sin |
2 |
i sin cos |
2 |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
1 |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
r2 |
|
|
|
|
|
|
|
|
|
|
|
cos 2 cos 2 i2 sin 2 sin 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
r1 |
|
|
cos 1cos 2 |
sin 1sin 2 i sin 1cos 2 cos 1sin 2 |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
r |
|
|
|
|
|
|
|
|
|
|
|
cos |
2 |
cos |
2 |
|
sin |
2 |
sin |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
r1 |
|
cos 1 |
2 isin 1 |
2 |
|
|
r1 |
|
cos |
2 |
isin |
2 |
. |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
r2 |
|
|
cos2 2 |
sin2 2 |
|
|
|
|
|
|
r2 |
|
|
|
|
1 |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
Пример |
|
|
1.28. |
|
|
Найти |
|
|
|
|
частное |
|
|
чисел |
z1 |
|
|
|
|
i sin |
|
|
и |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 cos |
3 |
3 |
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
3 |
i sin |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
z2 7 cos |
|
5 |
5 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
22 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|

Решение. Применим формулу для нахождения частного двух комплексных чисел, заданных в тригонометрической форме,
|
|
|
|
|
|
|
|
|
|
|
|
|
|
isin |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z |
|
5 cos |
3 |
3 |
|
|
|
5 |
|
|
|
|
|
3 |
|
|
3 |
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
cos |
|
|
i sin |
|
|
|
|
|
|
||||
|
|
|
|
z |
|
|
|
|
|
3 |
|
|
3 |
|
7 |
3 |
3 |
|
|||||||||||||||||
|
|
|
|
2 |
|
|
|
|
i sin |
|
|
|
|
|
|
5 |
|
|
|
5 |
|
|
|||||||||||||
|
|
|
|
|
|
|
7 cos |
|
5 |
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
5 |
|
|
|
|
|
|
3 |
|
|
|
|
|
3 |
|
|
5 |
|
|
|
|
4 |
|
|
4 |
|
|
||||||||
7 |
cos |
3 |
|
5 |
|
isin |
3 |
5 |
|
|
7 |
cos |
|
isin |
15 |
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
15 |
|
|
|
|
|
||||||||||
|
5 |
|
|
|
|
4 |
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
7 |
cos |
|
|
i sin |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
15 |
|
|
|
|
15 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
3. Возведение |
комплексного |
числа |
z r cos i sin |
в натуральную |
||||||||||||||||||||||||||||
степень n осуществляется по формуле
zn rn cos n i sin n –
формула Муавра.
Пример 1.29. Вычислить 1 i 3 12 .
3 12 .
Решение. Запишем число z 1 i 3 в тригонометрической форме, для этого вычислим модуль и аргумент комплексного числа z :
3 в тригонометрической форме, для этого вычислим модуль и аргумент комплексного числа z :
Rez x 1 0, |
|
Imz y 3 0, |
|
|
|
|
|
|
2 |
|
|
2 |
|
|
|
|
|
|
, |
|||||||||||
|
|
|
|
|
|
3 |
|
|
|
|
|
2 |
|
r |
|
z |
|
|
1 |
|
|
3 |
|
1 |
|
3 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Arg z arctg |
1 |
|
3 |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Комплексное |
|
число |
в |
|
тригонометрической |
форме |
имеет |
|
|
вид |
||||||||||||||||||||
|
|
2 |
i sin |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
z 2 cos |
3 |
3 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Применим формулу Муавра |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
z |
12 |
|
|
|
|
2 |
i sin |
2 |
12 |
|
12 |
|
|
|
2 |
|
|
|
|
2 |
|
|
|
|
|
|
|
|||
|
|
2 cos |
3 |
3 |
|
|
2 |
cos 12 |
3 |
|
isin 12 |
3 |
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
2 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
i 0 4096. |
|
|
|||||||
212 cos 12 |
3 |
i sin 12 |
3 |
|
4096 cos 8 i sin 8 40961 |
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
23

4. Извлечение |
из |
комплексного |
|
числа |
z r cos i sin |
корня |
n -ой |
|||||||||||||||||||||||
степени осуществляется по формуле |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
n |
|
|
|
|
|
2 k |
isin |
2 k |
, |
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
z n r cos |
|
n |
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
k 0,1,2,...,n 1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Пример 1.30. Вычислить 3 |
3 i . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Решение. Запишем число |
z |
|
3 i в |
тригонометрической |
|
форме, |
|
для |
||||||||||||||||||||||
этого вычислим модуль и аргумент комплексного числа z : |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
Rez x 3 0, |
|
Imz y 1 0, |
|
|
r |
|
z |
|
|
|
|
3 2 12 |
|
3 1 2, |
||||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Arg z arctg |
1 |
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Комплексное число в тригонометрической форме имеет вид |
z 2 |
|
|
|
i sin |
|
|
|||||||||||||||||||||||
cos |
3 |
3 |
. |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 k |
|
|
|
|
|
2 k |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Таким образом, |
3 |
|
|
|
|
|
|
|
3 2 cos |
3 |
|
|
i sin |
3 |
|
|
|
, |
||||||||||||
3 i 3 2 cos |
|
i sin |
|
|
|
|
|
|
|
|||||||||||||||||||||
3 |
3 |
|
|
3 |
|
3 |
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k 0,1,2, откуда получаем три значения корня z1, z2, z3 : при k 0
|
|
|
|
|
|
|
|
2 0 |
|
|
|
2 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
3 |
|
3 |
|
|
3 |
|
3 |
|
3 |
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
2 |
cos |
|
i sin |
|
|
|
|
|
|
|
|
|
||||||||||||
z |
1 |
z |
|
|
|
2 |
cos |
|
i sin |
|
|
|
; |
|
|
||||||||||||
|
|
3 |
|
|
3 |
|
9 |
9 |
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
при k 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
2 1 |
|
|
|
2 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
3 |
|
|
|
3 |
|
|
3 |
|
3 |
|
|
7 |
|
|
|
7 |
|
||||||
|
|
|
2 cos |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
z |
2 |
z |
|
|
i sin |
|
|
|
2 |
cos |
|
|
i sin |
|
|
|
|
; |
|||||||||
|
3 |
|
3 |
|
9 |
|
|
9 |
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
при k 2
24
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
3 |
|
3 2 2 |
|
3 2 2 |
|
|
3 |
|
13 |
|
13 |
|
z3 |
|
z |
|
|
2 cos |
|
i sin |
|
|
|
|
2 cos |
|
i sin |
|
. |
|
|
3 |
3 |
|
9 |
9 |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Показательная (экспоненциальная) форма комплексного числа |
|
||||||||||||
|
Используя формулу Эйлера |
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
ei cos i sin , |
|
|
|
|
|
|
|||
комплексное число z r cos isin можно записать показательной форме |
||||||||||||||||
|
|
|
|
|
|
|
|
z rei , |
|
|
|
|
|
|
|
|
где r |
– модуль, а число – аргумент комплексного числа z . |
|
|
|
||||||||||||
|
Пример 1.31. Представить в |
показательной |
форме комплексное |
число |
||||||||||||
z 4 3i .
|
|
|
|
Решение. |
|
Для |
комплексного |
|
числа z 4 3i |
, |
где |
|
Rez x 4 0, |
|||||||||||||||||||||||||||
Imz y 3 0, |
|
|
|
модуль |
|
|
|
равен |
|
z |
|
|
|
|
4 3i |
|
|
4 2 |
|
3 2 |
|
16 9 |
||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
25 5, аргумент равен Arg z arctg |
3 |
arctg 3 |
. |
|
|
|
|
|
||||||||||||||||||||||||||||||
4 |
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Следовательно, z 4 3i |
|
|
|
i arctg |
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
5e |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
Пример 1.32. Изобразить на комплексной плоскости C множество точек, |
||||||||||||||||||||||||||||||||||||
удовлетворяющих условию: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
а) |
|
z |
|
2, |
|
|
|
|
|
|
|
|
б) i Im z i , |
|
|
|
|
|
|
в) 0 Re z 2, |
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z |
|
1, |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
г) |
Arg z |
, |
|
|
|
|
д) |
|
z |
|
3, |
|
|
|
|
|
|
|
|
|
|
|
|
е) |
|
|
|
|
|
|
3 |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Arg z |
. |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|||
|
|
|
|
Решение. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
а) Так как |
|
z |
|
|
x2 y2 , тогда |
|
x2 y2 |
2 или |
|
|
|
|
|
y |
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
x2 y2 4. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2i |
|
|
|
|||||||||
Множество |
точек, |
|
удовлетворяющих |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
условию |
|
z |
|
|
2, образует круг радиуса 2 с центром в |
|
-2 |
|
|
0 |
2 |
x |
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
начале координат. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
-2i |
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
25 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|

б) Условие i Im z i можно представить как
i y i .
в) Условие 0 Re z 2 можно представить как
0 x 2.
г) Множество точек Arg z 4 лежат на луче,
выходящем из начала координат под углом |
|
|
к |
|
|
4 |
|
действительной оси Ox . |
|
|
|
д) Множество точек расположено внутри и на границе круга радиуса z 1 и заключено между
лучами Arg z 6 и Arg z 34 .
1.6. Системы счисления
y i
0 |
x |
|
|
-i |
|
y
0 |
2 x |
y
|
|
4 |
|
0 |
x |
y
i
-1 |
0 |
1 x |
-i
Системой счисления называется совокупность приемов и правил представления чисел с помощью цифровых знаков. Системы счисления можно разделить на непозиционные и позиционные. Знаки, используемые при записи чисел, называются цифрами.
В непозиционных системах счисления от положения цифры в записи числа не зависит величина, которую она обозначает. Примером непозиционной системы счисления является римская система. В римской системе в качестве цифр используются латинские буквы:
Буквы |
I |
V |
X |
|
L |
C |
D |
M |
Цифры |
1 |
5 |
10 |
|
50 |
100 |
500 |
1000 |
|
|
|
|
26 |
|
|
|
|

Пример 1.33. Число CCXXXII складывается из двух сотен, трех десятков
идвух единиц и равно двумстам тридцати двум.
Впозиционных системах счисления величина, обозначаемая цифрой в записи числа, зависит от ее позиции. Количество используемых цифр называется основанием позиционной системы счисления. Основанием системы счисления может быть любое натуральное число большее 1.
Система счисления с основанием равным 1 называется унарной.
Для записи чисел в позиционной системе с основанием n нужно иметь
алфавит из n цифр. Обычно для этого при n 10 используют n первых арабских цифр, а при n 10 к десяти арабским цифрам добавляют буквы.
Пример 1.34. Приведем алфавиты некоторых систем:
Основание |
Название |
Алфавит |
n 2 |
Двоичная |
0 1 |
n 3 |
Троичная |
0 1 2 |
n 4 |
Четверичная |
0 1 2 3 |
n 5 |
Пятеричная |
0 1 2 3 4 |
n 6 |
Шестеричная |
0 1 2 3 4 5 |
n 7 |
Семеричная |
0 1 2 3 4 5 6 |
n 8 |
Восьмеричная |
0 1 2 3 4 5 6 7 |
n 9 |
Девятеричная |
0 1 2 3 4 5 6 7 8 |
n 10 |
Десятеричная |
0 1 2 3 4 5 6 7 8 9 |
n 16 |
Шестнадцатеричная |
0 1 2 3 4 5 6 7 8 9 A B C D E F |
Основание системы счисления, в которой записано число, обычно обозначается нижним индексом. Например, 5557 – число, записанное в семеричной системе счисления. Если число записано в десятичной системе, то основание, как правило, не указывается. Основание системы – это тоже число, и его указывают в обычной десятичной системе.
Всякое число N в позиционной системе счисления с основанием m можно представить в виде полинома
l aimi 1 aimi 1 ai 1mi 2 ..... a1m0,
i 1
где l – количество разрядов числа,
27
i – порядковый номер разряда,
m – основание системы счисления,
ai – множитель, принимающий любые целочисленные значения от 0 до m 1 и соответствующий цифре в i -й позиции числа.
Пример 1.35. Записать число 629310 в форме многочлена.
Решение. Над цифрами числа 6293 напишем порядковые номера разрядов.
3 21 0
629310 629310 6 103 2 102 9 101 3 100.
Соответствие между первыми несколькими натуральными числами основных систем счисления представлено в таблице:
Десятичная |
Двоичная |
Восьмеричная |
Шестнадцатеричная |
система |
система |
система |
система |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
2 |
10 |
2 |
2 |
3 |
11 |
3 |
3 |
4 |
100 |
4 |
4 |
5 |
101 |
5 |
5 |
6 |
110 |
6 |
6 |
7 |
111 |
7 |
7 |
8 |
1000 |
10 |
8 |
9 |
1001 |
11 |
9 |
10 |
1010 |
12 |
A |
11 |
1011 |
13 |
B |
12 |
1100 |
14 |
C |
13 |
1101 |
15 |
D |
14 |
1110 |
16 |
E |
15 |
1111 |
17 |
F |
16 |
10000 |
20 |
10 |
Связь двоичной и десятичной систем счисления
1. Для перевода числа из двоичной системы счисления в десятичную необходимо его записать в виде многочлена, состоящего из произведений цифр числа и соответствующей степени числа 2, и вычислить по правилам десятичной арифметики:
28
X 2 an 2n 1 an 1 2n 2 an 2 2n 3 ... a2 21 a1 20
При переводе удобно пользоваться таблицей степеней двойки:
n |
0 |
|
1 |
2 |
|
3 |
4 |
|
5 |
6 |
|
7 |
8 |
9 |
|
10 |
|
2n |
1 |
|
2 |
4 |
|
8 |
16 |
|
32 |
64 |
128 |
256 |
512 |
1024 |
|
||
Пример |
1.36. |
Число |
111010002 |
перевести |
в |
десятичную |
систему |
||||||||||
счисления.
Решение.
87654 3 2 1
111010002 1 27 1 26 1 25 0 24 1 23 0 22 0 21 0 20 23210
.
2. Для перевода десятичного числа в двоичную систему счисления его необходимо последовательно делить на 2 до тех пор, пока не останется остаток, меньший или равный 1. Число в двоичной системе записывается как последовательность последнего результата деления и остатков от деления в обратном порядке.
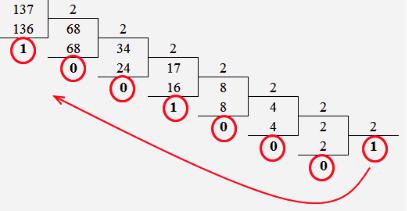
Пример 1.37. Число 13710 перевести в двоичную систему счисления. Решение. Разделим число 137 последовательно на «2» и выпишем все
остатки начиная снизу вверх.
Следовательно, 13710 100010012 .
29
Глава 2. Теория чисел 2.1. Основные понятия теории чисел
Теория чисел занимается изучением свойств целых чисел.
Целыми будем называть числа натурального ряда 1, 2, 3, ...
(положительные целые), числа им противоположные -1, -2, -3, ...
(отрицательные целые) и 0 (ноль).
Сумма, разность и произведение двух целых a и b будут также целыми, но частное от деления a на b (если b не равно нулю) может быть как целым, так
идробным.
Вслучае, когда частное от деления a на b - целое, обозначая его буквою d, имеем a = b d, говорят, что a делится на b или что b делит a. При этом а называем кратным числа b и b - делителем числа а.
Пример. Найти четыре числа, кратные числу 12.
Такими числами могут быть числа, которые делятся на 12, например, -24, 60, 804, 14808.
Пример. Определить все делители числа 30.
Выпишем все числа, на которые нацело делится число 30 в порядке возрастания: -30, -15, -10, -6, -5, -3, -2, -1, 1, 2, 3, 5, 6, 10, 15, 30.
Имеют место следующие теоремы делимости. Теорема 1. Если а кратно m, m кратно b, то а кратно b.
Пример. Число 1716 кратно 156, а 156 кратно 13, значит 1716 кратно 13. Теорема 2. Если в равенстве вида к + 1+ ... + п = р + q + ... + b относительно всех членов, кроме какого-либо одного известно, что они кратны
b, то и этот один член кратен b.
Пример. В равенстве 204 + 238 + 179 + 187 + 119 = 153 +765 все числа левой части 204, 238, 179, 187, 119 и справа 153 очевидно делятся на 17, следовательно, 765 тоже делится на 17.
3. Всякое целое а представляется единственным способом через положительное целое b в виде:
a = bq + r, где 0 ≤ r < b
30
