Добавил:

ivanov666 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Сибирская государственная автомобильно-дорожная академия

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

2492.pdf

Скачиваний:

Добавлен:

07.01.2021

Размер:

12.89 Mб

Скачать

☆

<<< < Предыдущая 1 23 / 103 4 5 6 7 8 9 10 > Следующая >>>

§3. Орт и направляющие косинусы

Ортом вектора a называется вектор а о , имеющий то же н а- правление, что и a , и модуль, равный 1:

ао =1; а о ↑↑ а .

ао = а1 а − орт вектора a .

Если

а = (x,

y, z),

то координаты орта находятся по формуле

(рис. 11)

о =

+ y

+ z

+ y

+ z

+ y

+ z

Рис. 11

Направляющие косинусы

вектора

−

это

косинусы углов

α, β, γ , которые вектор a образует с осями координат.

= cos (a, Ox);

cosα

= cos (a, Oy);

cos β

cosγ

= cos (a, Oz).

cosα =

;cos β =

;cosγ =

x2 + y2 + z2

Заметим, что a o = (cosα, cos β, cosγ ), т.е. координаты орта равны направляющим косинусам.

Основное свойство косинусов

cos2 α + cos2 β + cos2 γ =1.

Пример. Найти орт вектора: a = 3i + 4 j −12 k . Решение. Найдём длину a :

a = 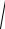32 + 42 + (−12)2 = 169 = 13.

Поэтому a o =

−

Задачи для самостоятельного решения

Даны

координаты

вершин

треугольника

A(1, 2, 3); B(3, 2, 1); C(1, 4, 1). Показать, что треугольник равносторон-

ний.

Вычислить модульбвектора

a = i

+ 2

− 1 (4i

+ 8

+ 3

) и

найти его направляющие косинусы.

Даны точки M1(1, 2, 3) и M 2 (3, − 4, 6). Найти длину и направ-

ление вектора

M1M

Дан вектор

a = 4

− 2

+ 3

Найти вектор b ,

если

первая координата b равна 0, вторая координата b равна второй координате a .

5. Радиус-вектор точки M составляет с осью Oy угол 60 , а с

осью Oz − угол 45 , его длина равна 8. Найти координаты M , если её абсцисса отрицательна.

6. Найти орт вектора a = i − 2 j − 2 k .

Ответы:

2.	a	=	3	; cosα =			1	; cos β = cosγ =			2 .
2.	a	=	3	; cosα =			1	; cos β = cosγ =			2 .
			5				3		6		3
			5				3				3
3. 7; cosα =					2	; cos		β = −		; cosγ =	3 .
					7				7		7

4.b = −2 j + 5k или b = −2 j − 5k .

5.M (− 4; 4; 42).

6.13 i − 23 j − 23 k .

Вопросы и задания для самопроверки [1,2,4,6]

1.Что называется координатами вектораИв декартовой прямоугольной системе координат (ДПСК)?

2.Сформулируйте теорему о разложенииД вектора по ортам координатных осей.

3.Дайте определение направляющихА косинусов вектора.

4.Какое основное свойство направляющих косинусов вектора?

5.Сформулируйте условиебколлинеарности векторов.и

ется число, равное

cos(a,

или

(проекция

на a )=

Пр

a =

Прa

Свойства:

a b = ba (коммутативность);

(α a ) (bβ )= (α β ) (ab) (сочетательность);

a (b + c )= a b + a c (дистрибутивность).

Действительно, a (b + c )= a Прa (b + c )= a (Прa b + Прa c )=

= a Прa b + a Прa c = a b + a c .

Критерий перпендикулярности (ортогональности) ( ) векторов

= 0 .

Основное использование:

1. a a =

2 ;

− нахождение длины вектора.

a a

a b

2. cos(a,

− нахождение угла между векторами.

Теорема (вычисление скалярного произведения).

Если a = (x , y , z

) и b = (x

Д, z ) − два вектора, то их скаляр-

ное произведение находится по формуле

+ z1 z2 .

a b = x1 x2 + y1 y2

Доказательство.

Запишем векторы a , b в виде линейной комбинации базисных:

+ y1

+ z1

= x1i

= x2 i

+ y2 j + z2 k .

Тогда

a b = (x1i + y1 j + z1k) (x2 i + y2 j + z2 k)= x1x2i i + x1 y2i j +

+ x1z2i k + y1x2 ji + y1 y2 j j + y1z2 j k + z1x2 k i + z1 y2 k j + z1z2 k k =

= x1x2 + y1 y2 + z1z2 .

Здесь использованы скалярные произведения базисных векторов:

i j = i k = j k = 0, т. к. i j k ; i i = i 2 =12 =1; j j =1; k k =1.

Примеры.

1. Найти скалярное произведение векторов

a = 3i

+ 4 j + 7 k и b = 2i − 5 j + 2 k .

Решение.

Находим

= 3 2 + 4 (− 5)+ 7 2 = 0 .

Так как

скалярное

произведение векторов a

= 0; a ≠ 0;

≠ 0, то a

. Векторы a и

ортогональны.

2. Даны векторы a = mi

+ 3 j + 4k и b = 4i

+ m j − 7k . При каком

значении

m эти векторы перпендикулярны?

Решение.

Находим

скалярное произведение

этих

векторов:

a b = 4m + 3m − 28 = 0. Так как a

, то a

= 0. Отсюда 7 m − 28 = 0 ,

m = 4 .

3. Найти

(5 a + 3

)(2 a −

), если

= 2;

= 3; a

Решение. (5 a + 3

)(2 a −

)= 10 a 2

− 5 a

+ 6 a

− 3

2 =

= 10 a 2 + a

− 3

= 10 22 + 0 − 3 32 = 40 − 27 = 13.

a b

0 при a b.

Здесь использованыбсвойства a 2

= a 2 = 22 ; a b =

4. Определить угол между векторами

a = i

+ 2 j + 3k и b = 6i + 4 j − 2 k.

Решение. Так как a

cosϕ , то cosϕ =

Имеем

= 1 6 + 2 4 + 3 (− 2) = 8;

= 2

1 + 4 + 9

14;

36 +16 + 4

14;

cosϕ =

= 2 и ϕ = arccos

2 .

2 14

14 2

5. Дана сила F{− 5, −1, − 4 } , точки A(− 2,3,6) и B(1,5, − 3). Ка-

кую работу производит сила F , когда точка ее приложения, двигаясь прямолинейно, перемещается из точки А в точку В?

Решение. Работа силы равна скалярному произведению вектора силы F на вектор перемещения AB = {1+ 2; 5 − 3; − 3 − 6}= {3; 2; − 9}. Находим работу:

А= F AB = −5 3 + (−1) 2 + (−4) (−9) = −15 − 2 + 36 = 19 .

Задачи для самостоятельного решения

1. Найти скалярное произведение векторов

3a − 2b и 5 a − 6b ,

если

a = 3i

+ 4 j + 5k и b = 4i + 5 j − 3k .

3. При каком значении m векторы a = mi + j и b = 3i − 3 j + 4k

перпендикулярны

иб

2a + 3b + 4c и 5a + 6b + 7c ,

если

= 1;

= 2;

= 3; (a,

(a,c )(

,c )= π .

+ 2

+ 3 j + 2k . Найти Прa b

5. Даны векторы a = 2i

= 6i

и Пр

a .

F{3;1, − 4 };

A(2,0,1); B(1, 4, − 2).

6. Дана сила F , точки А и В:

Какую работу производит сила F , когда точка ее приложения, двигаясь прямолинейно, перемещается из точки А в точку В?

Ответы:

1.336 .

2.arccos 17 .

3.1.

4.547.

5.203 и 207 .

6.13.

Вопросы и задания для самопроверки [1,2,3,4,6]

1.Определите скалярное произведение векторов.

2.Как выглядит критерий перпендикулярности векторов?

3.Напишите формулу для вычисления через координаты скалярного произведения векторов.

4.Каков геометрический смысл скалярного произведения?

5.Чему равно скалярное произведениеИj k ?

6.Что называется скалярным произведением n-мерных векторов? ДА

c = a × b (c = [a,b]) (см. прил. 4), удовлетворяющий условиям:

1) c

= a

b sin (a,b) − дл на векторного произведения;

2) с

− вектор

с перпендикулярен плоскости векторов

a и

;

с = a ×

x	0	y
x

а	б
	Рис. 12

3) с расположен по отношению к векторам a и b так же, как

ось OZ к осям OX и OY (рис. 12).

Направление вектора с определяется правилом буравчика (правого винта).

Свойства:

a × b = −(b × a ) (антикоммутативность);

(α a )× (β b)= α β (a × b) (сочетательность); a × (b + c )= a × b + a × c (дистрибутивность).

Критерий коллинеарности

a ||

a ×

= 0 .

Замечание. Если известны координатыИвекторов, то для провер-

ки их коллинеарности можно проверить пропорциональность коорди-

нат.

Пример. Известны координаты векторов:

a = (3;1; 4);

= (6; 2; 8); c = (6; 3; 8).

Так как

= 1 = 4

, то a ||

;

≠ 1 ≠

4 , то

a || c .

2и8

Теорема (геометрический смысл векторного произведения).

Пусть a и b имеют общее начало. Тогда длина векторного произведения векторов равна площади параллелограмма, построенного

на a и b .

Доказательство.

Вспомним формулу площади параллелограмма (рис. 13):

Sпар = a b sin (a,b).

Рис. 13

Заметим, что по определению векторного проиведения

a × b = a b sin (a,b), т. е. Sпар = a × b .

Основное использование

Sпар =

a ×

S∆ = 1

a ×

Теорема (выражение векторного произведения векторов че-

рез их координаты).

Пусть a = (x1, y1, z1 ) и

= (x2 , y2 , z2 ). Тогда

a ×

x2 y2

Доказательство.

Составим таблицу векторных произведений базисных векторов:

× i = 0 ;

× j = k ;

i × k = − j ;

= −

;

× i

= i

;

× i

= −i

Для запоминания таблицы удобна «шпаргалка»:

i j k i

−

(рис. 14).

Рис. 14

Докажем теорему. По условию, a = x1 i + y1 j + z1 k и b = x2 i + y2 j + z2 k . Имеем

a × b = x1 x2 (i × i )+ x1 y1 (i × j )+ x1 z2 (i × k )+ y1 x2 ( j × i )+ y1 y2 (j × j )+

+ y1 z2 (

)+ z1 x2 (

)+ z1

y2 (

)+ z1

z2 (

× i

+ x1 z2 (−

)+ y1 x2 (−

)+ y1 z2 i

(− i

= x1 y2

+ z1 x2

+ z1

= (y1

z2 − z1

y2 )i

+ (− x1 z2 + z1

x2 )

+ (x1

− y1

x2 )

;

−

;

= i

− j

+ k

Для демонстрации

видео

нажмите на кнопку

https://www.youtube.com/watch?v=go0HWBnuPqs

y1 = y2

Примеры.

1. Пусть a = (1; −1; 0); b = (2;1; −1) − координаты двух векторов. Тогда их векторное произведение равно

= (1;1; 3).

а ×

−1 0

+ 3

, т. е. a ×

= i

−1

2. Найти векторное произведение векторов

a = 2i + 3 j + 5k и b = i + 2 j + k.

Решение. Имеем

a ×

3 5

2 5

2 3

2 3 5

−

= −7

+ 3

= i

3. Вычислить площадь параллелограмма, построенного на век-

торах

− 2 j

6k.

a = 6i

+ 3 j − 2k

и b = 3i

Решение. Находим векторное произведение векторов a и

a × b =

6 3

− 2

= i

− 2

− j

6 − 2

+ k

6 3

− 2

3 − 2

− 2 6

− 42 j − 21k.

= 14i

Так как Sпар

a ×

, то

= 49(кв.ед.).

пар

142 + (− 42)2

+ (− 21)2

4. Вычислить

площадь

треугольника с

вершинами

A(1,1,1);

B(2, 3, 4); C(4, 3, 2).

Решение. Находим векторы AB и AC :

AB = (2 −1)i + (3 −1)j + (4 −1)k = i + 2 j + 3k ;

AC = (4 −1)i + (3 −1)j + (2 −1)k = 3i + 2 j + k .

Известно, что S∆

= 1

Sпар

= 1

. Найдём

2 3

1 3

1 2

1 2 3

= i

− j

+ k

= −4i + 8 j − 4k .

Следовательно,

S∆ = 1

(кв.ед.).

16 + 64 +16

5. Вычислить площадь параллелограмма, построенного на век-

торах a + 3

и 3a +

, если

=1;

(a,

)

= 30 .

Решение. (a + 3

)× (3a +

)= 3a

× a

+ a ×

+ 9

× a + 3

(Используем свойства векторного произведения:

a × a = 0;

= 0; a ×

= −

× a )

= 3

0 + a ×

− 9 a ×

+ 3

0 = −8a ×

Sпар =

− 8a ×

= 8

a ×

= 8

sinϕ = 8 1 1 sin30 = 8 1 = 4(кв.ед.).

6. Дана силаСF{− 5, −1, − 4 } , точки A(

− 2,3,6) и B(1,5, − 3). Оп-

ределить момент силы F относительно точки В.

Решение. Момент силы F , приложенной к точке А относительно точки В, – это вектор, равный векторному произведению вектора пере-

мещения BA = {− 3; − 2; 9} на вектор силы F :

F 0 =					i	j	k	=
					i	j	k
		×		=	− 3 − 2 9
	BA	×	F	=	− 3 − 2 9
					−	5 −1	− 4

Итак, А=19; F0 =17i − 57 j − 7k .

Задачи для самостоятельного решения

1. Найти единичный вектор, перпендикулярный векторам

a = i + j + 2 k и b = 2i + j + k .

2. Найти векторное произведение векторов

a= 2i + 5 j + k и b = i + 2 j − 3k .

3.Вычислить площадь треугольникаИс вершинами A(2, 2, 2); B(4, 0, 3) и C(0,1, 0). ДАОпределить

1. ±

− 3

+ 7 j − k .

2. −17i

(ед.2 ).

+ 5

+13

4. −19i

Вопросы и задания для самопроверки [1,2,3,4,6]

1.Дайте определение векторного произведения векторов.

2.Сформулируйте критерий коллинеарности векторов.

3.Как вычисляют через координаты векторов их векторное произведение?

4.Поясните геометрический смысл векторного произведения.

5.Чему равно векторное произведение i × j ?

<<< < Предыдущая 1 23 / 103 4 5 6 7 8 9 10 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
07.01.202112.38 Mб62488.pdf
#
07.01.202112.4 Mб972489.pdf
#
07.01.2021371.26 Кб4249.pdf
#
07.01.202112.58 Mб92490.pdf
#
07.01.202112.85 Mб142491.pdf
#
07.01.202112.89 Mб122492.pdf
#
07.01.202112.89 Mб212493.pdf
#
07.01.202113.06 Mб192494.pdf
#
07.01.202113.16 Mб402495.pdf
#
07.01.202113.16 Mб192496.pdf
#
07.01.202113.16 Mб222497.pdf