2250

Как видно на рис. 2.9, информация о дефекте может быть выведена на дисплей специального тестера при техническом обслуживании или ремонте машины. Для такого внешнего диагностирования используются различные по назначению и сложности сканеры или тестеры. Простейшие тестеры позволяют вывести из памяти бортового микроконтроллера информацию в виде кода дефекта. Затем эти более подробные сведения можно сопоставить с соответствующими техническими инструкциями. После устранения дефекта можно стереть в памяти блока информацию о дефекте.

Рис.2.9.Техническое диагностирование гидравлического экскаватора 345 BL фирмы Caterpillar с использованием электронной системы «Маэстро» и внешнего (переносного) тестера

Существуют более универсальные тестеры, позволяющие выполнить не только указанные выше операции, но и определить параметры электрических сигналов в различных точках системы при ее функционировании и на основе анализа изменения информативных параметров провести диагностирование машины (агрегата, узла) по параметрам рабочих процессов.

Наиболее совершенные и сложные тестеры с микропроцессорным управлением могут вести диагностирование в автоматизированном режиме. Информация об особенностях конкретной диагностируемой системы, кодах дефектов, методиках диагностирования и способах устранения дефектов, применительно к различным машинам, хранится на жестких или гибких носителях (картриджах-дискетах).

2.4. Кодирование информации

Мгновенное значение квантованного рабочего процесса (см. табл. 2.2) или некоторой квантованной величины может быть представлено числом квантов в некоторой системе счисления или числовым кодом.

Код – это совокупность условных знаков любой природы, образованная по определенному правилу. Число условных знаков, из которых строится кодовое сообщение, называется основанием кода. Сами условные знаки на-

30

зываются символами или буквами кода. Кодовая комбинация, состоящая из п символов, называется кодовым словом, имеющим п разрядов. Методы построения кодового слова как результата счета связаны с системами счисления. Построение любой системы счисления начинается с выбора ее основания – количества цифр (символов), из которых можно получить любое число.

Цифра – это абстрактный символ счета, воспринимаемый и используемый для записи кодов.

Втехнических системах цифры представляются кодами с использованием квантованных носителей информации. Существуют различные системы счисления, но в технике наиболее распространены двоичная и десятичная системы.

Воснову двоичной системы положено два символа (0 и 1). Десятичная система имеет десять символов (от 0 до 9). Двоичная система счисления нашла применение в дискретной технике ввиду широкого распространения элементов с двумя явно выраженными устойчивыми состояниями. Такими элементами, например, являются реле, триггеры и другие устройства, с помощью которых можно легко представлять двоичные символы.

Различают позиционные коды, в которых символу, стоящему на определенной позиции, называемой разрядом, присваивается определенный вес, и непозиционные коды, в которых место символов в разрядах кода может быть произвольным /20/. Примером непозиционного кода является единичный (унитарный) код. Основание кода – единица, вес всех разрядов одинаков и равен единице.

Позиционные коды могут быть представлены многочленами, для которых задается конечное число символов и правило определения числа. Так,

n -разрядное число запишется в виде

N qn = anqn-1 + an-1 qn-2 + … + a2q1 + a1 q0, ( 2.1)

где q – основание системы счисления; a – символ кода, имеющий значения от 0 до q – 1 .

Чем меньше основание, тем длиннее кодовое слово, то есть требуется больше разрядов для представления одного и того же числа.

Так, число 170 в десятичной системе запишется тремя разрядами:

N103 = 1 · 102 + 7 ·101 + 0 · 100 = 170,

а в двоичной системе, где символы принимают только два значения (0 или 1), его можно представить восьмиразрядным кодом в виде полинома от ос-

нования 2 и упрощенно:

N28 = l ·27 + 0 · 26 + l · 25 + 0 ·24 + 1 · 23 + 0 · 22 + 1 · 21 + 0 ·20 = 10101010.

В единичном коде число 170 будет представлено 170 разрядами.

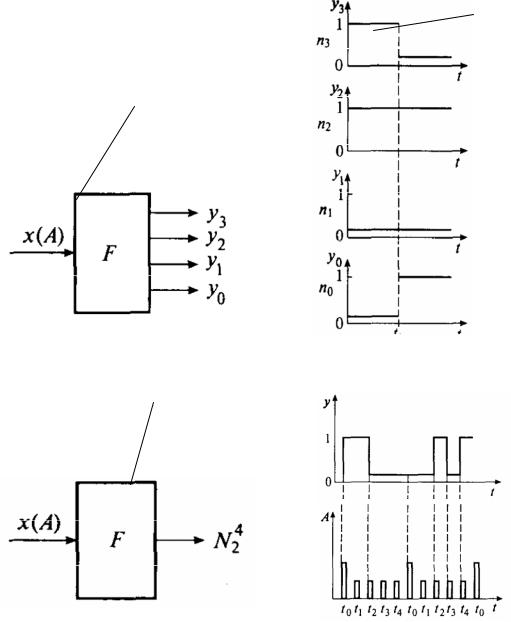
При передаче информации коды могут передаваться параллельно или последовательно. На рис. 2.10 /20/ показан преобразователь F, преобразующий величину х (А) с амплитудной модуляцией в выходную величину

31

t1

у(N24)

t t

а)

у (N24)

б)

Рис. 2.10. Двоичные элементы с параллельным (а) и последовательным (б) выходами и диаграммы их сигналов на выходах

с кодовой модуляцией, представляемой параллельным четырехразрядным двоичным кодом у (N24).

Преобразователь F c последовательным выходом преобразует входную величину х(А) с амплитудной модуляцией в выходную величину N24 с дис- кретно-кодовой модуляцией, представляемой последовательным четырехразрядным кодом. Для параллельного кода y (N24) приведены диаграммы сигналов на выходах, которые являются разрядами двоичного кода и представляются амплитудой величины уi. Они могут принимать два значения: 1 или 0. До момента времени t1 код (N24)1 = 1100,а после t1 код (N24)2 = 0101.

32

Для последовательного кода (N24) на рис. 2.10, а приведены диаграммы сигналов на выходе. Разряды кода появляются на выходе в моменты времени t0, … ,t4, определяемые тактовыми импульсами, а начало кода определяет синхроимпульс, который на диаграмме имеет большую амплитуду.

2.5.Преобразование и передача информации

Кнастоящему времени разработана формальная математическая теория преобразования и передачи информации с помощью дискретноквантованных сигналов. Она исходит из представления об информации как

остепени снятия неопределенности, которую можно установить, например, выбором одного из двух решений. Если появляется сообщение о часто встречающемся событии, вероятность появления которого близка к единице, то такое событие для получателя малоинформативное. Столь же малоинформативные сообщения о событиях, вероятность появления которых близка к нулю.

Поскольку при техническом диагностировании информацию относят к исследуемому объекту, считая ее функцией оценки состояния объекта, увеличение данных о нем означает уменьшение неопределенности. Информация связывается с вероятностью оценки состояния объекта диагностирования, а следовательно, и сэнтропией/7, 11, 35, 39/.

В математической теории связи рассматривается источник сообщений, который в определенной ситуации может создать любое сообщение из множествавозможных.

Энтропия в математической теории связи есть мера неопределенности, которая берется в качестве меры количества информации от данного источника. Чем больше известно о том, какое сообщение будет создано источником, тем меньше неопределенность, энтропия и количество информации. Энтропия – это мера количестваинформации.

Определим, как можно количественно измеритьнеопределенностьприоценке состояния диагностируемого объекта. Понятие неопределенности состояния связано с понятием информации. Определим количество информации, если предположение онеопределенности состояния объекта снято. Предположим, что в начальный момент можно судить о некотором событии, например о том, что

отказал проверяемый элемент с вероятностью p д (вероятность до испытания), а послеиспытания– свероятностьюpп (вероятностьпослеиспытания). Определим количество информации, полученной в результате испытания и вызвавшей такое изменениевероятностей. Пусть

33

Число β может служить мерой информации /11/, показывая, во сколько раз изменилась вероятность при получении информации. Но более удобным является измерение информации не в виде отношения, а в виде приращения. В этом случае мерой информации J является логарифм β , то есть

При этом количество информации не зависит от того, передается ли информативный параметр сразу или по частям.

Действительно, если вероятность отказа некоторого элемента до испытанияβ д = 0,5, а после первого теста в испытании β п = 0,7, то количество

информации, полученной в результате испытания,

J 1 = log 0,7 – log 0,5.

Если после второго теста в испытании β п=1,0, то количество информа-

Вероятность получения такого количества информации равна вероятности того, что откажет именно i-й элемент. В свою очередь, эта вероятность равна коэффициенту отказаβ i.

Коэффициент отказа βi /11/ представляет собой отношение среднего

числа отказов элементов i-го типа за время t к среднему числу отказов объекта за этот же промежуток времени и определяется в случае простейшего потока отказов по формуле

Следовательно, «вклад» i-го элемента в общее количество ожидаемой, информации равен:

Просуммировав «вклады» всех элементов, получим выражение для определения количества ожидаемой информации:

Установим связь между энтропией и информацией. Как уже отмечалось, при получении информации о состоянии объекта диагностирования неопределенность оценки его состояния уменьшается. Чем больше объем полученной информации, тем меньше неопределенность оценки состояния. Если в результате испытания выясняется, какой из элементов объекта отказал, то неопределенность оценки состояния объекта равна нулю. Следовательно, если до получения информации, до определения испытания, энтропия состояния равна Н, а после получения информации о состоянии объекта Н = 0, то

J = H – 0 = H. (2. 7)

Если состояние объекта выясняется в результате проведения ряда проверок (тестов) в одном испытании, то можно говорить об информации, полученной за один или ряд тестов. Так, если до j-го теста энтропия состояния системы Hj -i,а после теста – Hj,то информация, полученная в результате j-го теста,

Таким образом, процесс получения информации при диагностировании является одновременно процессом уменьшения энтропии в оценке состоя-

ния объекта диагностирования /11, 35/. Только там, где есть неопределенность, может быть получена информация. Учитывая соотношения (2.6) и (2.7), выражение для определения энтропии состояния объекта диагностирования можно записать в виде

35

N

H = −∑βi log βi . (2. 9)

i=1

Выражение (2.9) определяет среднюю меру неопределенности состояния объекта или его энтропию. Основанием логарифма в формулах (2.6) и (2.9) может быть любое положительное число, а ≥ 1. На практике целесообразно пользоваться логарифмом при основании 2, что позволяет измерять информациювдвоичнойсистеме/7, 39/:

n

H = −∑ pi log2 pi , (2.10)

i=1

где n – число двоичных символов кода; pi – вероятность того, что будет выбран i-й символ.

Информация измеряется не числом возможных сообщений, а логарифмом этого числа (для двоичных чисел – числом разрядов).

Информация – это объективная мера оценки разнообразия рабочих процессов и состояний объекта диагностирования с учетом влияния внешних условий на объект.

Легко убедиться, что при выборе основания логарифма 2 за единицу измерения энтропии принимается неопределенность состояния простейшей системы (N = 2), имеющей дваравновозможных состояния.

Действительно, на основании формулы (2.9)

Определенная таким образом единица энтропии (бит) называется двоичной единицей и обозначается bit (от английского словосочетания binary digit – двоичное исчисление).

За единицу количества информации принимают такое ее количество, которое получаютпривыбореиздвухравновероятныхвозможностей.

Кодовая комбинация из 8 бит называется байтом.

2.6. Свойства состояний объекта диагностирования

Энтропия состояния объекта диагностирования обладает рядом свойств /11/, оправдывающих ее выбор в качестве характеристики меры неопределенности.

1. Энтропия обращается в нуль, когда одно из состояний объекта диагностирования достоверно, а все другие невозможны.

Действительно, в этом случае все коэффициенты отказа в формуле (2.9) обращаются в нуль, кроме одного, например, β k, который равен единице. Так как log 1 = 0, тоβ k log β k = 0. Применим правило Лопиталя к

36

f (βi ) = logββi . 1/ i

Получим (при β i = 0)

Следовательно, остальные члены также равны нулю, поскольку lim β i log β i = 0 приβ i = 0.

2. Энтропия состояния объекта диагностирования с конечным множеством состояний максимальна, когда эти состояния равновероятны.

Это свойство энтропии состояния объекта диагностирования легко показать для простейшего случая – диагностирование объекта с двумя возможными состояниями (N=2).

Пусть вероятности этих состоянийβ 1 и β 2. Тогда энтропия состояния такого объекта в соответствии с формулой (2.9) равна:

H (N = 2) = −β1 log β1 − β2 log β2 .

Учитывая, чтоβ 1 + β 2 = 1, имеем

H (N = 2) = −β1 log β1 − (1 − β1 )log(1 − β1)

или, переходя к натуральным логарифмам,

H (N = 2) = −loge[β1 ln β1 + (1 − β1 )ln(1 − β1)].

Для определения значения β 1, при котором энтропия состояния объекта диагностирования достигает наибольшего значения, продифференцируем полученное выражение поβ 1 и производную приравняем нулю:

или

ln β1 − ln (1 − β1) = 0 .

Отсюдаβ 1 =1 – β 1. Следовательно, максимум энтропии H (N = 2) достигается при

β 1 = β 2 = 1/2 ,

что и требовалось доказать.

Распространяя полученные результаты на объект диагностирования с N возможными состояниями, можно утверждать, что энтропия такого объекта максимальна, если эти состояния равновероятны:

При этом

37

N

H (N ) = −∑βi log βi < log N , (2.11)

i=1

если хотя бы один из коэффициентов отказа не равен всем остальным. Из неравенства (2.11) следует важный практический вывод: энтропия состояния объекта диагностирования тем меньше, чем больше отли-

чаются друг отдругазначениявероятностейβ i (i =1, N).

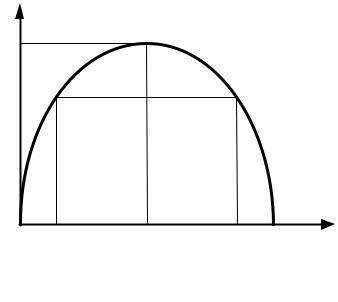
На рис. 2.11 представлена зависимость энтропии состояния объекта диагностирования, состоящего из двух элементов, от величины коэффициентов их отказа.

Рис. 2.11. Зависимость эн-

тропиисостоянияобъекта диагностированияотвеличиныкоэффициентов отказа

Как следует из анализа представленной зависимости, энтропия состояния объекта диагностирования с двумя равновозможными состояниями максимальна и равна одной двоичной единице, энтропия состояния этого же объекта при всех других сочетаниях значенийβ 1 иβ 2 меньшеединицы.

3. Энтропия состояния объекта диагностирования обладает свойством аддитивности, то есть при объединении нескольких независимых объектов ихэнтропиискладываются.

Рассмотрим два независимых элемента А1 и А2,имеющих соответственно N1 и N2 равновероятных состояния. Энтропии состояний элементов А1 и А2 соответственно равны: H (N1) = log N1 и H (N2)=log N2. Объединим эти элементы в один объект. Очевидно, неопределенность состояния объекта будет больше, так как число его возможных состояний равно N1 · N2 (поскольку на каждое состояние элемента А1 приходится N2 состояний элемента А2). Тогда энтропия состояния объекта диагностирования, состоящего из двух элементов,

Н(N1N2) = log N1N2 = log N1 + log N2 = H (N1) + H (N2). (2.12)

Статистическая теория информации разработана для оценки количества и скорости передачи информации, а не для определения содержания сообщения. Одно и то же сообщение от некоторого объекта или системы может

38

по-разному восприниматься приемником информации. Информационная ценность системы диагностирования зависит не от количества заключен-

ной в ней информации (оно бесконечно), а от того, как используется эта информацияпридиагнозеилипрогнозетехническогосостояниямашины.

Различные подходы /20/ к определению ценности (качества) информации предлагают оценивать количество информации и возможность с ее помощью решать поставленную задачу. В семантической (смысловой) теории информации предполагается, что для понимания и использования информации получатель должен обладать определенным запасом знаний. Если назвать имеющиеся у получателя знания о данном объекте диагностирования тезаурусом, то есть неким сводом слов, понятий, названий элементов, связанных смысловыми отношениями, а также характеристик происходящих в них процессов, то количество информации, содержащееся в некотором со-

общении, можно оценить степенью изменения индивидуального тезауруса

под воздействием данного сообщения. Иными словами, количество семантической информации, извлекаемой получателем из поступающих сообщений, зависит от степени подготовленности его тезауруса для восприятия такой информации. Семантическая информация возникает в процессе взаимодействия сообщения с тезаурусом объекта диагностирования.

Контрольные вопросы ко второй главе

1.Что понимается под терминами «информация», «теория информа-

ции?»

2.Что представляет собой процесс измерения величин?

3.Как классифицируют величины (параметры) в технической диагностике?

4.Какие диагностические параметры можно привести в примерах, характеризующих:

–косвенные показатели износа узлов ДВС;

–прямой показатель износа агрегатов трансмиссии машины?

5.Как классифицируют диагностические параметры в зависимости от вида рабочих (энергетических) процессов, а также свойств агрегатов, систем, узлов и деталей машин?

6.Какие диагностические параметры рабочих процессов можно привести в качестве примеров, характеризующих функциональные свойства агрегатов, узлов и систем машин:

–для механических параметров;

–для геометрических параметров;

–для электрических параметров?

39