
- •ВВЕДЕНИЕ
- •1. РАЗРАБОТКА ГРУНТОВ ЗЕМЛЕРОЙНЫМИ МАШИНАМИ
- •1.1. Анализ существующих теорий процесса разработки грунтов землеройными машинами
- •2. МАТЕМАТИЧЕСКАЯ МОДЕЛЬ ПРОЦЕССА ВЗАИМОДЕЙСТВИЯ РАБОЧЕГО ОРГАНА ЗЕМЛЕРОЙНОЙ МАШИНЫ С ГРУНТОМ
- •2.1. Методология исследования. Описание математической модели
- •2.4. Установление закономерности распределения давлений по длине рабочего органа
- •3. АДАПТАЦИЯ МАТЕМАТИЧЕСКОЙ МОДЕЛИ К РЕАЛЬНЫМ ПРОЦЕССАМ РАЗРАБОТКИ МЕРЗЛЫХ ГРУНТОВ
- •3.1. Построение эпюры распределения напряжений по длине рабочего органа рыхлителя на основе экспериментальных данных
- •3.2. Определение значений коэффициентов, входящих в математическую модель, для ее корреляции
- •3.3. Обоснование выбора реологической модели мерзлого грунта
- •3.3.1. Определение величины сжимаемости немерзлых грунтов
- •4. ОПТИМИЗАЦИЯ ПАРАМЕТРОВ РАБОЧЕГО ОРГАНА
- •4.1. Определение и анализ конфигурации оптимальной контактной поверхности рабочего органа
- •4.1.1. Определение конфигурации оптимального продольного профиля рабочего органа
- •4.4. Инвестиционная привлекательность исследований
- •ЗАКЛЮЧЕНИЕ
- •БИБЛИОГРАФИЧЕСКИЙ СПИСОК

4.1. Определение и анализ конфигурации оптимальной контактной поверхности рабочего органа
4.1.1. Определение конфигурации оптимального продольного профиля рабочего органа
С |
|
|
Алгоритм: |
|
|
1. |
Запишем формулу для расчета горизонтальной составляющей |
|
усилия рыхлен я при про звольном цилиндрическом профиле наконечни- |
||
ка. |
|
|
относительное |
удельное сопротивление рыхлению k0 . |
|
2. |
Определяем |
|
3. |
Опт мальная форма наконечника находится при условии ограни- |
|
чения его дл ны. |
|
|
|
|
|
|
4. Задача решается с помощью уравнения Эйлера - Лагранжа. |
|
|||||
бА |
|
|||||
Задача решается для продольного профиля наконечника зуба рыхли- |
||||||
теля. Рассматр вается прямолинейный продольный профиль (рис. 4.4). |
||||||
Д |
|
|||||
|
|
|
И |
|||
Рис. 4.4. Расчетная схема прямолинейного |
|
|||||
продольного профиля наконечника |
|
|||||
Формула для расчета нормального давления на плоский наконечник |
||||||
имеет вид |
|
|
|
|
|
|
Y |
|
|
X |
|
|
|
P p0 Q |
|
|
P |
|
, |
(4.1) |
|
L |
|||||
l |
|
|
|
|
||
97

где p0 – величина нормального давления в средней верхней точке нако-
нечника; Q |
Y |
|
, P |
X |
|
– функции, учитывающие изменение давления по |
||
l |
L |
|||||||
|
|
|
|
|
||||
ширине и длине наконечника соответственно; |
X , Y – абсолютные коор- |
|||||||
динаты произвольной |
точки наконечника в |
системе координат X Y Z |
||||||
С |
– по ширине наконечника); L – длина нако- |
(X направлена по длине, Y |
нечника; l – полуширина наконечника.
делаем допущение, что закон распределения нормального давления
по длине наконечн ка такой же, как и по глубине рыхления. |
|
||||||
Из р с. 4.5 следует, что |
|
|
|
|
|
|
|
точки |
|
X |
|
x |
x, |
(4.2) |
|
|
|
|
|
|
|||
|
|
|
L h |
|
|||
где x , x – абсолютная относительная вертикальная координаты произ- |
|||||||
вольной |
наконечн ка. |
|
|
|
|
|
|
|
глуб |
|
|||||
Так м образом, для прямолинейного профиля наконечника относи- |
|||||||
тельная коорд ната x является одновременно относительной длиной и от- |
|||||||
носительной |
ной наконечника. |
|
|||||
Рассмотр м схему сил, действующих на элементарную площадку |
|||||||
|
А |
|
|||||
наконечника, имеющего криволинейный профиль (см. рис. 4.5). |
|
||||||
|
|
Д |
|
||||
|
|
|
|
|
|
И |
|
Рис. 4.5. Схема сил, действующих на элементарную площадку рабочего органа криволинейного профиля
98
Горизонтальная сила, действующая на элементарную площадку наконечника криволинейного профиля dS , в системе координат x y z равна
d Eг Pcosα F sinα dS, |
(4.3) |
где P, F – нормальное и тангенциальное давления на площадке dS; α – те- |
|
С |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
кущее значение угла наклона к касательной в рассматриваемой точке кри- |
||||||||||||||||||||||
волинейного профиля. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Из формулы (4.1) с учетом выражения (4.2) имеем |
|
|||||||||||||||||||||
где |
|
|
|
P |
p0 Q y P x , |
|
|
|
(4.4) |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
y' |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
y |
. |
|
|
|
|
|
|
|
(4.5) |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
l |
|
|
|
|
|
|
|
||
Введем также относ тельную координату по горизонтали при помо- |
||||||||||||||||||||||
бА |
|
|
|
|||||||||||||||||||
щи соотношен я |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
и z |
z' |
. |
|
|
|
|
|
(4.6) |
||||||||||||||
l |
|
|
|
|
|
|||||||||||||||||
Уч тывая, что |
|
|
|
|
|
|
|
T P f , |
|
|
|
|
|
|
(4.7) |
|||||||
|
dS |
dx |
dy |
|
|
d x h d l y |
|
h l dx dy |
, |
(4.8) |
||||||||||||
cos α |
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
cos α |
|
|
|
|
cos α |
|
|||||
формула (4.3) принимает вид |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
dEг P h l (1 f tgα) dxdy. |
(4.9) |
||||||||||||||||||
|
|
|
|
|
|
Д |
|
|||||||||||||||
С учетом выражений (4.2) и (4.6) |
|
|
|
|
|
|
|
|||||||||||||||
|
|
tg |
d z |
|
d h z |
dz . |
|
|
|
(4.10) |
||||||||||||
|
|
|
|
|
dx' |
|
|
|
|
d h x |
dx |
|
|
|
|
|||||||
Суммарное горизонтальное усилие находим, проинтегрировав выра- |
||||||||||||||||||||||
жение (4.9) с учетом (4.4) и (4.10): |
|
|
|
|
|
|
|
|
|
|
И |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
1 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
1 |
|
|
|
Eг p0 Q(y) P(x) l h (1 |
f z') dxdy p0 |
l h Q(y) dy P(x) (1 f z')dx |
||||||||||||||||||||
0 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
0 |
|
|
|||
1 |
|
|
|
f z')dx. |
|
|
|
|
|
|
(4.11) |
|||||||||||
p0 l h ky P(x) (1 |
|
|
|
|
|
|
||||||||||||||||
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Откуда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
E г |
|
|
|
|
k y |
1 |
|
|
|
|
|
|
z ' )dx , |
(4.12) |
|||||||
|
|
|
|
k 0 |
|
|
|
|
|
|
|
P ( x ) (1 f |
||||||||||
|
|
|
|
|
2 |
|
|
|||||||||||||||
|
2 l h p 0 |
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|||||||
где ky – коэффициент, учитывающий степень неравномерности распреде-
ления давления грунта по ширине наконечника; 2l – ширина наконечника.
99

Левая часть уравнения (4.12) представляет собой отношение удельного сопротивления рыхлению к минимальному нормальному давлению в верхней части рабочего органа p0 (относительное удельное сопротивление рыхлению):
С |
|
|
|
|
|
|
|
ky |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
k0 |
|
|
|
P(x) (1 f z')dx. |
(4.13) |
||||||||||||||||||||||
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
2 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
Задаем дополнительное ограничение: длина профиля наконечника |
|||||||||||||||||||||||||||
ограничена. Тогда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
и |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
L |
1 z'2 |
hdx . |
(4.14) |
|||||||||||||||||||||
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
Откуда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
L |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 z'2 dx. |
(4.15) |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
h |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
С учетом огран чен я (4.15) оптимальная форма профиля наконеч- |
|||||||||||||||||||||||||||
ника наход тся з решен я уравнения Эйлера-Лагранжа |
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
F' (x,z,z') |
d |
F' |
(x,z,z') 0, |
(4.16) |
||||||||||||||||||
|
|
|
|
|
|
|
dx |
||||||||||||||||||||||
где |
|
|
|
|
|
z |
|
|
|
|
|
|
|
|
z' |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
ky P(x) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
F(x,z,z') |
(1 f z') λ 1 z'2 , |
(4.17) |
|||||||||||||||||||||||||
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
где λ – неопределенный множитель Лагранжа. |
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
2 |
|
|
|
|
|
|
|
|
|
|
Д |
||||||||||||||||
|
|
Последнее слагаемое в формуле (4.17) учитывает ограничение длины |
|||||||||||||||||||||||||||
рабочего органаб. Следует отметитьА, что задача нахождения оптимального |
|||||||||||||||||||||||||||||
продольного профиля наконечника без ограничения (глобального экстре- |
|||||||||||||||||||||||||||||
мума) решения не имеет. Если в выражении (4.17) положить λ 0, то име- |
|||||||||||||||||||||||||||||
ем: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
И |
||||||
F(x,z,z') ky P(x) (1 f z'). Откуда F' (x,z,z') 0. Следовательно, |
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z |
|
|
|
|
|
|
|
взяв частную производную в выражении F(x,z,z') |
ky P(x) |
(1 f z') по |
|||||||||||||||||||||||||||
|
|
|
|
|
|
ky |
P(x) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
||||||
|
, |
|
|
f . Взяв производную по x в последнем |
|||||||||||||||||||||||||
|
|
|
|
|
|||||||||||||||||||||||||
z |
имеем Fz (x,z,z') |
|
|
2 |
|
|
|||||||||||||||||||||||
|
|
|
d |
|
|
|
|
|
|
|
|
ky P x |
|
|
|
|
|
|
|||||||||||
|
|
|
F' |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
выражении, имеем |
|
|
(x,z,z') |
|
|
|
|
|
|
|
|
f |
. С учетом вышеизложен- |
||||||||||||||||
dx |
2 |
|
|
||||||||||||||||||||||||||
|
|
|
|
z' |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ky P x |
|
|||||||||
ного уравнение (4.16) принимает вид |
|
|
|
|
|
|
f 0. Полученное урав- |
||||||||||||||||||||||
|
2 |
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
нение не может быть решено относительно переменной z и тождественно
100

не равно нулю, что свидетельствует о некорректности поставленной задачи поиска глобального экстремума.
При λ ≠0 и
|
|
|
|
|
|
|
|
F' |
(x,z,z') 0 |
|
|
(4.18) |
||||||||
|
|
|
|
|
|
|
|
z |
|
|
|
|
|
|
|
|
|
|
|
|
уравнение Эйлера-Лагранжа (4.16) принимает вид: |
|
|||||||||||||||||||
|
|
|
|
|
|
d |
F' |
(x,z,z') 0. |
|
|
(4.19) |
|||||||||
|
|
|
|
|
|
|
|
|
||||||||||||
|
ледовательно, при |
|
|
dx |
z' |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
Fz'(x,z,z') с const |
|
|
(4.20) |
|||||||||||||||
из выражен я (4.17) находим |
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
профиля |
|
|
|
|
|
|
|
|
z' |
|
|
|
|||||||
|
|
|
' |
ky |
P( x) |
|
|
|
|
|
|
|
|
|
||||||
СF ( x,z,z' ) |
|
|
|
|
f |
|
|
|
|
|
c const. |
(4.21) |
||||||||
|
|
|
z' |
|
2 |
|
|
|
|
|
|
|
1 z'2 |
|
|
|
||||
|
Анал з руя формулу (4.21) можно заметить, что форма оптимально- |
|||||||||||||||||||
го |
|
|
бА |
|
||||||||||||||||
|
|
наконечн ка зависит от типа грунта. |
|
|
|
|||||||||||||||
|
Обознач м вел ч ну |
|
|
|
|
ky |
|
P( x) |
|
f |
|
|
|
|||||||
|
Тогда (4.21) примет вид |
|
|
|
|
|
|
2 |
|
|
( x). |
(4.22) |
||||||||
|
|
|
|
|
( x) |
|
|
z' |
|
c const. |
(4.23) |
|||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
1 z'2 |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
Постоянная c может быть найдена из условия, что значение угла ре- |
|||||||||||||||||||
зания α p |
известно. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Тогда |
|
|
|
|
|
z' ctgαp . |
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
(4.24) |
||||||||||
|
Подставляя (4.24) в (4.23), получим |
|
|
И |
||||||||||||||||
|
|
|
c θ(1) ctgα |
|
|
|
|
|
|
|||||||||||
|
|
|
|
/ 1 сtg2α |
θ(1) cosα |
(4.25) |
||||||||||||||
|
|
|
|
|
|
|
|
Дp р p . |
||||||||||||
|
Решаем уравнение (4.24) относительно переменной z : |
|
||||||||||||||||||
|
|
|
|
z' z x |
|
|
c ( x) |
|
|
|
||||||||||
|
|
|
|
|
1 c ( x) 2 . |
(4.26) |
||||||||||||||
|
Уравнение продольного профиля найдется в результате интегриро- |
|||||||||||||||||||
вания выражения (4.26): |
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
c ( x) |
|
|
|
||||||
|
|
|
|
|
z |
|
|
|
|
|
|
|
|
|
|
|
dx. |
(4.27) |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
0 1 c ( x) 2 |
|
|
|
|||||||||||
101

В подынтегральное выражение входит неопределенный постоянный множитель Лагранжа λ. Интегрирование его в квадратурах является сомнительным.
Дальнейшее решение задачи представляется следующим.
Задаваясь λ, вычисляется значение функции z z(x) в численном виде, исходя из интеграла (4.27) с учетом формул (4.22) и (4.25).
СибАДИ |
||||
Далее находим значение относительной длины наконечника |
L |
, вы- |
||
|
|
|
h |
|
числяя интеграл (4.15), которое для выбранного значения λ = 200 состав- |
||||
ляет 2,31. |
|
|
||
тро м граф к опт мального продольного профиля наконечника в |
||||
относительных ед н цах для значения относительной длины |
L |
, |
равного |
|
|
h |
|
|
|
2,31 (рис. 4.6). |
|
|
||
Рис. 4.6. Оптимальный продольный профиль рабочего органа
Из анализа графика следует, что оптимальный продольный профиль наконечника имеет криволинейный характер. При увеличении значения λ форма профиля приближается к прямой.
102

Задаваясь различными значениями λ в интервале [200; 2000], нахо-
дим значения относительной длины L по формуле (4.15) и удельного со- h
противления рыхлению k0 из выражения (4.13).
По полученным векторам λ и k0, а также L и k0 строим графики за- h
СибАДИвисимостей k0 = f (λ) k0 f L (рис. 4.7 и 4.8).
h
Рис. 4.7. Зависимость относительного удельного сопротивления рыхлению от множителя Лагранжа
103

Рис. 4.8. Зависимость относительного удельного сопротивления рыхлению от относительной длины оптимальной формы наконечника
Из анализа графиков следует, что относительное удельное сопротивление рыхлению уменьшается с уменьшением относительной длины наконечника, а также при увеличении неопределенного множителя Лагран-
жа. |
|
|
|
Проанализируем зависимости (4.22) – (4.27). |
|
||
При λ → ∞ выражение (4.22) принимает вид |
|
||
|
( x) 0. |
|
(4.28) |
Из выражения (4.25) с учетом формулы (4.28) имеем |
|
||
|
c cosα |
|
|
СибАДp ; И(4.29) |
|||
z' |
cos α p |
ctg α p . |
(4.30) |
|
|||
|
|||
1 cos 2 α p |
|
|
|
Уравнение оптимального продольного профиля наконечника при |
|||
→ ∞ примет вид |
|
|
|
|
z x ctg |
α p . |
(4.31) |
104

Выражение (4.31) описывает прямолинейный продольный профиль наконечника, установленный под углом αp к горизонту. На рис. 4.8 нача-
ло координат (при L = 2) соответствует параметрам оптимальной прямо-
h
линейной формы наконечника, так как удельное сопротивление рыхлению при этом минимально. Таким образом, приходим к выводу, что оптимальный продольный профиль наконечника для любых типов грунтов должен быть прямолинейным.
4.1.2. Анал т ческое решение задачи об оптимальной форме продольного проф ля лобовой поверхности рабочего органа
При решен научных задач необходимо стремиться к получению аналитического решен я, хотя ы приближенного, поскольку оно содержит более емкую наглядную информацию, легче анализируется.
Решен е задачи об оптимальной форме продольного профиля опре-
деляется |
|
нтегралами (4.14) и (4.27). Как видно, в выражение (4.27) вхо- |
|||||||||||||||||||||
дит разность с θ x . |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Из выражений (4.22) и (4.25) имеем |
|
|
|
|
|
|
|
|
|||||||||||||||
c θ x θ 1 cosαр |
θ x |
ky P 1 f |
|
cosαp |
k y P x f |
|
|||||||||||||||||
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 λ |
|
|
|
|
|
|
2 λ |
(4.32) |
|
|
ky f |
P 1 P x cosαp , |
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
2 λ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
где |
|
|
|
|
|
|
|
|
|
P x 1 2 a |
a |
|
|
e |
a x |
2 |
(4.33) |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
3 |
x, |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
3 |
|
|
|
e a3 . |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
P 1 1 2 a |
2 |
a |
|
(4.34) |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
||||
Подставляя формулы (4.33) (4.34) в выражение (4.32), получим |
|||||||||||||||||||||||
c θ x |
|
k y f |
|
|
1 2 a2 |
a3 e a 3 1 2 a2 a |
|
3 x e a 3 x2 cos α p |
|
||||||||||||||
|
2 λ |
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(4.35) |
||
|
k y f |
e a 3 x e a 3 x2 |
2 a2 a3 cos α p cos α p T , |
||||||||||||||||||||
|
|||||||||||||||||||||||
|
|
||||||||||||||||||||||
|
|
2 λ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
СибАДИ |
|||||||||||||||||||||||
где |
|
|
|
|
T k |
y |
f a |
a |
e a3 x e a3 x2 , |
|
(4.36) |
||||||||||||
|
|
|
|
|
|
|
|
2 |
|
3 |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 . |
|
|
|
(4.37) |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
λ |
|
|
|
|
|||
При больших значениях λ значения Ψ согласно выражению (4.37) весьма малы.
105

Подставляя выражение (4.37) в уравнение (4.26), получим
cosαp T |
|
z |
|
1 cosαp T ψ 2 . |
(4.38) |
Для нахождения интервала изменения значений λ рассуждаем следующим образом. Из выражения (4.38) нетрудно видеть, что подкоренное
выражение знаменателя должно быть больше нуля: |
|
|
|
|
|
|
|
|
|||||||||||||||||||||
СибАД2a И |
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
1 |
cos α p T |
2 |
0 . |
|
|
|
|
(4.39) |
||||||||||||||
Откуда |
|
|
|
|
|
cosα p T 2 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
1. |
|
|
|
|
|
|
|
(4.40) |
||||||||||||||
Поскольку вел ч ны T и Ψ положительные, то |
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
cos α p T |
|
0 . |
|
|
|
|
|
|
|
(4.41) |
||||||||||||
Выражен е (4.40) может |
ыть записано в виде |
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
cos |
α p |
T |
1 . |
|
|
|
|
|
(4.42) |
||||||||||||
учетом неравенства (4.41) имеем |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
cos α p |
T 1. |
|
|
|
|
|
|
|
(4.43) |
|||||||||||||
Полученное неравенство имеет два решения при определенных зна- |
|||||||||||||||||||||||||||||
чениях Tmax и Tmin. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Можно записать |
|
|
|
|
cos α p T max |
1. |
|
|
|
|
|
|
|
(4.44) |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
Чтобы найти Tmax, возьмем производную из выражения (4.36) |
|||||||||||||||||||||||||||||
|
dT |
k y f a2 a3 e a3 x2 |
1 2a3 x2 0. |
(4.45) |
|||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||
|
d x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Откуда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
. |
|
|
|
|
|
|
|
(4.46) |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2a3 |
|
|
|
|
|
|
|
|
|
||||
Подставляя значение x в выражение (4.36), получим значение Tmin. |
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
2 |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
3 |
|
|
|
||||||||
T |
|
|
k |
y |
f a a |
e a3 |
|
|
|
|
e |
|
2a3 |
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
min |
|
|
2 3 |
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(4.47) |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
e a3 |
|
1 |
|
|
|
|
|
|
|
0,07 k |
|
|
|
|
|
|||||||
k |
y |
f a a |
|
|
|
|
e |
2 |
y |
f a a . |
|||||||||||||||||||
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
2 3 |
|
|
|
|
2a3 |
|
|
|
|
|
|
|
|
|
|
|
2 3 |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x =0 получим |
|||
С учетом формулы (4.46) из выражения (4.47) при |
|
|
|||||||||||||||||||||||||||
значение Tmax |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
106

T |
|
k |
y |
f a |
2 |
a |
3 |
e a3 0,37 k |
y |
f a |
2 |
a |
3 |
. |
(4.48) |
||
max |
|
|
|
|
|
|
|
|
|
|
|||||||
Подставляя полученное значение (4.48) в выражение (4.44), с учетом |
|||||||||||||||||
формулы (4.37) получим |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
cos |
α |
p |
0,37 k |
|
y f a2 a3 |
|
1 . |
|
|
|
|
(4.49) |
|||||
|
λ |
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Откуда находим, что
СибАДИв ряд (4.51) |
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
λ 186 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(4.50) |
||||||||||||
Дальнейшее решение задачи следующее. Разложим правую часть по- |
||||||||||||||||||||||||||||||||||||||||||||||||||
лученного уравнен я в ряд Тейлора по малому параметру Ψ: |
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
z x |
|
z 0 |
z 0 ψ |
|
... . |
|
|
|
(4.51) |
|||||||||||||||||||||||||||||||
Значен е z 0 получим из уравнения (4.51), полагая в нем ψ 0: |
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
z |
|
|
|
|
|
|
|
cos αp T 0 |
|
|
|
|
|
|
ctg αp . |
|
|
|
(4.52) |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 cos |
|
αp |
|
T 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
Чтобы получ ть значение z 0 |
|
в ряде (4.51), прологарифмируем |
||||||||||||||||||||||||||||||||||||||||||||||||
выражен е (4.38) |
прод фференцируем полученное уравнение: |
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
ln z ln cosαp T ψ |
1 |
ln 1 cosαp T ψ 2 , |
(4.53) |
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
T ψ T |
|
|||||||||||
|
|
z |
|
|
|
|
T |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
2 cos |
|
|
α p |
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
z |
cos |
α p |
T ψ |
|
2 |
|
|
1 |
|
cos |
|
|
α p |
|
T ψ 2 |
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
T |
|
|
|
|
|
|
|
|
|
|
cos |
|
α p |
|
T ψ T |
|
|
. |
|
|
|
|
|
|
(4.54) |
||||||||||||||||||
|
|
cos α p |
T ψ |
1 |
|
|
cos |
α p T ψ 2 |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
Положим в выражении (4.54) ψ 0. Тогда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
z 0 |
T |
|
T cosαp |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
cos αp |
|
|
|
|
|
|
|
T |
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
(4.55) |
||
|
z 0 |
|
|
|
|
1 cos αp |
|
T |
|
|
|
|
|
|
|
|
|
|
2 |
αp |
|
|
cos αp sin |
2 |
||||||||||||||||||||||||||
|
|
|
cos αp |
|
|
|
|
|
|
cos αp |
|
|
sin |
|
|
|
|
αp |
|
|||||||||||||||||||||||||||||||
Откуда с учетом (4.52) находим |
|
|
|
|
T |
|
|
|
|
|
|
|
|
|
|
|
T |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
z 0 z 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
(4.56) |
|||||||||||||||||||
|
|
|
|
|
|
|
cos αp sin |
2 |
αp |
|
|
|
3 |
αp |
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
sin |
|
|
|
|
|
|
|
||||||||||||||||||
Подставим |
значения |
|
|
|
0 |
|
|
z |
|
0 |
из |
|
формул |
|
(4.52) и |
(4.56) |
||||||||||||||||||||||||||||||||||
|
|
z |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
z |
|
x ctgαp |
|
|
|
|
|
|
|
T |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
sin3αp |
ψ. |
|
|
|
|
|
|
|
|
|
(4.57) |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
Учитывая выражения (4.56) и (4.57), находим |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
z x ctg αp |
|
|
|
|
k |
|
f |
|
|
e a3 x e a3 x |
2 |
a2 |
a3 . |
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
(4.58) |
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
3 |
αp |
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
sin |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
λ |
|
||||||||||
107

Интеграл полученного выражения (4.58) представляет собой приближенное уравнение оптимального продольного профиля наконечника:
z x |
x |
|
k |
y |
f a |
2 |
a |
3 |
|
e a3 |
|
|
|
x |
2 |
|
1 |
|
|
|
|||||
ctg |
α p |
|
|
|
|
|
|
|
x e a3 |
|
|
dx |
|
||||||||||||
|
sin |
3 |
α p |
|
|
|
|
|
|
||||||||||||||||
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ctg α p |
x |
k y |
f a2 |
|
2 e |
a |
3 a3 |
x e |
a |
3 |
x |
2 |
|
x |
|
|
(4.59) |
||||||||
|
|
|
|||||||||||||||||||||||
2 λ sin |
3 |
α p |
|
|
|
|
|
|
|
|
|||||||||||||||
СибАДИ |
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
x ctg |
α p |
k y |
f a2 |
|
2 e |
a |
3 a3 |
x e |
a |
3 |
x |
2 |
1 . |
|
|
||||||||||
2 λ sin 3 α p |
|
|
|
|
|
|
|
|
|||||||||||||||||
На р с. 4.9 представлены графики зависимостей оптимального продольного проф ля наконечника, вычисленные численным методом согласно интегралу (4.27) (сплошная линия) и по приближенной формуле
(4.58) (штр ховая л н я) при λ = 400.
Рис. 4.9. Графики оптимальных профилей, вычисленные численным аналитическим методами
Из графиков видно, что приближенное аналитическое решение незначительно отклоняется от точного численного решения. Это отклонение будет тем меньше, чем больше значение λ.
При λ→∞получим
z x ctg αp . |
(4.60) |
108

Полученное выражение совпадает с полученным выражением (4.31). Чтобы найти значение неопределенного множителя Лагранжа λ, рас-
смотрим интеграл (4.15).
|
|
|
|
|
cos α T ψ 2 |
|
1 |
|
. (4.61) |
χ |
1 z |
2 |
|
1 |
|
||||
|
1 cos αp T ψ 2 |
1 cos αp T ψ |
2 |
Разложим правую часть полученного уравнения в ряд Тейлора по
СибАДИ1 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
параметру Ψ: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
χ χ |
|
0 |
χ 0 ψ ... |
|
|
. |
|
|
|
(4.62) |
||||||||||||||||||||||||||||
Полож в ψ 0, |
|
|
|
|
з выражения (4.62) находим |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
χ 0 |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 cos 2 αp |
|
|
|
sin αp . |
|
|
|
|
|
|
(4.63) |
|||||||||||||||||||||
Чтобы найти χ |
′( |
) |
, |
продифференцируем функцию (4.61) |
по пара- |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
0 |
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
метру Ψ: |
|
|
|
|
|
1 сos αp T ψ 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
χ ψ |
1 |
|
3 |
2 сos αp T ψ T |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
2 |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(4.64) |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
1 сos αp T ψ 2 |
2 |
сos αp T ψ T . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
Положим в выражении (4.64) ψ 0. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
Тогда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
χ ψ |
|
1 cos2 αp |
|
|
3 |
cosαp |
T T cosα3 |
p . |
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
2 |
(4.65) |
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
sin |
|
|
|
αp |
|
|
||||
учетом вышеизложенного ряд (4.62) представлен в виде |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
χ |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
T cos α p |
|
ψ |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
sin α p |
|
|
|
|
sin 3 α p |
|
|
|
|
|
sin |
|
α p |
|
|
|
|
|
|
|
|
|
|
(4.66) |
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
e |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
cos α p |
|
k y |
f a2 |
|
a3 |
a |
|
|
|
x e |
|
a |
|
x |
2 |
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
sin |
|
|
|
3 |
α p |
|
|
|
|
|
|
|
|
λ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
Интеграл(4.15)сучетомвыражения(4.66)принимает следующийвид: |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
L |
|
1 |
1 |
|
|
|
|
cosαp |
|
k y f a2 |
a3 |
|
|
|
|
a |
|
|
|
|
|
|
|
a |
|
x2 |
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
e |
|
3 |
|
x |
e |
|
|
|
3 |
|
|
|
|
dx |
||||||||||||||||||||
|
h |
sinα |
|
sin |
3 α |
p |
|
|
λ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
0 |
|
|
|
|
|
|
|
|
p |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
cosαp |
|
|
k y |
f a2 |
|
2 e |
a |
3 |
a3 x e |
a |
3 |
x2 |
|
|
(4.67) |
||||||||||||||||||||||||||||||||||||||||
sinαp |
|
|
sin 3 αp |
|
|
|
|
|
2 λ |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
||
|
|
1 |
|
|
|
|
|
|
|
cosαp |
|
|
k y |
f a2 |
2 a3 |
|
e |
|
a |
3 |
e |
a |
3 1. |
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
sinαp |
|
|
sin 3 αp |
|
|
|
|
|
|
2 λ |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
109

Откуда находим |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
L |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
k y f a2 |
|
|
|
h |
|
|
|
|
|
|
|
|
|
|
sin αp |
|
||||
|
2 λ sin 3 αp |
2 a3 |
e a 3 |
e a 3 |
1 сos αp |
. (4.68) |
||||
|
|
|||||||||
Нетрудно видеть, что числитель полученного выражения представляет
СибАДИ |
||||||||||
разностьдлинкриволинейногоипрямолинейногонаконечников(рис.4.10). |
||||||||||
ледовательно, можно утверждать, |
|
|
|
|
||||||
что неопределенный множитель Ла- |
|
|
|
|
||||||
гранжа λ есть вел ч на, обратно |
|
|
|
|
||||||
пропорц ональная |
разности |
|
длин |
|
|
|
|
|||
криволинейного |
прямолинейного |
|
|
|
|
|||||
продольных проф лей наконечника. |
|
|
|
|
||||||
Подставляя выражен е (4.68) в |
|
|
|
|
||||||
уравнен е (4.31), окончательно по- |
|
|
|
|
||||||
лучим пр бл женное уравнение оп- |
|
|
|
|
||||||
тимального продольного |
|
профиля |
|
|
|
|
||||
наконечн ка: |
|
|
|
|
|
|
|
Рис. 4.10. Расчетная схема |
||
|
|
|
|
L |
|
1 |
|
|
|
2 |
|
|
|
|
|
|
|
|
2 e a3 a |
3 x e a3 x |
1 |
|
|
|
|
h |
|
|
|
|
|
|
z x x ctg αp |
|
|
|
sin αp |
1 сos αp |
. (4.69) |
||||
|
|
2 a3 |
e a 3 e a 3 |
|||||||
В полученной формуле первое слагаемое представляет собой уравнение прямолинейного продольного профиля – формула (4.31), а второе слагаемое – поправку, учитывающую разность длин криволинейного и прямолинейного продольных профилей наконечника.
Необходимо отметить, что в полученную зависимость (4.69) не входят ни коэффициент трения f, ни коэффициент ky, учитывающий ширину профиля наконечника.
4.2. Определение анализ конфигурации оптимальной лобовой поверхности рабочего органа
В процессе рыхления статическими рыхлителями происходит отделение грунта от массива и разрыхление до степени, обеспечивающей его дальнейшее транспортирование. После прохода рыхлителя в грунте образуется прорезь трапециевидной формы, в которой выделяют три зоны: вдавливания, сжатия и развала грунта. Геометрия рабочего органа влияет на величину скола грунта и изменение удельного сопротивления резанию
110
в зонах разрушения. Например, известно, что при одинаковых по площади сечениях стружек Fс потребуются меньшие усилия для резания грунта стружкой большей ширины l и меньшей глубины h.
В зонах вдавливания и сжатия происходит блокированное резание грунта. В этих зонах происходит сжатие грунта перед отделением от массива и его вдавливание в дно и боковые стенки прорези. Размер зоны вдавливания грунта в процессе рыхления не изменяется, однако увеличи-
СибАДИвается по мере изнашивания наконечника.
В зоне сжат я в результате увеличения давления на грунт происходит отделен е крупных элементов массива грунта. Для отделения мерзлого грунта от масс ва необходимо создать в грунте давления, превосходящие по вел ч не предельное значение напряжения сжатия грунта [σсж] . В этом случае необход мо о еспечить высокие прочностные свойства рабочего органа.
После скола крупный элемент перемещается по поверхности рабочего органа вверх в сторону, а сопротивление рыхлению резко уменьшается. При дальнейшем дв жении рыхлителя, до образования последующего крупного элемента, от массива откалываются более мелкие элементы грунта. Затем сопрот вление вновь достигает наибольшего значения, и происходит скалывание следующего крупного элемента грунта.
Выкалывание элементов стружки отражается в динамограммах, на которых видно, что к моменту скола усилие достигает своего максимального значения, а сразу после скалывания – резко уменьшается. Затем усилие возрастает при сжатии следующего элемента стружки. Частота возникновения максимальной нагрузки на рабочий орган рыхлителя зависит от физико-механических свойств грунта, глубины, скорости рыхления и геометрических параметров рабочего органа.
Раздробленные мелкие элементы массива будут составлять зону развала грунта. Можно считать, что в этой зоне осуществляется свободное резание грунта.
Величина усилия рыхления грунта в трех зонах различна. При свободном резании усилие рыхления на 45−50% меньше, чем при блокированном. Следовательно, свободное рыхление обладает меньшей энергоемкостью, чем блокированное.
Таким образом, оптимальные геометрические параметры наконечников должны быть такими, чтобы большая по площади часть грунта находилась в зоне свободного рыхления. Кроме этого, необходимо, чтобы та часть грунта, которая находится в зонах вдавливания и сжатия, разрушалась как можно более интенсивно под действием приложенного к рабочему органу усилия рыхления. При этом усилие рыхления по величине
111
должно быть минимальным, но достаточным для разрушения грунта. Это приведет к полной загрузке рыхлителя и минимизации излишков энергоемкости на процесс рыхления мерзлого грунта. Оптимальным будем считать такой поперечный профиль (лобовую поверхность), при котором значение силы сопротивления резанию на рабочий орган будет минимально при постоянной площади его сечения. При минимуме сопротивления ре-
занию на рабочем органе будет снижен его износ. Это в конечном итоге |
|
СибАДИ |
|
приведет к увеличению производительности и снижению энергоемкости |
|
разработки грунта. |
|
Предполож м, что нормальное давление на рабочий орган при его |
|
переменной ш р не определяется выражением (3.67): |
|
P p0 Q y P x , |
(4.70) |
где p0 – вел ч на нормального давления в средней верхней точке рабочего органа; Q y , P x – функции, учитывающие изменение давления по ширине дл не ра очего органа соответственно.
|
|
|
|
|
X |
a3 |
|
X |
2 |
|
||||
|
|
|
|
|
|
|
|
|||||||
P x 1 2 a |
|
a |
|
|
|
|
e |
|
|
L |
, |
(4.71) |
||
|
|
|
|
|
||||||||||
|
2 |
3 |
|
L |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Y 2 |
|
|
|
|
|
|||||
|
|
1 a |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|||||
Q y |
|
|
l |
|
, |
|
|
|
(4.72) |
|||||
|
Y 2 2 |
|
|
|
||||||||||
|
|
|
|
|
|
|
||||||||
|
|
1 b |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
l |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
где L, l – соответственно длина |
полуширина рабочего органа; X, Y – аб- |
|||||||||||||
солютные координаты произвольной точки поверхности рабочего органа; x, y – относительные координаты точек поверхности рабочего органа.
Нормальное усилие, приходящееся на лобовую поверхность рабочего органа (рис. 4.11), определяется выражением
N PdS p0 |
P X Q Y d X dY , |
(4.73) |
|||
S |
S |
|
|
||
где S – площадь лобовой поверхности наконечника. |
|
||||
Положим |
Y |
|
|
||
|
y; |
(4.74) |
|||
|
Y x |
|
|||
|
X |
1 1 x . |
(4.75) |
||
|
|
||||
|
L 2 |
|
|||
112

СибАДИ1 |
||||||||||||||||||
|
Рис. 4.11. Расчетная схема поперечного |
|
|
|||||||||||||||
|
криволинейного профиля (лобовой поверхности) |
|
||||||||||||||||
|
|
|
|
|
|
|
|
ра очего органа |
|
|
|
|||||||
|
учетом выражений (4.74), (4.75) интеграл (4.73) примет вид |
|||||||||||||||||
|
N pо |
L |
Y x P(x) Q( y) dx dy |
|||||||||||||||
|
2 |
|||||||||||||||||
|
|
|
L |
|
1 |
|
|
|
1 |
|
|
|
|
(4.76) |
||||
|
pо |
|
Q y d y P x dx Y x , |
|
|
|||||||||||||
|
|
|
|
|||||||||||||||
|
|
2 |
|
|
1 |
|
|
|
|
|
1 |
|
|
|
|
|||
|
|
|
|
|
|
1 |
|
2 |
|
|
|
|
|
|
|
|
||
где |
Q(y) |
ay |
|
|
; |
|
|
|
|
|
(4.77) |
|||||||
|
|
2 |
) |
2 |
|
|
|
|||||||||||
|
|
|
|
|
(1 by |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
1 |
1 x e a3 4 1 x |
2 |
|||||
|
P x |
1 2 a |
|
|
a |
|
|
|||||||||||
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
2 |
3 2 |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a3 |
2 |
|
|
(4.78) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
1 a |
|
|
|
|
|
|
|
|
|
1 x |
. |
|
|
||||
|
|
|
a 1 x e 4 |
|
|
|
||||||||||||
|
|
|
|
2 |
3 |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
113
В формуле (4.76) положим
|
|
x d0 |
P0 x d1 |
P1 x ... d P x , |
|
|||||||||||||
|
Y x di Pi |
(4.79) |
||||||||||||||||
|
i 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
где di – неизвестный постоянный коэффициент, подлежащий определе- |
||||||||||||||||||
нию; Pi x – полиномы Лежандра, вычисляемые из выражения |
|
|||||||||||||||||
|
|
|
|
|
1 |
|
|
|
|
2 |
|
i |
|
i |
|
|||
|
Pi |
x |
|
|
|
|
|
|
|
|
|
x |
|
1 |
|
|
, |
(4.80) |
|
|
|
|
|
|
|
|
i |
|
|||||||||
СибАДИ |
||||||||||||||||||
где i – про зводная i-го порядка. |
|
i |
!2 |
|
|
|
|
|
|
|
|
|
||||||
В частности меем |
|
P0 x l; |
|
|
|
|
|
(4.80, а) |
||||||||||
|
|
|
P1 x x; |
|
|
|
|
|
(4.80, ) |
|||||||||
|
|
P x |
1 |
3x2 1 ; |
|
|
|
(4.80, в) |
||||||||||
|
|
2 |
|
|
2 |
|
|
|
|
|
|
|
|
|
||||
|
|
P x |
1 |
5x2 |
3x ; |
|
|
|
(4.80, г) |
|||||||||
|
|
3 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|||
|
|
P x |
1 |
35x4 |
30x2 3. |
|
(4.80, д) |
|||||||||||
|
|
4 |
8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Графики функций (4.80, а) – (4.80, г) представлены на рис. 4.12. |
||||||||||||||||||
Площадь рабочего органа землеройной машины переменной ширины |
||||||||||||||||||
с учетом выражения (4.79) составляет |
|
|
|
|
|
|
|
|
|
|||||||||
|
L |
1 1 |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
S 2 Y X dX 2 di Pi x dx L L di Pi x dx |
|
|||||||||||||||||
|
0 |
1 i 0 |
|
|
|
|
|
|
|
|
|
2 |
|
1 i 1 |
|
|
(4.81) |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
L di Pi x dx 2L d0. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
i 0 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
В преобразованиях последнего выражения (4.81) использовано свой- |
||||||||||||||||||
ство ортогональности полиномов Лежандра, справедливое при i j : |
||||||||||||||||||
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Pi x P j x dx 0 |
|
|
|
|
|
(4.82) |
|||||||||||
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
114

СибАДИ |
|||
x |
|
|
|
Рис. 4.12. Графики функции Pi |
x 1 |
x2 |
1 i i |
Откуда следует, что: |
i!2i |
|
|
|
|
|
|
1 |
|
|
|
Pi x dx 0 при i 0; |
(4.83) |
||
1 |
|
|
|
1 |
1 |
|
|
P0 x dx 1 dx 2. |
(4.84) |
||
1 |
1 |
|
|
Таким образом, ряд (4.79) определяет различные формы лобовой поверхности рабочего органа (семейство геометрических фигур), имеющие одинаковые площади сечения.
Из выражения (4.81) следует, что площадь поверхности рабочего органа, поперечный профиль (лобовая поверхность) которого определяется разложением в ряд по ортогональным полиномам Лежандра (4.79), зависит только от первого коэффициента Лежандра d0. Это означает, что различные поперечные профили поверхности рабочего органа, определяемые разложением в ряд Лежандра (4.81), имеют при одинаковых коэффициентах первого члена, но разных коэффициентах других членов, одинаковые площади.
115
Это обстоятельство может быть использовано для определения оптимальной формы поперечного профиля, при котором результирующее нормальное усилие на наконечник минимально. То есть из всего семейства геометрических фигур ряда (4.79) необходимо выбрать такую, для которой давление на поверхность рабочего органа минимально.
Для этого необходимо определить соответствующие коэффициенты
di (i 0). |
|
|
|
|
|
|
|
|
|
|
|
СибАДИ |
|||||||||||
При i 0 |
из выражения (4.81) следует, |
|
|
|
|||||||
|
|
|
|
|
|
d0 |
S |
. |
|
|
(4.85) |
|
|
|
|
|
|
|
2L |
|
|
|
|
Если площадь сечения поверхности рабочего органа S известна, то |
|||||||||||
первый член разложен я в ряд по полиномам Лежандра d0 |
определяется |
||||||||||
формулой (4.85). |
|
|
|
|
|
|
|||||
Далее |
|
з выражен я (4.76) находим результирующее нормальное |
|||||||||
усилие на поверхность ра очего органа N с учетом разложения в ряд по |
|||||||||||
полиномам Лежандра (4.79): |
|
|
|
1 |
|
||||||
|
|
|
|
L |
1 |
|
po L |
di |
P x Pi |
x dx |
|
N p |
0 |
2 |
ky P x di Pi x dx |
2 |
ky |
1 |
|
||||
|
|
|
|
1 |
i 0 |
i 0 |
|
(4.86) |
|||
|
|
|
|
|
|
|
|
|
|
|
|
p |
o |
L |
|
|
|
|
|
|
|
|
|
|
|
|
ky Ii di, |
|
|
|
|
|
|
||
|
2 |
|
|
i 0 |
|
|
|
|
|
|
|
где k y – |
|
коэффициент, |
учитывающий неравномерность распределения |
||||||||
давления по ширине рабочего органа; |
p0 – величина нормального давле- |
||||||||||
ния в средней верхней точке поверхности рабочего органа. |
|
||||||||||
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
I i Pi x P x dx. |
|
(4.87) |
|||
|
|
|
|
|
|
1 |
|
|
|
|
|
В определенный интеграл (4.87) входят функции, определяемые вы-
ражениями (4.78) (4.80).
Влияние формы поперечного профиля наконечника на суммарную величину нормального давления N определяется согласно выражениям, находящимся под знаком суммы в выражении (4.86):
|
|
s d i I i . |
(4.88) |
i 0 |
|
Следовательно, оптимальным будет такой поперечный профиль поверхности рабочего органа, при котором ряд (4.88) имеет минимальное значение.
116
Вычислим первые члены Ii ряда (4.87): I0 = 82,81; I1 = 15,97; I2 = – 7,23; I3 = – 0,151; I4 = 0,245; I5= – 0,00123; I6 = 0,00297.
Членами I5 и большего индекса можно пренебречь, так как они не оказывают существенного влияния на результат расчета.
Ограничиваясь только пятью первыми членами ряда (4.88), задаем
целевую функцию |
|
|
|
|
|
|
|
|
|
|
СибАДИ |
||||||||||
|
|
4 |
|
|
|
|
|
|
|
|
|
|
di Ii min. |
|
(4.89) |
||||||
|
|
i 0 |
|
|
|
|
|
|
|
|
Очев дно, что значение ряда (4.79), определяющего закон изменения |
||||||||||
поперечного проф ля рабочего органа, не должно быть, по крайней мере, |
||||||||||
отрицательным в д апазоне изменения |
переменной x. То |
есть при |
||||||||
1 x 1 |
|
|
|
|
|
|
|
|
|
|
|
|
4 |
Pi x › 0. |
|
|
|||||
|
|
di |
|
(4.90) |
||||||
|
|
i 0 |
|
|
|
|
|
|
|
|
Естественно предположить, что ширина режущей кромки наконеч- |
||||||||||
ника не должна быть менее установленной величины, то есть |
|
|||||||||
|
|
4 |
|
|
|
4 |
|
|
|
|
|
|
d i |
Pi 1 di |
l, |
(4.91) |
|||||
|
|
i 0 |
|
|
i 1 |
|
|
|||
где l – полуширина режущей кромки наконечника. |
|
|||||||||
Из графиков полиномов Лежандра (см. рис. 4.12) видно, что мини- |
||||||||||
мальные значения полинома Лежандра имеются в следующих точках: |
||||||||||
P1 x при x 1; |
|
|
|
|
|
|
|
|
|
|
P2 x при x 0; |
|
|
|
|
|
|
|
|
|
|
P3 x при x 1 |
x 0,44721; |
|
|
|
|
|
|
|
|
|
P4 x при x 0,65465 |
и x 0,65465. |
|
|
|
|
|
||||
Для выполнения условия (4.90) необходимо выполнение неравенств: |
||||||||||
|
4 |
Pi 1 d0 d1 d2 d3 d4 › 0; |
|
|||||||
|
di |
(4.92) |
||||||||
|
i 0 |
|
|
1 |
|
|
3 |
|
|
|
|
4 |
Pi 0 d0 |
|
|
|
|
|
|||
|
di |
d2 |
|
d4 › 0; |
(4.93) |
|||||
|
|
|
||||||||
|
i 0 |
4 |
2 |
|
8 |
|
|
|||
|
|
Pi 0,44721 |
|
|
||||||
|
|
di |
› 0; |
(4.94) |
||||||
|
|
i 0 |
|
|
|
|
|
|
|
|
|
|
4 |
Pi 0,65465 |
|
|
|||||
|
|
di |
› 0; |
(4.95) |
||||||
|
|
i 0 |
|
|
|
|
|
|
|
|
|
|
4 |
Pi 0,65465 › 0. |
|
||||||
|
|
di |
(4.96) |
|||||||
i 0
117
Таким образом, имеем целевую функцию (4.89) при ограничениях (4.91) – (4.96). Следовательно, задача поиска оптимального поперечного профиля рабочего органа сводится к задаче линейного программирования, при решении которой находятся коэффициенты разложения di по полиномам Лежандра.
овершенно очевидно, что оптимальное решение целевой функции
(4.89) зависит от вида ограничений задачи. Поэтому рассмотрим различные виды ограничений.
СибАДИНепр емлемый с практической точки зрения, он математически вполне корректен, так как при этом получается нулевое, а следовательно, самое мин мальное значение целевой функции (4.89).
Огран чен е 1. Неотрицательность ширины рабочего органа.
Огран чен я в в де неравенства (4.90), то есть условия неотрица-
тельности аппл кат гран чной линии поперечного профиля, приводят к результату (р с. 4.13)
y x 0. |
(4.97) |
Огран чен е 2. Ограничение ширины режущей кромки неотрицательность ширины ра очего органа.
Если к неравенствам (4.90) добавить неравенство (4.91), лимитирующее минимально возможное значение полуширины режущей кромки рабочего органа, то результат решения задачи будет представлен в виде графика поперечного профиля от относительной длины рабочего органа
(рис. 4.14).
Это решение неприемлемо хотя бы потому, что указанный наконечник не будет обладать необходимой прочностью.
118

119
СибАДИ |
l |
|
||||
y x 0 |
y x 0, |
y 1 |
|
|||
Рис. 4.13. График профиля наконечника, |
Рис. 4.14. График профиля наконечника, полученный |
|||||
полученный из условия |
из условия ограничения ширины режущей кромки |
|||||
неотрицательности ширины |
неотрицательности ширины |
|
||||
рабочего органа |
рабочего органа ( y x |
|
0, |
y 1 |
|
l ) |
|
|
|
||||
3

Ограничение 3. Условие ограничения ширины наконечника. |
|
При распространении неравенства (4.91), то есть при |
|
y x l, |
(4.98) |
на весь интервал изменения x 1;1 решение задачи представляется в виде |
|
отрезка |
|
y x l, |
(4.99) |
СибАДИ |
|
график которого представлен на рис. 4.15.
y x l
Рис. 4.15. График профиля наконечника, полученный из условия ограничения ширины наконечника ( y x l)
Отметим, что полученное решение совпадает с выражением (4.98), в котором знак неравенства заменяется на знак равенства.
Если условие (4.98) полностью обосновано, то полученное решение задачи вполне приемлемо.
Ограничение 4. Условие обеспечения прочностной защиты рабочего органа при столкновении с непреодолимым препятствием.
Рассмотрим ограничение с точки зрения обеспечения прочностной защиты рабочего органа при столкновении с непреодолимым препятствием, расчетная схема для которого приведена на рис. 4.16.
120

СибАДИ |
|||||||||
Рис. 4.16. Расчетная схема для определения конфигурации поперечного |
|||||||||
проф ля по услов ю о еспечения прочностной защиты рабочего органа |
|||||||||
|
при столкновении с непреодолимым препятствием |
|
|||||||
(Т – с ла тяги рыхл теля, hн, hк – ширина боковых граней наконечника |
|||||||||
|
в верхней части и на режущей кромке, αp − угол рыхления) |
||||||||
Считая, что сечение наконечника испытывает совместное действие |
|||||||||
изгибающего момента |
|
|
|
|
|
|
|||
|
M T sin α р L x |
(4.100) |
|||||||
нормальной силы |
|
|
|
|
|
|
|||
|
|
|
P T cos αр , |
(4.101) |
|||||
запишем условие прочности произвольного сечения наконечника: |
|||||||||
|
|
|
M |
|
|
|
P |
, |
(4.102) |
|
|
|
2 nh2 |
|
2nh |
||||
|
|
|
|
|
|
|
|||
где σ |
6 |
|
|
|
|
|
|
||
– допустимое напряжение |
на |
изгиб материала |
наконечника; |
||||||
n y x |
– уравнение линии поперечного профиля; h – ширина боковых |
||||||||
граней наконечника в произвольном сечении.
Из расчетной схемы нетрудно получить уравнение ширины наконеч-
ника |
|
hк hн 1 x . |
|
h h |
н |
(4.103) |
|
|
2 |
|
|
|
|
|
121

Подставляя выражения (4.100) и (4.101) в условие (4.102), после необходимых преобразований получим искомое ограничение по прочности
|
|
3 T sin |
α |
1 x L |
T cos α |
|
|
|
|
|
|
|
|||||
2 |
|
2h |
|
|||||
y x |
|
2h |
|
|
|
. |
(4.104) |
|
|
|
|
σ |
|
||||
|
|
|
|
|
|
|
||
Полученное выражение (4.104), учитывая формулу (4.101) для вы- СибАДИчисления h, представляет собой сложную нелинейную зависимость.
График решения (4.104) для следующих исходных данных приведен на рис. 4.17: T = 250 000 H; hк = 15 мм; hн = 180 мм; L = 250 мм; αp = 30º, [σ] = 200 МПа.
Рис. 4.17. График профиля рабочего органа, полученный из расчета обеспечения прочностной защиты рабочего органа при столкновении с непреодолимым препятствием
График оптимального профиля наконечника, удовлетворяющего условию равнопрочности (4.104), представлен на рис. 4.18.
Используя известную методику, находим оптимальный режущий профиль зуба экскаватора, задаваясь ограничением по прочности по фор-
муле (4.46) (рис. 4.19).
122

СибАДИРис. 4.18. Граф ки профилей наконечников, полученные: 1 – з расчета на прочность; 2 – из условия минимизации
сопротивления рыхлению с учетом обеспечения прочности
Рис. 4.19. Графики профилей зуба ковша экскаватора, полученные: 1 – из расчета на прочность; 2 – из условия минимизации сопротивления рыхлению и с учетом обеспечения прочности
123
Оптимальный профиль практически полностью совпадает с равнопрочным, за исключением области режущей кромки наконечника. Оптимальный профиль имеет большую площадь и в состоянии воспринимать большее нормальное усилие, чем равнопрочный. Однако он воспринимает такое же удельное давление, что и равнопрочный. Введем понятие величины удельного давления. Под величиной удельного давления ki понима-
ется отношение результирующего нормального усилия Ni на профиль на- |
|||
СибАДИ |
|||
конечника к его площади Si: |
|
||
ki |
Ni |
. |
(4.105) |
|
Si |
|
|
k1 = 46,2. |
|
||
Огран чен е 5. Условие равнопрочности наконечника и ограничения ширины режущей кромки наконечника.
Если к услов ю прочности наконечника (4.104) добавить требование по ограничен ю ш р ны режущей кромки, то это приведет к увеличению давления на грунт со стороны режущей кромки, и, как следствие, улучшению процесса рыхлен я грунта. То есть с учетом выражения (4.104) и ограничения ширины режущей кромки получим профиль наконечника с учетом ограничения 5 (рис. 4.20):
T cos α |
р |
|
|
y x |
σ |
, |
(4.106) |
2 hн |
|||
Можно утверждать, что полученный оптимальный профиль с учетом ограничения 5 лучше предыдущего, так как расчетное удельное давление на него меньше k1 и составляет k2 = 43,2.
Ограничение 6. Условие равнопрочности ограничения ширины наконечника выше режущей кромки.
В частном случае, когда ограничение по ширине равно максимальной ширине равнопрочного наконечника, то получаем оптимальный профиль, представляющий собой прямую линию, касательную к кривой равнопрочного наконечника и проходящую через точку с максимальной ординатой равнопрочного наконечника (рис. 4.21). Расчетное удельное давление, приходящееся на полученный профиль наконечника, составляет k 3 41,4, что меньше, чем у предыдущих наконечников.
124

125
СибАДИ |
|
Рис. 4.20. Графики профилей наконечников равной |
Рис. 4.21. Графики профилей наконечников равной |
прочности (штриховая линия) оптимального |
прочности (кривая линия) и оптимального профиля |
профиля по условиям (4.103) и (4.106) (сплошная линия) |
с учетом ограничения 6 (прямая линия) |
3

Расчетная относительная площадь наконечника составила S3 = 138 см2. Известно, что при увеличении относительной площади наконечника удельное давление на него падает. При попытке увеличения площади наконечника до величиныS4 = 140 см2 удельное давление составило k 4 40,07.
Это меньше, чем давление оптимального профиля с учетом ограничения 6 (см. рис. 4.21). Однако из рис. 4.22 видно, что профиль, получен-
ный для S = 140 см2 и k 40,07, резко увеличивает свою ширину к верх- СибАДИней части4наконечника до4 значения полуширины, равного 11 см.
Рис. 4.22. Профиль наконечника, полученный для F4 = 140 см2 и k 4 40,07
Это ведет к неоправданному увеличению габаритов и металлоемкости не только наконечника, но стойки зуба рыхлителя, так как удельное давление на наконечник снижается лишь на 3 %.
Ограничение 7. Условие обеспечения прочностной защиты рабочего органа при реализации максимального тягового усилия.
Используя известную методику расчета на прочность и расчетную схему, приведенную на рис. 4.23, определим конфигурацию оптимального поперечного профиля из условия обеспечения прочностной защиты рабочего органа при реализации максимального тягового усилия.
126

h |
н |
|

 dL1
dL1
P
Q
z
СибАДИ |
||||||||
d |
х |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
h |
к |
|
|
|
|
|
|
|
X |
|
|
|
|
|
q |
|
|
|
|
|
|
|
|
|
|
|
Q0 |
|
|
Рис. 4.23. Расчетная схема для определения конфигурации |
|
|
||||||
поперечного профиля из условия обеспечения прочностной защиты |
|
|||||||
рабочего органа при реализации максимального тягового усилия |
|
|||||||
Интенсивность распределения нагрузки на средней линии рабочего |
||||||||
органа определяется выражением |
|
|
|
|
|
|
||
|
|
q dQ P 1 f tgα1 L, |
|
(4.107) |
||||
|
|
dx |
|
|
|
|
|
|
где α1 – угол наклона рабочей поверхности к средней линии рабочего ор- |
||||||||
гана. |
|
|
|
|
|
|
|
|
С учетом зависимости |
q dQ k |
|
|
|
|
|
||
|
|
у |
p P( x)Y x L |
|
(4.108) |
|||
|
|
dx |
|
|
0 |
|
|
|
условие равнопрочности рабочего органа при реализации максимального тягового усилия можно записать в виде
127
М |
h |
2 |
Y x |
|
|
|
|
x |
|
|
, |
(4.109) |
|
|
|
3 |
|
|||
|
|
|
|
|
|
|
где M, hx – соответственно изгибающий момент и толщина рабочего органа в произвольном сечении.
Тогда выражение (4.108) примет вид
q |
dQ |
|
3M kу p0 P( x) L |
. |
(4.110) |
||
СибАДИ |
|||||||
|
dx |
|
hx2 |
|
|||
Из расчетной схемы видно, что |
hн hк x. |
|
|||||
hx hк |
(4.111) |
||||||
|
|
d M |
LQ. |
(4.112) |
|||
dx
Выражен я (4.110) (4.112) представляют собой систему дифференциальных уравнен й относительно неизвестных M и Q.
Для решен я этой с стемы необходимы начальные условия. Очевидно, что на режущей кромке при x = 0 величина изгибающего момента рав-
на нулю, т.е. |
|
|
|
M M0 |
0, |
|
|
|
|
|
(4.113) |
|
|
|
|
|
|
|
|
|
a3 ) h |
||||
Q Q |
p |
0 |
P(0)h |
b f p |
0 |
(1 2a |
2 |
a |
3 |
e |
b f . (4.114) |
|
0 |
|
k |
k |
|
|
|
k |
k |
||||
После решения системы уравнений (4.110) |
и (4.112) |
с учетом на- |
||||||||||
чальных условий (4.113) и (4.114) из формулы (4.109) можно определить полуширину Y(x) ра очего органа при условии обеспечения прочностной защиты рабочего органа для реализации максимального тягового усилия:
Y x |
3 М |
|
σ h 2x . |
(4.115) |
График оптимального профиля наконечника, удовлетворяющего условию равнопрочности (4.115), представлен на рис. 4.24.
Вывод. С точки зрения обеспечения защиты зуба ковша экскаватора наконечника зуба рыхлителя от разрушения при разработке мерзлых грунтов и при внезапном столкновении с непреодолимым препятствием оптимальными будут являться поперечные профили, рассчитанные с учетом ограничений и приведенные на рис. 4.18−4.21 и 4.24. Рабочие органы с профилями, представленными на рис. 4.18−4.21, рекомендуются для мерзлых грунтов с каменистыми включениями. Указанные профили обеспечат минимизацию силы сопротивления разработке грунта, снижение
энергоемкости процесса.
128

СибАДИРис. 4.24. График профиля наконечника, полученный из расчета о еспечения прочностной защиты рабочего органа
при реализации максимального тягового усилия
Недостатком профилей ло овой поверхности (см. рис. 4.18 – 4.20) является усложнение технологии их изготовления. Рабочий орган с профилем, показанным на рис. 4.24, рекомендуется для разработки плотных абразивных грунтов. Прямолинейный профиль рабочего органа (см. рис. 4.21) удовлетворяет условию прочности и обладает меньшим удельным давлением. Кроме этого, он технологически прост в изготовлении.
Следует отметить, что вопрос об оптимальном поперечном профиле наконечника не исчерпан, так как могут существовать другие ограничения для расчета оптимального профиля.
4.3. Определение анализ конфигурации оптимального поперечного сечения лобовой поверхности рабочего органа
Известны наконечники зубьев рыхлителей как плоской, так и различной криволинейной геометрии рабочей поверхности. Актуальным является вопрос оптимальности конфигурации поверхности рабочего органа с точки зрения минимизации сопротивления рыхлению, а значит, и увеличения производительности, и снижения энергоемкости процесса рыхления.
129

Поставим задачу определения оптимального поперечного сечения лобовой поверхности рабочего органа землеройной машины. Рассмотрим решение данного вопроса на примере наконечника зуба рыхлителя.
вяжем с наклонно установленным наконечником декартовую систему координат x y z таким образом, чтобы ось x проходила по средней образующей цилиндрической поверхности наконечника, а ось y распола-
галась в горизонтальной плоскости (рис. 4.25). |
|
|
|
|
|
||
СибАДИ |
|||||||
Рис. 4.25. Схема сил, действующих на элементарную |
|
||||||
поверхность криволинейного рабочего органа |
|
||||||
Пусть уравнение поверхности рабочего органа (наконечника) в сис- |
|||||||
теме координат x y z имеет вид |
|
|
|
|
|
||
|
|
z f y . |
|
|
|
|
(4.116) |
|
|
|
y |
|
|
, полученную пово- |
|
Одновременно введем систему координат x |
|
z |
|||||
ротом системы x y z на угол резания αp . При этом оси x и |
z будут |
||||||
располагаться по горизонтали |
вертикали (см. рис. 4.25). Можно записать |
||||||
выражения для нахождения координат точек криволинейной поверхности |
|||||||
наконечника: |
|
|
|
|
|
|
|
x x cos α |
y 0 |
z sin α x cos α |
z sin α ; |
(4.117) |
|||
|
y x 0 y 1 z 0 |
|
y ; |
(4.118) |
|||
z x sin α |
y 0 z cos α x sin |
α z cos α . (4.119) |
|||||
Подставляя выражения (4.118) и (4.119) в уравнение (4.116), получим |
|||||||
|
z cos α x sin α f |
|
y . |
(4.120) |
|||
Преобразовав формулу (4.120), запишем |
|
|
|
|
|
||
x sin |
α f y z cos α 0. |
(4.121) |
|||||
130

Выделим на поверхности наконечника бесконечно малую произвольную площадку dS, на которую действует нормальное усилие dN и сила трения dT (см. рис. 4.25).
Очевидно, что элементарное нормальное усилие будет определяться зависимостью
dN P dS , |
(4.122) |
где Р – величина нормального давления на наконечник, определяемая по |
|||||||||||||||||||||||||||||
СибАДИ |
|||||||||||||||||||||||||||||
формуле |
|
|
|
P p0 |
Q y P x , |
|
|
|
|
|
(4.123) |
||||||||||||||||||
здесь p0 − вел ч на нормального давления в средней верхней точке рабо- |
|||||||||||||||||||||||||||||
чего органа; |
Q y , P x |
– функции, учитывающие изменение давления |
|||||||||||||||||||||||||||
по ширине |
дл не ра очего органа (наконечника) соответственно. |
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
X |
|
a3 |
|
|
X 2 |
|
|
|
|
|||||||||
|
|
P x 1 2 a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
2 |
|
3 |
|
|
|
|
L |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Y 2 |
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
1 a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
Q y |
|
|
|
|
|
l |
|
|
|
|
, |
|
|
|
|
(4.125) |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
Y 2 |
|
2 |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
1 b |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
l |
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
где L, l – соответственно длина |
|
полуширина наконечника; X, Y – абсолют- |
|||||||||||||||||||||||||||
ные координаты произвольной точки поверхности наконечника; x, y – отно- |
|||||||||||||||||||||||||||||
сительные координаты точек поверхности наконечника. |
|
||||||||||||||||||||||||||||
Элементарная величина силы трения, действующего на произволь- |
|||||||||||||||||||||||||||||
ную площадку dS, будет равна |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
dT f dN f PdS . |
|
|
|
(4.126) |
|||||||||||||||||||||
Горизонтальная сила, действующая на элементарную площадку dS, |
|||||||||||||||||||||||||||||
будет определяться по следующей зависимости: |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
d Eг dN cosβ dT cosα . |
|
|
(4.127) |
||||||||||||||||||||||||
Площадь произвольной элементарной площадки |
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
||
|
dS dl dx |
|
d z2 d y2 dx 1 |
|
|
|
dxdy |
|
|||||||||||||||||||||
|
|
d z |
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(4.128) |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
d y |
|
|
|
|||||
|
|
|
dxdy |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
1 f y 2 |
1 z 2dxdy, |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
где β – угол наклона нормального усилия dN к оси |
x , находящийся по |
||||||||||||||||||||||||||||
формуле |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
131

cos β |
|
|
|
|
|
x |
|
. |
(4.129) |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
2 |
2 |
|
|
|
|||||
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
x |
|
|
y |
|
z |
|
|||||
Найдем частные производные, входящие в последнюю формулу, ис-
СибАДИ |
||||||||||||||||||||||||
ходя из функции (4.121): |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
sin |
α ; |
|
|
|
|
|
(4.130) |
|||||
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
f y z ; |
|
|
|
(4.131) |
|||||||||||||
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
cos α . |
|
|
|
|
|
(4.132) |
|||||||||||
|
|
|
|
|
|
z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Подставляя полученные выражения (4.130) – (4.132) в формулу |
||||||||||||||||||||||||
(4.127), наход м |
|
|
|
|
|
|
|
|
|
|
sinα |
|
|
|
sinα |
|
||||||||
|
|
|
|
cosβ |
|
|
|
|
|
|
|
|
|
|
1 z 2 . |
(4.133) |
||||||||
|
|
|
|
|
|
|
|
|
|
1 f y 2 |
||||||||||||||
учетом зависимостей (4.122), (4.126), (4.128) и (4.133) выражение |
||||||||||||||||||||||||
(4.127) принимает вид |
|
|
sinα |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
dEг P 1 z 2 dxdy |
|
f P |
1 z 2 dxdycosα |
|||||||||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||||
1 z 2 |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(4.134) |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
P sinα dxdy f Pcosα |
1 z 2 |
dxdy. |
|
|
|
|
|
|
||||||||||||||||
Интегрируя полученное выражение (4.134) по всей поверхности на- |
||||||||||||||||||||||||
конечника, получим |
|
[P sin |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dx dy ] |
|||
E г |
|
|
|
|
|
|
|
|||||||||||||||||
α dx dy |
|
f P cos |
α |
1 z 2 |
||||||||||||||||||||
|
|
S |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p0 |
P x Q y sin |
α |
dx dy |
|
|
|
|
|
(4.135) |
||||||||||||||
|
|
P x Q y f |
|
|
|
|
|
|
|
|
|
|||||||||||||
p0 |
cos |
|
α |
|
1 |
z 2 |
|
dx dy |
|
|||||||||||||||
Первое слагаемое в полученном выражении не зависит от формы криволинейного профиля наконечника z f y . Поэтому в дальнейших рассуждениях будем рассматривать только второе слагаемое, которое является проекцией суммарной силытрениянаповерхностьрабочего органа.
Запишем
Eтр p0 |
P x Q y f cos α |
1 z 2 dx dy . |
(4.136) |
132

Упрощая выражение (4.136), получим
|
|
|
|
|
|
L |
|
|
|
|
|
|
|
|
|
|
l |
|
|
|
|
|
|||||||
Eтр p0 f |
cos α P |
x dx Q y |
1 z 2 |
dy . |
(4.137) |
||||||||||||||||||||||||
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
l |
|
|
|
|
|
|||||
В полученном выражении (4.137) от формы криволинейной поверх- |
|||||||||||||||||||||||||||||
ности зависит лишь последний интеграл |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
l |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Q y |
1 z |
2 |
|
|
dy. |
(4.138) |
|||||||||||||||||||
СибАДИ |
|||||||||||||||||||||||||||||
|
|
|
l |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Пр мен м к нтегралу (4.138) известную формулу Эйлера |
|
||||||||||||||||||||||||||||
|
F y,z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
d Fz |
y,z |
|
|
|
|
|
||||||||||||||||||||
|
z |
|
|
|
|
|
|
d y |
|
|
0, |
(4.139) |
|||||||||||||||||
где |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
F y,z Q y |
|
1 z 2 |
. |
|
|
|
|
(4.140) |
||||||||||||||||||||
Тогда |
|
|
F y,z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
z |
|
|
|
|
|
0. |
|
|
|
|
(4.141) |
|||||||||||
Из уравнен я (4.139) и выражения (4.140) следует, что |
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z |
|
|
|
|
С const , |
(4.142) |
||||||||
|
Fz |
y,z Q y |
|
|
|
|
|
|
|
|
2 |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 z |
|
|
|
|
|
|
|
|
|
|||||
где С – неопределенная константа. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Из полученного выражения можно записать: |
|
||||||||||||||||||||||||||||
|
|
Q y z С |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
1 z 2 |
. |
(4.143) |
||||||||||||||||||||
Тогда с учетом преобразований (4.144) – (4.147): |
|
||||||||||||||||||||||||||||
|
|
Q2 y z |
2 |
|
|
|
1 z 2 , |
(4.144) |
|||||||||||||||||||||
|
|
Q2 y z |
2 |
|
|
С z 2 |
|
С, |
(4.145) |
||||||||||||||||||||
|
|
z |
2 |
|
|
|
|
C |
|
|
|
|
|
|
, |
|
|
|
|
|
|
|
|
(4.146) |
|||||
|
|
Q2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
y C |
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
z |
|
|
|
|
|
|
|
C |
|
|
|
|
|
|
, |
|
|
|
|
|
|
|
|
(4.147) |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
Q2 |
y C |
|
|
|
|
|
|
|
|
|
||||||||||||
следует |
|
|
l |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
C |
|
|
dy. |
(4.148) |
|||||||||||||||
|
|
z |
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
l |
|
|
|
Q |
2 y C |
|
|
|
|
|
|||||||||||||||
133
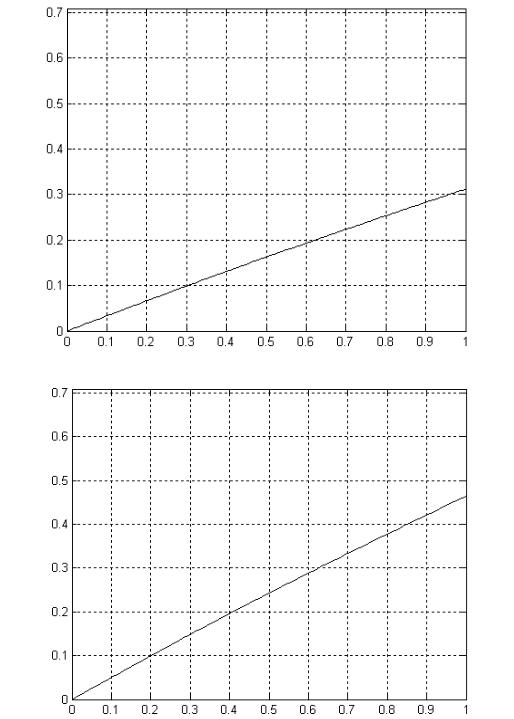
Анализируя подынтегральное выражение (4.148), нетрудно заметить, что 0 C 1. Задаваясь значениями С, определены различные варианты оптимальных профилей рабочих поверхностей наконечника зуба рыхли-
теля (рис. 4.26 – 4.29).
z
СибАДИz Рис. 4.26. Оптимальная ра очая поверхность при = 0,1 C
Рис. 4.27. Оптимальная рабочая поверхность при С = 0,2
C
134
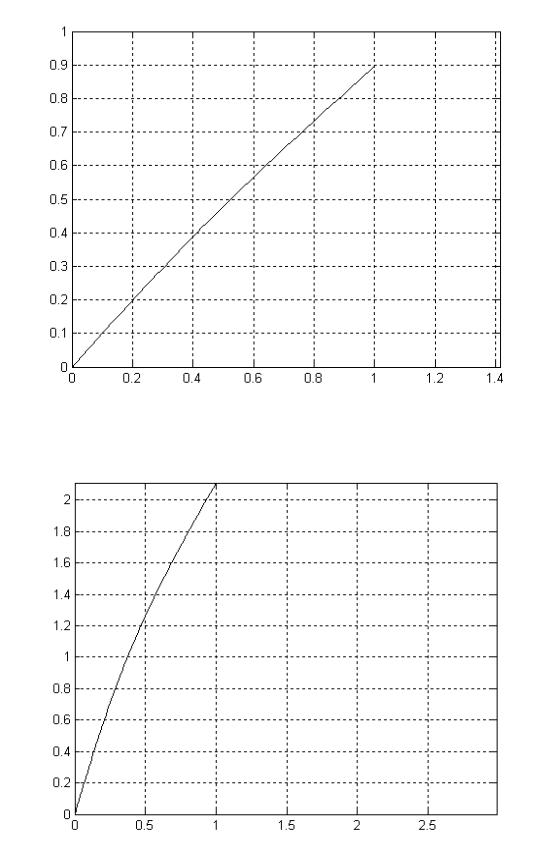
z
СибАДИz Рис. 4.28. Оптимальная ра очая поверхность при = 0,5 C
C
Рис. 4.29. Оптимальная рабочая поверхность при С = 0,9
135

По полученным данным построим график зависимости функционала
(4.138) от константы С (рис. 4.30).
СибАРис. 4.30. Зав симость функционалаДllQ y 1 Иz 2 dy от неопределенной константы С
В силу симметричности ра очего органа рыхлителя на рисунках приведены половины поперечных сечений профиля.
Из выражения (4.146) можно видеть, что значение функционала (4.137) зависит от константы С. Поэтому, задаваясь различными значениями константы С в диапазоне (0; 1) и подставляя полученные значения выражений (4.125) и (4.147) в функционал (4.138), определяем его численное значение.
Из графика, представленного на рис. 4.30, следует, что наименьшее значение функционала, а следовательно, сопротивления разработке, определяемого из выражения (4.135), соответствует постоянной С = 0. Таким образом, исходя из формулы (4.148), геометрия оптимальной лобовой поверхности рабочего органа соответствует прямолинейной конфигурации, когда z = 0.
Основываясь на вышеизложенном, можно утверждать, что величина пространственного распределения напряжений, приходящихся на контактную поверхность рабочего органа, определяет различные его конфигурации. Характер распределения напряжений зависит от факторов разработки: типа грунта, его физико-механических свойств, температуры, влажности, максимального тягового усилия трактора, скорости и глубины
136

разработки мерзлого грунта. Представленная методика позволяет получать различные конфигурации оптимальных форм контактных поверхностей рабочих органов в зависимости от вариации факторов разработки с точки зрения минимизации энергоемкости процесса разработки мерзлых грунтов.
СибАДИРис. 4.31. Конф гурац я опт мальной формы рабочего органа рыхлителя для разработки мерзлого песчаного грунта с каменистыми включениями
влажностью 10−15% при температуре (– 5…– 8) ºС, глуб не разработки 0,7−0,8 м, максимальном тяговом усилии 300 кН,
на первой передаче скорости 0,69−0,75 м/с
Рис. 4.32. Конфигурация оптимальной формы рабочего органа рыхлителя для разработки мерзлого глинистого грунта влажностью 30 %
при температуре (– 3…– 5) ºС, глубине разработки 1,0−1,2 м, максимальном тяговом усилии 250 кН, на первой передаче и скорости 0,75−0,83 м/с
На рис. 4.31, 4.32 приведены примеры рабочих органов землеройных машин, полученных по представленной в главе методике оптимизации с учетом различных факторов разработки мерзлых грунтов.
137
