
1894
.pdf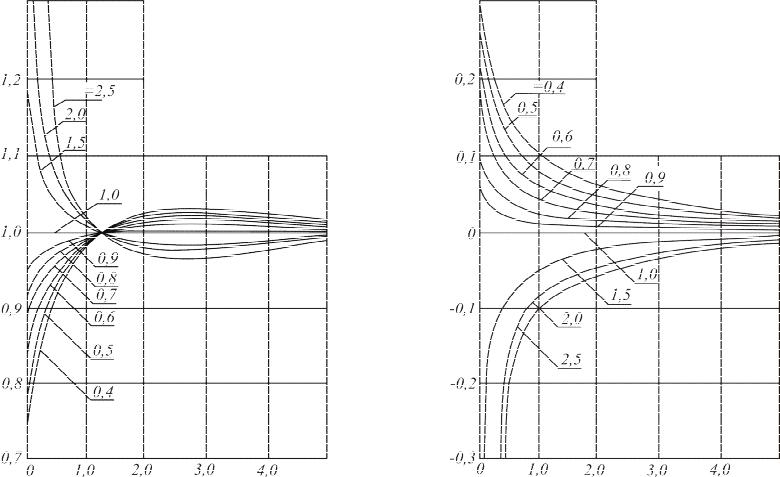
AП |
AО |
Ω |
Ω |
|
37
Pdh |
Pdh |
Рис. 2.9. Относительные амплитуды падающей АП и отраженной АО температурных волн на поверхности двухслойной полуограниченной среды в зависимости от числа Предводителева Рdh(1) и отношения коэффициентов тепловой активности слоев kв
φП
Ah
Ω
Ω
Ω
Pdh
38
Pdh
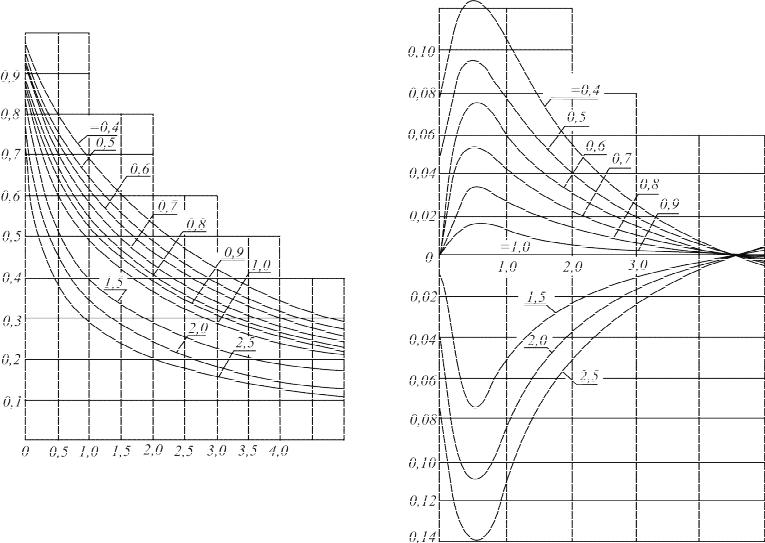
Рис. 2.10. Относительная амплитуда температурной волны на контакте слоев двухслойного полуограниченного тела Ah , смещение по фазе φП в зависимости от числа Предводителева Рdh(1) и отношения коэф-
фициентов тепловой активности слоев kв
3
Положив в (2.55) или (2.56) Кв = 1, получим решение Фурье для однородного полуограниченного тела (2.34).
Физическая сторона влияния термической разнородности на температурный режим слоистого полуограниченного тела сводится к следующему. Амплитуда плотности теплового потока в термическом однородном полуограниченном теле пропорциональна его коэффициенту тепловой активности (2.43). В двухслойной среде с в1 = = в её полуограниченная часть с коэффициентом тепловой активности в2 не обеспечивает такой же транзит плотности теплового потока, что и в однородном теле с коэффициентом в = в1 . Если в1 > в2 , то плотность теплового потока в ней меньше, а если в1 < в2 , то больше нежели в верхнем слое. В итоге, в первом случае имеет место подпор тепла на границе раздела сред, описываемый отраженной волной положительного знака.
Во втором случае, когда в1 < в2 , нижний слой отводит тепло интенсивнее от верхнего слоя, вследствие чего отраженная температурная волна в первом слое меняет знак на отрицательный.
Отраженная температурная волна складываясь с падающей, обуславливает в первом случае повышенную, а во втором пониженную, относительно однородной среды с теплофизическими свойствами а1 = а и в = в1 , амплитуду суммарной волны.
2.7. Температурное поле однородного полуограниченного тела при случайном изменении температуры среды
Допустим температура среды t(τ) изменяется как стационарный нормальный процесс с постоянным математическим ожиданием mt и корреляционной функцией Kt(τ) . Требуется определить статистические параметры температурного поля полуограниченного тела в квазиустановившемся режиме.
Из теории случайных функций известно [3], что линейная система преобразует входной стационарный нормальный случайный процесс в такой же процесс, но с иными математическими ожиданием и дисперсией. Характер преобразования системой случайной функции определяется частотной характеристикой этой системы.
Вид частотной характеристики для однородного полуограниченного тела при граничных условиях III рода следует из уравнения
(2.46):
4

|
|
|
|
|
|
|
|
|
|
ω |
|
|
|
|
|
|
||||
|
|
|
|
|
|
z |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
exp |
|
|
|
|
|
|
|
|
|
|
|
||||||
ψ z,ω = |
|
|
|
|
|
|
|
|
2a |
|
|
. |
(2.63) |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
λ |
|
|
|
|
|
ω |
λ 2 |
|
||||||||
|
1+ |
|
|
2ω |
+ |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
a |
|
a |
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||
Искомая дисперсия температуры в плоскости z тела вычисляется по формуле
|
|
Dt z = ψ2 z,ω St ω dω, |
(2.64) |
0 |
|
где St(ω) – спектральная плотность случайного процесса, связанная с корреляционной функцией Kt (τ) косинус - преобразованием Фурье:
St ω = |
2 |
Kt τ cosωτdτ. |
|
π 0 |
(2.65) |
Математическое ожидание температуры полуограниченного тела есть функция
mt z mt z , |
(2.66) |
где z – относительная амплитуда изменения температуры (2.46). В случае нормального случайного процесса с корреляционной
функцией
Kt τ = Dexp β2τ2 |
(2.67) |
его спектральная плотность, согласно (2.65), выразится уравнением
|
ω = |
D |
|
|
|
ω |
2 |
|
|
||
St |
|
|
|
|
|
|
(2.68) |
||||
|
|
|
|
|
2 |
||||||
β π |
|
exp |
4β |
. |
|||||||
|
|
|
|
|
|
|
|
||||
Пользуясь выражением (2.64), находим искомую дисперсию температуры в однородном полуограниченном теле, т.е.
|
|
|
|
|
|
|
|
|
|
|
|
|
ω |
|
|
|
|
|
|
|
|
|
ω |
2 |
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dω |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
exp 2z |
|
|
|
|
cos |
|
|
|
|
|
|
2 |
|
|
|
|
|
||||||||||||||||
|
D |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4β |
|
|
|
|
|
|
|||||||||||||
D z = |
|
|
|
|
|
|
|
|
|
|
2a |
|
|
|
|
|
|
|
, |
|
(2.69) |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
β π 0 |
|
|
λ |
|
|
|
|
|
|
|
ω |
|
|
|
λ 2 |
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
1+ |
|
2aω+ |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
α |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
α |
|
|
|
|
|
|
2 |
|
||||||||||||
что после введения новой |
переменной интегрирования |
4 |
= |
|||||||||||||||||||||||||||||||||||
4 2 |
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
безразмерных параметров θz |
= z |
β |
|
и δ = |
2λ |
|
|
|
|
β |
|
дает |
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
a |
|
|
|
|
|
α |
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
5
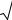
8 |
|
υexp υ4 2θ |
υ |
|
|||||
D z = D |
|
|
|
|
|
z |
|
dυ. |
(2.70) |
|
|
|
2 |
|
|
||||
π |
|
||||||||
|
|
0 |
11+δυ |
|
|
|
|
||
Интеграл в полученном выражении (2.70) следует вычислять численным способом.
2.8. Промерзание (протаивание) влажного полуограниченного тела (задача Стефана)
Изменение агрегатного состояния тела в общем случае имеет два следствия, влияющие на тепловой режим тела: при перемещении границы затвердевания выделяется скрытая теплота фазового перехода и изменяются теплофизические характеристики материала. Постановка таких задач существенно отличается от обычных задач неустановившегося режима, а именно: появляется необходимость решать систему двух уравнений теплопроводности (для мерзлой и талой областей) и помимо граничных условий на поверхностях тела дополнительно задавать два условия на границе промерзания:
1) теплового баланса
|
|
tм |
|
|
|
|
|
|
tт |
|
|
|
|
L |
dxм |
; |
(2.71) |
||
|
|
|
|
|
|
|
|||||||||||||
|
м x |
|
|
|
x xм 0 |
|
x |
|
x xм 0 |
V |
d |
|
|||||||
|
|
|
|
|
|||||||||||||||
2) равенства температур |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
t1 |
|
x xм 0 |
t2 |
|
x xм 0 |
tл. |
|
|
(2.72) |
||||||||
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|||||||||||||
Первый член левой части уравнения (2.71) выражает плотность теплового потока qм , который отводится от границы фаз через мерзлую область; второй член – плотность теплового потока qт, поступающего к границе фаз из талого грунта.
Правая часть уравнения (2.71) представляет собой плотность теплового потока, возникающего благодаря выделению скрытой теплоты фазового перехода. При промерзании значение объемной
теплоты фазового перехода |
|
LV m м, |
(2.73) |
где m – пористость тела; – теплота фазового перехода единицы массы жидкости; м – плотность затвердевшего вещества. Например, для водонасыщенного грунта при m = 0,3, = 93 Вт·ч/кг и м = 920
кг/м3 имеем: LV 0,3 93 920 25,7 103 Вт·ч/м3.
6

Рассмотрим для примера задачу промерзания полуограниченного тела при следующих краевых условиях (начало координат – на поверхности тела):
t |
0 t0 tк; |
t |
x 0 tп tк; |
|
||||||
|
|
t |
|
|
|
|
|
|
(2.74) |
|
|
|
|
|
0; |
tx t0 , |
|
||||
|
|
|
|
|
|
|
|
|||
|
|
x |
|
|
|
|||||
|
|
|
x |
|
|
|
|
|
||
|
|
|
|
|
|
|
||||
дополненных условиями (2.71) и (2.72). Решение данной задачи, которую
Стефана, имеет следующий вид: при 0 ≤ η ≤ 1 (мерзлая область)
1 t1 tп tк tп
erf |
|
1 |
|
|
|
|
||
|
|
|
|
|
|
|
||
|
Fo1 |
|
|
|||||
2 |
|
|
|
|||||
erf |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
||
2 |
Fo1 |
|
|
|||||
часто называют задачей
|
erf |
; |
(2.75) |
erf |
при 1 ≤ η ≤ ∞ (талая область)
|
|
|
|
|
|
|
|
|
|
erf |
|
|
|
1 |
|
|
|
|
|
|
|
erf Ка |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
t2 t0 |
|
|
|
|
2 |
|
|
Fo2 |
|
|
. |
(2.76) |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|||||||||||
|
2 |
|
tк t0 |
|
|
|
erf |
|
|
|
|
|
|
|
|
|
|
erf Ка |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
Здесь |
|
|
|
|
2 Fo2 |
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
a1 |
|
|
|
|
|
|
a2 |
|
|
|
|
|
|
|
|
x |
|
|
|
a1 |
|
|
|||||||
Fo |
|
; |
Fo |
|
|
|
|
; |
|
; K |
a |
|
. |
(2.77) |
||||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
1 |
|
|
x2 |
|
|
2 |
|
|
x2 |
|
|
|
|
|
|
|
x |
|
a |
2 |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
к |
|
|
|
|
|
||||
Как видим, распределение температуры в мерзлой и талой областях является функцией интеграла вероятностей Гаусса. Подставив (2.75) и (2.71) в уравнение теплового баланса на границе промерзания, получим
|
exp 2 |
ПS |
|
exp 2Ka |
|
|
|
|
||||||||||||||||
|
|
|
Ko, |
(2.78) |
||||||||||||||||||||
|
|
|
|
|
erfc |
|
|
|
|
|
||||||||||||||
|
erf |
|
|
|
|
|
||||||||||||||||||
|
|
|
|
Ka |
||||||||||||||||||||
где |
|
|
|
|
|
|
|
|
LV |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
Ko |
|
|
|
|
|
|
|
; |
|
|
|
|
(2.79) |
|||||||||
|
|
c t |
к |
t |
п |
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
1 1 |
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
t0 |
tк |
|
|
|
|
|
|
|
|
|
|
||||||||
|
П |
S |
|
|
|
|
2с2 |
2 |
; |
|
|
(2.80) |
||||||||||||
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
t |
к |
t |
п |
|
|
с |
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
1 |
|
1 |
1 |
|
|
|
|
|
|||||
7

|
|
xк |
|
. |
(2.81) |
|
|
|
|
|
|||
|
||||||
2 |
|
a1 |
|
|||
Решая это уравнение (например, графически), находим значение, что позволяет определить местоположение границы промерзания:
xм 2 |
a1 . |
(2.82) |
Решение (2.82) показывает, что продвижение |
границы |
|
промерзания не имеет предела и идет со скоростью, пропорциональной корню квадратному от времени.
Критерий Ko(Коссовича) выражает отношение количества тепла, выделяющегося при затвердевании единицы объема вещества, к количеству тепла, которое надо отвести от этого объема для его охлаждения от температуры льдообразования tл до температуры поверхности тела tп .
Критерий ПS является мерой отношения тепловых потоков (количеств тепла), подводимых к границе промерзания из мерзлой области и из талой, в предположении, что рассматривается не полуограниченное тело, а неограниченное тело с различными начальными температурами в мерзлой и талой областях, которое не зависит от времени, следовательно, и не зависит от времени.
Если в начальный момент времени температура тела равна
температуре |
затвердевания (t0 tк), |
то ПS 0 |
и уравнение (2.78) |
||||
упрощается: |
|
exp 2 |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
Ko. |
(2.83) |
||||
|
|
|
|
||||
|
|
|
|||||
|
|
erf |
|
|
|
|
|
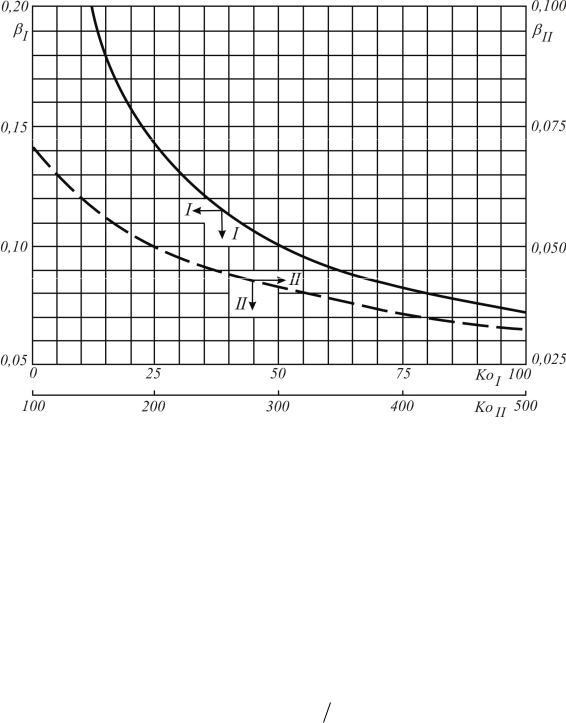
Значения f Ko , вычисленные по формуле (2.83), даны на рис. 2.11.
Решение задач с фазовыми превращениями можно значительно упростить, если заранее задаться распределением температур в мерзлой и талой частях тела. Тем самым отпадает необходимость в вычислении температур и остается только определить местоположение границы промерзания. Такой прием не требует решения уравнения теплопроводности, так как для расчета перемещения границы промерзания достаточно уравнения теплового баланса (2.71).
Рассмотрим порядок решения задач расчета границы промерзания на примере простейшей задачи: на поверхности тела температура постоянна и ниже температуры льдообразования (tп = const; tп < tк );
8
на границе промерзания тепловой поток из талого грунта qт = 0. Далее покажем, как применять это решение для более сложных случаев: когда на поверхности тела имеется один или несколько слоев теплоизоляции, в начальный момент времени часть тела находится в затвердевшем состоянии, задана не температура поверхности, а температура среды υ < tк .
Рис. 2.11. Зависимость от критерия Коссовича Ko
Пусть начальная температура полуограниченного тела равна температуре льдообразования (t0 tл ) и, следовательно, qт = 0. При постоянной температуре на поверхности тела уравнение теплового баланса (2.71) принимает вид
|
tк |
tп |
|
L |
|
dxк |
. |
(2.84) |
|||||
|
|
|
|
|
|
||||||||
1 |
|
|
xк |
|
|
|
|
V |
d |
|
|||
Если при = 0 имеем |
xм 0, |
|
то решение |
уравнения (2.84) |
|||||||||
следующее: |
|
|
|
|
|
|
xм2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
(2.85) |
||
|
2 |
t |
л |
t |
п |
|
L |
||||||
|
|
|
1 |
|
|
|
V |
|
|||||
9

Если на поверхности тела имеется слой теплоизоляции hиз , то
q |
|
|
tл tп |
, |
(2.86) |
||
|
|
|
|
||||
где |
м |
1 tл R |
|
||||
|
|
|
1 |
|
|
|
|
|
R h |
|
, |
(2.87) |
|||
|
|
|
|||||
|
|
из |
|
||||
|
|
|
|
из |
|
||
и тогда решением является
|
|
|
|
x2 |
|
|
|
|
|
|
R |
|
|
|
|
|
|
|
м |
|
|
|
|
|
|
|
|
|
xм . |
2 |
t |
л |
t |
п |
L |
|
t |
л |
t |
п |
L |
|||
1 |
|
|
V |
1 |
|
|
V |
|
||||||
Вместо (2.85) и (2.88) можно также написать:
|
|
|
|
|
|
|
|
|
|||||
xм |
2 1 tл tп |
, |
|
|
|
|
|||||||
|
|
|
|
|
|
||||||||
|
|
|
LV |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
2 t |
л |
t |
п |
|
|
||||
xм R R |
|
|
|
1 |
|
|
|
. |
|||||
|
|
LV |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|||
(2.88)
(2.89)
(2.90)
Обратим внимание, что формулу (2.88) можно представить в виде суммы двух величин:
h |
0 |
h , |
(2.91) |
t |
|
t |
|
где ht 0– время промерзания при отсутствии теплоизоляции; |
ht – |
||
дополнительное время промерзания, связанное с наличием теплоизоляции.
Таким образом, становится понятным влияние теплоизоляции: вопервых, ее эффект пропорционален ее толщине и, во-вторых, наличие теплоизоляции увеличивает время промерзания на постоянную величину на каждую единицу глубины промерзания независимо от толщины ранее промерзшего слоя.
Применение метода конечных элементов (МКЭ) позволяет решать задачи промерзания без упрощений расчетных схем.
Математическая модель общей задачи нестационарной теплопроводности с нелинейностью имеет вид
|
t |
t |
c t t |
t |
q |
0, |
(2.92) |
|
|
|
|
|
|||||
|
|
|
|
|
V |
|
|
|
xi |
|
|
|
|
|
|||
где для трехмерной задачи в прямоугольной системе координат j = =1,2,3, а теплофизические коэффициенты грунта ,c, , qV являются функцией температуры t; – время.
10

Эффективная теплоемкость влажной смеси ниже температуры ее льдообразования, tл численно равна количеству тепла, необходимого для изменений температуры единицы массы на 1°C и фазового состава в ней поровой влаги:
cэ t cм t LdWH dt, |
(2.93) |
где L – удельная теплоемкость таяния льда; dWH 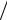 dt – изменение относительного количества незамерзшей воды от температуры.
dt – изменение относительного количества незамерзшей воды от температуры.
Численное моделирование температурного режима промерзающего грунта может быть выполнено методом конечных элементов с использованием комплекса программ для расчета нестационарного нелинейного температурного поля в трехмерной постановке. Для этого грунтовую среду следует разбить на восьмиузловые изопараметрические конечные элементы, а в качестве базисных ввести трилинейные функции формы , каждая из которых равна единице в своем узле и нулю во всех остальных. После применения процедуры Бубнова–Галеркина получаем систему обыкновенных дифференциальных равнений
|
|
C |
t |
H |
|
|
|
, |
(2.94) |
|
t |
F |
|||||||||
|
||||||||||
|
|
|
|
|
|
|
|
|
||
где C – матрица теплоемкостей; H – матрица теплопроводностей; |
||||||||||
|
|
– вектор нагрузок. |
|
|
|
|
|
|
||
|
F |
|
|
|
|
|
|
|||
|
|
Для решения системы |
обыкновенных |
дифференциальных |
||||||
уравнений можно воспользоваться конечно-разностной схемой
ti 1 ti i 1 i
C H t 1 t F , (2.95)
t
вкоторой 0 1. Если принять 1, то это приведет к неявной конечно-разностной схеме
|
1 |
|
|
i 1 |
|
1 |
|
|
i |
|
|
|
|
|
|
|
|
||||||||
|
|
C H t |
F |
|
|
C t |
, |
(2.96) |
||||
|
|
|
||||||||||
|
t |
|
|
|
|
t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
которая устойчива при любых соотношениях между шагами по временной и пространственным координатам.
Полученная система линейных уравнений решается методом сопряженных градиентов с учетом симметричности и разрешенности матрицы жесткости.
11
