
1894
.pdf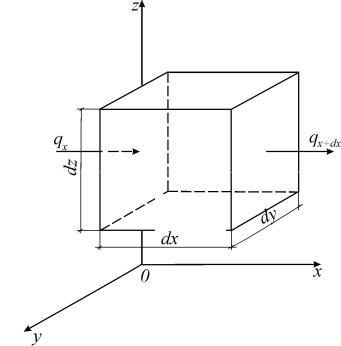
Скалярная величина вектора плотности теплового потока определяется по формуле
q gradt, |
(1.3) |
где – коэффициент теплопроводности, т.е. плотность теплового потока пропорциональна градиенту температур.
Уравнение (1.3) является математической формулировкой закона Фурье.
Полное количество тепла, проходящее за время τ через изотермическую поверхность F, равно
|
|
Q τ = q dFd . |
(1.4) |
0F
1.3.Дифференциальное уравнение теплопроводности
Воснову вывода дифференциального уравнения теплопроводности положен закон сохранения энергии, который в рассматриваемом случае может быть сформулирован следующим образом: количество тепла, выведенное в элементарный объем извне за время dτ вследствие теплопроводности dQ1 , а также внутренних источников dQ2 , равно изменению внутренней энергии вещества dQ , содержащегося в элементарном объеме
dQ1 + dQ2 = dQ. |
(1.5) |
c
Рис.1.2. К выводу уравнения теплопроводности
12
Выделим элементарный объем в однородном и изотропном теле (рис.1.2). Через грань элементарного объема dxdydz проходит теплота в количестве qxdydz. При
нестацио-нарном тепловом пото-ке элементарный объем будет нагреваться (охлаждаться). По закону сохранения количества теплоты проходящее
через грань dydz будет меньше (больше) на ве-личину теплоты, аккумулированной в элементарном объеме. Составим уравнение теплового баланса по оси Ox:
qxdydz qx+dxdydz= c |
t |
dxdydz, |
(1.6) |
|
|||
|
τ |
|
|
где с – удельная теплоемкость материала; – плотность материала. Раскладывая функцию qx+dx в ряд Тейлора и ограничиваясь двумя
членами ряда (первой степенью бесконечно малой величины), получим
qx+dx |
= qx |
+ |
qx |
dx. |
(1.7) |
|
|||||
|
|
|
x |
|
|
Подставляя этот ряд в уравнение (1.6), имеем
qx |
= c |
t |
. |
(1.8) |
|
|
|||
x |
τ |
|
||
Опустив знак минус в уравнении (1.3) и продифференцировав его по x, подставим полученное вместо левой части равенства (1.8):
λ |
|
2t |
= c |
t |
(1.9) |
||||
x2 |
τ |
||||||||
|
|
|
|
||||||
или |
|
|
2t |
|
|
||||
|
|
t |
= a |
, |
(1.10) |
||||
|
|
τ |
x2 |
||||||
|
|
|
|
|
|
||||
где a c 1 – коэффициент температуропроводности.
Это уравнение является линейным однородным дифференциальным уравнением второго порядка с частными производными.
Если внутри нагреваемого (охлаждаемого) тела имеется дополнительный самостоятельный источник (сток) теплоты с удельной мощностью (см. рис.1.2), то для описания процесса теплопередачи к дифференциальному уравнению прибавляется дополнительный член
t |
= a |
2t |
± |
|
. |
(1.11) |
|
|
x2 |
c |
|||||
|
|
|
|
Дифференциальное уравнение теплопроводности (1.11) устанавливает связь между временными и пространственным изменением температуры в любой точке тела и является основой для всех расчетов температурных полей.
1.4. Условия однозначности
13
Дифференциальное уравнение теплопроводности (1.11) описывает перенос тепла в самом общем виде, т.е. целый класс процессов теплопроводности внутри тела. Для того, чтобы из бесчисленного множества таких явлений выделить интересующий процесс и дать его полное математическое описание, необходимо к дифференциальному уравнению присоединить математическое описание всех частных особенностей рассматриваемого процесса.
Эти частные особенности называются условиями однозначности
ивключают в себя:
1.Геометрические условия, характеризующие форму и размеры тела, в которых протекает процесс.
2.Физические условия, характеризующие теплофизические свойства среды и тела, а также наличие внутренних источников, их знак, величину и распределение.
3.Начальные условия, характеризующие распределение температур в изучаемом теле в начальный момент времени.
4.Граничные условия, характеризующие взаимодействие рассматриваемого тела с окружающей средой.
Совокупность начальных и граничных условий называется крае-
выми условиями.
Начальные условия необходимы для рассмотрения нестационарных процессов и состоят в задании закона распределения температуры внутри тела в начальный момент времени. В общем виде начальное условие может быть записано следующим образом:
t (x,y,z,0) = f (x,y,z). |
(1.12) |
В случае равномерного распределения температуры в теле на- |
|
чальное условие упрощается: |
|
t (x,y,z,0) = t0 = const. |
(1.13) |
Граничные условия могут быть заданы несколькими способами. |
|
Граничным условием I рода задается распределение температуры |
|
на поверхности тела для каждого момента времени |
|
t (0,τ) = f (τ) . |
(1.14) |
В частном случае, когда температура на поверхности является постоянной на протяжении всего времени протекания процесса теплооб-
мена, из уравнения (1.14) имеем |
|
t (0,τ) = const. |
(1.15) |
Граничным условием II рода задается |
величина плотности |
теплового потока каждой точки поверхности тела q для любого момента времени.
14
Аналитически это можно записать следующим образом: |
|
q (0,τ) = f (τ). |
(1.16) |
В простейшем случае плотность теплового потока на поверхно- |
|
сти тела во времени постоянна |
|
q (0,τ) = const. |
(1.17) |
Граничным условием III рода задается температура окружающей среды tc(t) и закон теплообмена между поверхностью тела и средой. Граничное условие третьего рода характеризует закон теплообмена между поверхностью и окружающей средой в процессе охлаждения или нагревания тела. Для описания процесса теплообмена между поверхностью тела и средой используется закон Ньютона.
Согласно закону Ньютона количество тела, отдаваемого единицей поверхности тела в единицу времени, пропорционально разности температур поверхности тела t(0,t) окружающей среды tc(t)
q t 0, tc , |
(1.18) |
где – коэффициент пропорциональности, называемый коэффициен-
том теплоотдачи.
Коэффициент теплоотдачи характеризует интенсивность теплообмена между поверхностью тела и окружающей средой. Численно он равен количеству тепла отдаваемого (при охлаждении) или воспринимаемого (при нагревании) единицей поверхности в единицу времени при разности температур между поверхностью тела и окружающей средой, равной 1º.
Согласно закону сохранения энергии количество тепла, которое отводится с единицы поверхности тела в единицу времени вследствие теплоотдачи (1.18), должно равняться теплу, подводимому из внутренних объемов тела к единице его поверхности в единицу времени вследствие теплопроводности
|
|
t |
|
|
|
t 0,τ tc |
τ = λ |
|
|
, |
(1.19) |
|
|||||
|
|
n П |
|
|
|
где n – нормаль к поверхности тела.
Индекс "П" указывает на то, что температура и градиент относятся к поверхности тела.
Граничные условия IV рода характеризуют условия теплообмена системы тел или тела с окружающей средой по закону теплопроводности. При этом полагается, что между телами существует идеальный контакт, т.е. температуры соприкасающихся поверхностей равны
15
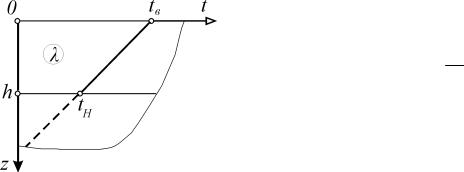
t1 |
|
П t2 |
|
П . |
(1.20) |
|
|
|
В рассматриваемых условиях имеет место равенство тепловых потоков, проходящих через поверхность соприкосновения, т.е.
|
|
t |
1 |
|
= |
|
t |
2 |
|
|
|
|
|
|
|
|
|
. |
(1.21) |
||||
n |
n |
||||||||||
1 |
|
П |
2 |
|
П |
|
|||||
Дифференциальное уравнение теплопроводности (1.11) совместно с условиями однозначности дает полную математическую формулировку конкретной задачи теплопроводности. Если перечисленные условия в совокупности определяют одно единственное явление и им удовлетворяет некоторая функция f(x,y,z,τ) , являющаяся искомым решением задачи, то в этом смысле эти условия называются условием единственности, а задача, решаемая с их помощью, называется крае-
вой задачей.
1.5. Стационарная теплопроводность
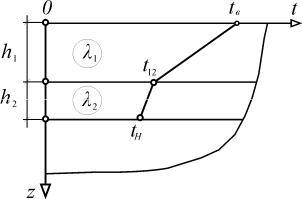
Рассмотрим неограниченную плиту толщиной h, на поверхности которой температура tв , а на подошве tн (рис.1.3).
Положим в уравнении (1.11) 0 и по условию
стационарности t = 0.
τ
|
Тогда |
имеем |
|
2t |
= 0, |
||
|
|
z2 |
|||||
|
|
|
|
|
|
|
|
|
откуда следует, что |
|
|||||
Рис.1.3. Стационарное распределение |
|
dt |
= C ; |
|
|
|
|
|
|
|
|
|
|||
температуры в термически однородной плите |
|
dz |
1 |
(1.22) |
|||
|
|
t = C1 z + C2 . |
|||||
Таким образом, следствием принятых предпосылок является |
|||||||
линейный характер зависимости температуры по координате. |
|
||||||
Для определения постоянных интегрирования С1 и С2 |
в формуле |
||||||
(1.22) располагаем граничными условиями при z = 0, t = tв ; при z = h , t = tН . С учетом этого из (1.22) получим
С2 |
= tв ; C = |
tН tв |
; |
|
|||
|
|
||||||
|
1 |
|
h |
|
|||
|
|
tН tв |
|
|
|||
t = tв |
+ |
z, или |
(1.23) |
||||
|
|||||||
|
|
h |
|
|
|
||
|
16 |
|
|
|
|
||
|
tв t |
z |
|
|
|
|
|
|
|
|
|||
|
|
|
|
= |
|
. |
|
|
|
|
|
(1.24) |
|
|
|
|
h |
|
|
|
|
||||||
|
tв tН |
|
|
|
|
|
|
|
|
||||
Вычислим количество тепла, проходящего через плиту. Согласно |
|||||||||||||
закону Фурье (1.3) имеем q= gradt = |
dt |
, где |
dt |
= C = |
tН |
tв |
. |
||||||
dz |
dz |
|
|
||||||||||
Тогда получим, что |
|
|
|
1 |
|
h |
|||||||
|
|
|
|
|
|
|
|
|
|||||
q= |
|
tв tН . |
|
|
|
|
(1.25) |
||||||
|
|
|
|
|
|||||||||
|
|
h |
|
|
|
|
|
|
|
|
|
||
В полученном уравнении отношение 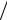 h называется коэффициентом теплопередачи плиты. Обратная её величина h
h называется коэффициентом теплопередачи плиты. Обратная её величина h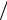 представляет собой термическое сопротивление плиты и обозначается буквой R.
представляет собой термическое сопротивление плиты и обозначается буквой R.
Обобщим полученные формулы для случая многослойной плиты. Рассмотрим двухслойную
плиту, температура поверхности tв и подошвы tн которой задана (рис.1.4). Согласно уравнению (1.25) для каждого слоя плиты имеем
q |
1 |
|
t |
|
t |
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
в |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
h1 |
|
12 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
(1.26) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
q |
t |
|
t |
H |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
h2 |
12 |
|
|
|
|
|
|
|
|
Рис. 1.4. Стационарное распределение |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
Откуда |
|
|
|
|
|
|
|
|
|
|
|
|
|
температуры в двухслойной плите |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
t |
в |
t |
|
= q |
h1 |
|
, |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
12 |
|
|
|
1 |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(1.27) |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
h |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
t |
|
t |
|
|
= q |
|
2 |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
Н |
|
|
|
|
|
. |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
12 |
|
|
|
|
|
2 |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Просуммировав левые и правые части равенств (1.27), получим |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
h2 |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
h1 |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
tв t |
|
|
|
|
+ |
|
|
(1.28) |
||||||||
|
|
|
|
|
|
|
|
|
|
|
Н = q |
|
|
2 |
. |
||||||||||||
Следовательно, |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
tв tН |
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
q= |
|
|
|
|
|
. |
|
(1.29) |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
1 |
+h |
2 1 |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
h1 1 |
|
|
|
2 |
|
|
||||||||
Или же для n – слойной плиты
17
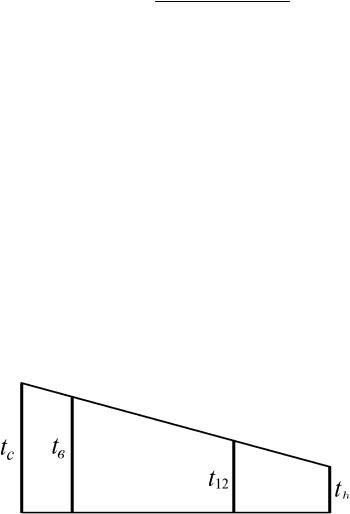
q= |
tв tН |
. |
(1.30) |
|
|||
|
n |
|
|
hiλi 1
i=1
Знаменатель уравнения (1.30) называется термическим сопротивлением n - слойной плиты.
Из системы уравнений (1.27) с учетом выражения для плотности теплового потока (1.29) можно определить температуру на стыке слоев плиты
t |
=t |
в |
|
tв tН h1λ1 |
. |
(1.31) |
|||
|
|||||||||
12 |
|
|
h λ 1 |
+h λ 1 |
|
||||
|
|
|
1 |
1 |
2 |
2 |
|
|
|
Для температуры на стыке i и i+1 слоев n - слойной плиты, следуя выражению (1.31), можно записать
i= j
tв tН hi λi 1
tj,j+1 = tв |
i=n |
i=1 |
, |
(1.32) |
|
hi λi 1
i=1
i= j
где член hiλi 1 – термическое сопротивление пакета слоев плиты
i=1
над стыком i и i+1 слоев.
При необходимости термическое сопротивление контакта между поверхностью плиты и окружающей средой учитывается членом 1 . Тогда при граничных условиях третьего рода формула (1.32) запишется следующим образом:
. Тогда при граничных условиях третьего рода формула (1.32) запишется следующим образом:
|
t |
|
|
|
|
|
|
1 |
|
i= j |
1 |
|
|
|
|
|
t |
|
|
|
+ |
h λ |
|
|
|
||||
|
|
|
|
|
|
|
|
|||||||
|
|
c |
|
|
Н |
|
α |
|
i i |
|
|
|
||
ti,j+1 = tc |
|
|
|
|
|
|
|
|
i=1 |
|
|
, |
(1.33) |
|
|
|
|
|
1 |
|
|
i=n |
1 |
|
|
||||
|
|
|
|
|
|
|
+ |
hiλi |
|
|
|
|
||
|
|
|
|
α |
|
|
|
|
||||||
|
|
|
|
|
i=1 |
|
|
|
|
|
||||
где tc – температура окружающей среды над поверхностью плиты.
|
1 |
1 |
1 |
|
h1 1 |
h2 2 |
Рис.1.5. Графическое определение стационарного
распределения температур в двухслойной плите
18

Полезно иметь в виду возможность графического определения стационарного распределения температуры в многослойной плите. Отложим последовательно вдоль на прямой термические сопротивления слоев плиты, как это показано на рис. 1.5 для двухслойной плиты. На концах полученного отрезка отложим по нормали в произвольном масштабе граничные температуры tc и tн. Выполнив очевидные из рис.
1.5построения, получим искомые температуры tв и t12 .
1.6.Критерии и числа подобия
Вматематическом выражении решения краевой задачи все входящие в него размеры величины можно сгруппировать в безразмерные комплексы. Покажем это на примере формулы (1.24) из задачи стационарной теплопроводности. Искомая температура пластины t в сочетании с температурными параметрами tв и tн образует
безразмерную независимую переменную tв t , а текущая координа- tв tН
та z, отнесенная к толщине пластины h, которая служит здесь геометрическим параметрам, представляет собой безразмерную независи-
мую переменную. Приняв обозначения Z = z ,θ = θt , получаем θ = Z. h θ0
Новые переменные θ и Z могут изменяться от 0 до 1. Преимущества безразмерной формулы (1.34) по сравнению с первоначальной (1.24) очевидны.
Вместо пяти размерных величин можно рассматривать только две: относительную температуру θ и безразмерную координату Z.
Обращаем внимание, что под параметром понимается величина, сохраняющая постоянное значение лишь в условиях данной задачи, в других же случаях она может иметь различные значения. Например: характерные размеры тела, теплофизические свойства его материала, начальная температура, коэффициент теплоотдачи и т.д.
В теории подобия различают критерии подобия и числа подобия.
Критерии подобия – это безразмерные комплексы, состоящие из параметров, заданных по условию. Примером такого типа критерия являя-
ется критерий Био (Bi= h ). В то же время безразмерный комплекс
λ
19

Фурье (Foz = aτ ) в таком виде не является критерием, а обобщенной h2
переменной или числом Фурье. Однако если по условию задачи задано некоторое характерное время, например период колебания температуры окружающей среды Т, то аналогичный комплекс aT h2 называется критерием Фурье.
Критерий Bi играет важную роль в теории теплопроводности. Он представляет собой отношение термического сопротивления теплопроводности h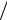 к термическому сопротивлению теплоотдачи 1
к термическому сопротивлению теплоотдачи 1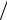 :
:
Bi= |
h |
= hλ 1 /1 1 . |
(1.35) |
|
|||
|
λ |
|
|
Остановимся на предельных случаях изменения Bi, которые позволяют существенно упрощать постановку, а следовательно, и решение задач.
1. При Bi >> 1 термическое сопротивление теплопроводности весьма велико по сравнению с термическим сопротивлением теплоотдачи. В этом случае допустимо отождествлять температуры поверхности тела и окружающей среды. Если Bi → ∞, то температура поверхности тела сразу же становится равной температуре среды. Действительно, из уравнения (1.19) следует, что
t 0,τ tc |
τ = |
λ |
|
t |
= |
αh |
|
1 |
|
t |
= |
h |
|
t |
= 0, |
α z |
|
|
|
|
|
||||||||||
|
|
|
Bi α z |
Bi z |
|||||||||||
откуда получим, что t ( 0,τ) = tc (τ).
Следовательно, в этом случае процесс теплообмена будет определяться главным образом условиями распространения тепла внутри тела, а не условиями теплоотдачи на его поверхности. Практически условие Bi →∞ можно заменить условием Bi ≥ 10. Это обстоятельство позволяет заменять сложные граничные условия III рода более простыми граничными условиями I рода.
2. При Bi << 1 термическое сопротивление теплопроводности представляет величину весьма малую по сравнению с термическим сопротивлением теплоотдачи. При этом допустимо считать, что в любой момент времени температура по всему телу имеет одинаковое значение, т.е. характеризуется большой равномерностью. В этом случае процесс теплопроводности будет определяться условиями теплообмена, происходящего на поверхности тела.
Данный случай характерен для охлаждения тонких слоев.
20

3. Возможен случай, когда Bi = 1, т.е. когда внешнее и внутреннее термическое сопротивление одного порядка. Поэтому ни тем ни дру-гим пренебречь нельзя и задачу следует рассматривать в полной постановке.
Критерий Фурье выражает определение соответствия между темпом изменения условий в окружающей среде и темпом перестройки температурного поля внутри тела. Этот критерий имеет смысл обобщенного времени, и поэтому его можно назвать критерием гомохронности, т.е. однородности по времени. Если для двух тел
отношение h2 |
a |
имеет одно и то же значение, то для них гомохрон- |
|
|
ность переходит в синхронность.
Критерий Предводителева равен максимальной производной от относительной температуры окружающей среды по относительному времени, характеризуемому критерием гомохронности Фурье.
|
dt |
c |
|
|
Pd= |
|
. |
(1.37) |
|
|
|
|||
|
|
|
|
|
d Fо max |
|
|||
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
d |
|
tc τ |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
ωh |
|
||||||
Если |
tc τ = tmax cosωτ, |
то |
Pd= |
|
tmax |
|
|
= |
|
. |
|||
|
|
|
|
|
|
|
|||||||
|
|
|
d |
τh 2 |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(1.38) |
|
|
|
|
|
|
|
max |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Таким образом, критерий Предводителева выражает соответствие |
|||||||||||||
между скоростью изменения температуры окружающей среды и скоростью температурного поля внутри тела.
1.7. Теплофизические свойства материалов
Совокупность свойств материала, характеризующих его реакцию на процессы теплообмена со средой, называется теплофизическими. Основными расчетными характеристиками теплофизических свойств материала являются коэффициент теплопроводности λ, коэффициент температуропроводности а и объемная теплоемкость С.
Эти характеристики связаны между собой соотношением
λ = а С . (1.39)
Производной основных теплофизических характеристик является коэффициент тепловой активности материала
в = λC . |
(1.40) |
21 |
|
