1472

Федеральное агентство по образованию Сибирская государственная автомобильно-дорожная академия

(СибАДИ)

Т.Е. Болдовская

ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИИ ОДНОЙ ДЕЙСТВИТЕЛЬНОЙ ПЕРЕМЕННОЙ

Сборник задач

Омск Издательство СибАДИ

2008

2

Ответы………………………………………………………………………………. 74 Библиографический список……………………………………………………….. 79

3

Введение

Сборник задач предназначен для студентов инженерно-технических специальностей, изучающих курс интегрального исчисления функции одной действительной переменной.

Пособие содержит теоретический материал, который сопровождается достаточно подробно рассмотренными примерами, задачами и иллюстрируется на рисунках. Задачи подобраны так, чтобы в процессе ознакомления с их решениями читатель мог самостоятельно овладеть основными методами решения задач интегрального исчисления. В конце задачника приведён типовой расчет, что позволит студенту приобрести практические навыки и научиться применять их в своей инженерной деятельности.

4

Глава 1. НЕОПРЕДЕЛЁННЫЙ ИНТЕГРАЛ

§ 1. Непосредственное интегрирование

Функция F x называется первообразной для функции f x , если

F x f x .

Любая непрерывная функция f x имеет бесконечное множество первообразных, которые отличаются друг от друга постоянным слагаемым.

Совокупность всех первообразных F x С, где С − произвольная постоянная, называется неопределённым интегралом и обозначается

f (x)dx F(x) C.

Основные свойства неопределённого интеграла

Таблица простейших интегралов

5

Окончание таблицы

Решение: 1) Разделим почленно числитель на знаменатель; в результате подынтегральная функция раскладывается на слагаемые, каждое из которых проинтегрируем:

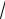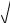8x1/2 ln x C 6 x2 x 66x5 8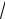x ln x C.

5

2) Прибавляя и вычитая в числителе подынтегральной функции число 4, получим

3) Возведём в квадрат подынтегральную функцию и проинтегрируем каждое слагаемое, имеем

6

4) Здесь следует воспользоваться тригонометрической формулой

1 ctg2x 1 . sin2 x

Откуда получаем

ctg2xdx sin12 x 1 dx sindx2 x dx ctgx x C.

5) Воспользуемся свойством 5 неопределённого интеграла, где

ucosx, имеем

cos3 xd cosx (cosx)3 1 C cos4 x C. 3 1 4

Применяя основные правила и формулы интегрирования, найти следующие интегралы:

7

§2. Интегрирование способом подстановки

Замена переменной в неопределённом интеграле производится с помощью подстановок двух типов:

1) x t , где t − новая переменная; t − непрерывно дифференцируемая функция. В этом случае формула замены переменной имеет вид

f x dx f (t) (t)dt .

Функцию t стараются выбрать таким образом, чтобы правая часть формулы приобрела более удобный для интегрирования вид.

2) t (x), где t − новая переменная. Тогда формула замены переменной приобретает вид

знаком дифференциала будет стоять аргумент 2x подынтегральной функции sin2x. Так как d 2x 2dx, то

8

5) Используем подстановку t 3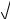x . Следовательно,

3sin3x C.

6)Применим подстановку t 1 , имеем

9