
1472
.pdf
6. x a,b |
|
|
b |
b |
|
|
f x g x f x dx g x dx. |
|
|||||
|
|
f (x) |
a |
a |
на a,b , то на этом |
|
7. Если функция |
непрерывна |
отрезке |
||||
|
|
|
|
|
b |
c a,b |
существует |
точка |
c, |
такая |
что |
f (x)dx f (c)(b a), |
|
a
(теорема о среднем).
Для вычисления определенного интеграла от функции y f (x) в том случае, когда можно найти соответствующий неопределённый интеграл F(x), служит формула Ньютона-Лейбница:
b |
|
f x dx F b F a , |
(9) |
a
где F x f x .
Замена переменной в определённом интеграле
b
Пусть для вычисления определённого интеграла f (x)dx от
a
непрерывной функции(t) и её производная a ( ) и b ( ), то
сделана подстановка x (t). |
Если функция |
|
, , причём |
(t) непрерывны на отрезке |
|
справедлива формула |
|
b |
f (x)dx |
|
|
(10) |
|
|
|
||||
f (t) (t)dt. |
|||||
a |
|
|
|
|
Интегрирование по частям в определённом интеграле
Интегрирование по частям в определённом интеграле осуществляется по формуле
|
|
|
|
|
b |
|
|
|
|
b |
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
u(x)dv u(x)v(x) |
v(x)du, |
|
|
|
|
(11) |
||||||||||
|
|
|
|
|
a |
|
|
|
|
a |
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
где u(x) и v(x) непрерывно дифференцируемы на a,b . |
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
2 |
|
|
4 |
|
|
|
|
e2 ln xdx |
|
||
|
Вычислить интегралы: 1) 5x4dx, 2) |
(3x ex/4)dx, 3) |
|
|
, |
||||||||||||||||
|
x |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
1 |
|
|
0 |
|
|
|
|
e |
|
||
8 |
xdx |
|
2ln2 |
dx |
|
|
|
e ln x |
|
|
|
|
|||||||||
4) |
|
|
|
, 5) |
|
|
|
|
, 6) |
xcosxdx, 7) |
|
|
|
|
|
dx. |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
x 1 |
|
ex 1 |
|
x |
|
|
|
|||||||||||||
3 |
|
|
ln2 |
|
0 |
|
|
1 |
|
|
|
|
|
|
|||||||
30

Решение: 1) По формуле Ньютона-Лейбница
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
25 |
15 32 1 31. |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5x4dx 5 x4dx x5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
2) На основании формулы (9) находим |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3x |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
(3x ex/4)dx |
|
|
|
|
|
4ex/4 |
|
(24 4e) (0 4) 28 4e. |
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
3) |
e2 lnxdx |
|
e2 |
lnxd(lnx) |
(lnx)2 |
|
e2 |
|
|
|
|
(lne2)2 |
|
|
|
|
(lne)2 |
|
|
|
|
|
|
|
|
|
|
1 |
|
3 |
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
. |
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
e |
|
|
|
|
|
|
|
|
|
e |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
e |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
2 |
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
4) Введем новую переменную, |
|
|
полагая |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
Отсюда |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
x 1 |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
находим t2 x 1, |
|
2tdt dx. При x 3 |
имеем t |
|
|
|
|
|
|
|
|
|
2; при x 8 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
3 1 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
имеем |
|
t |
|
|
|
|
|
|
|
3. |
Используя |
|
|
|
|
|
|
|
формулу |
|
|
|
замены |
|
|
|
|
переменной, |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
8 1 |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
получим |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
8 |
|
xdx |
3 |
t |
2 |
1 |
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t |
3 |
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
2 |
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
2tdt |
2 t |
2 |
1dt |
2 |
|
|
|
|
|
|
|
t |
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
10 |
. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
t |
|
|
3 |
|
|
|
|
|
|
2 |
3 |
|
|
3 |
|
3 |
|
2 |
3 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
3 |
|
|
x 1 2 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2tdt |
. |
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
5) |
|
Полагаем |
t |
ex 1 |
. |
|
|
Тогда |
|
x ln1 t2 |
|
|
, |
dx |
|
|
Если |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
x ln2, то t 1; если x 2ln2, то t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 t2 |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
3 |
. Следовательно, |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
2ln2 |
dx |
|
|
|
|
|
|
|
|
|
|
|
2tdt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2arctgt |
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t(1 t2) |
1 t2 |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
ln2 |
|
|
|
ex 1 |
|
1 |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 4 |
|
6 |
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
6) |
|
|
Положим |
|
|
u x, |
|
|
dv cosxdx. |
Тогда |
|
|
|
|
du dx, |
|
v sinx. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Применяя формулу интегрирования по частям, найдём |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
cos cos0 2. |
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
xcosxdx xsinx |
|
0 |
|
sinxdx sin 0sin0 cosx 0 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
7) Положим u lnx, |
dv |
|
, откуда du |
, |
v 2 |
|
|
|
|
|
. Тогда |
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
x |
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
e |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
e |
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
ln |
x |
|
dx 2 |
|
x |
ln x 1e 2 |
|
|
x |
|
dx |
2 |
|
e |
lne 2 |
|
1ln1 4 |
|
x |
1e |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
1 |
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
2
 e (4
e (4
 e 4) 2(2
e 4) 2(2 
 e).
e).
31

Вычислить определённые интегралы:
16
127. 
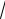 xdx.
xdx.
1
/6
130.sin3xdx.
0
133. |
/4 |
|
dx |
|
|
|||
/6 |
|
|
|
|
|
|||
sin2 x |
|
|
|
|
||||
ctgx |
|
|||||||
136. |
ln3 |
|
exdx |
. |
|
|||
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|||
|
e2x 1 |
|
||||||
|
ln2 |
|
|
|
||||
128.
131.
. 134.
137.
8 |
|
|
|
|
|
1 |
|
|
|
|
||||||||||||
|
|
4x |
|
|
|
|
|
|
|
|
dx. |
129. |
||||||||||
|
3 |
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
2 |
||||||||||||||||||
1 |
|
3 |
|
|
x |
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||
|
/2 |
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
cos3xcos5xdx. |
132. |
||||||||||||||||
/2 |
|
|
|
|
|
|
|
|
|
|
||||||||||||
4 |
|
|
|
|
|
|
|
dx |
|
|
. |
|
|
|
|
135. |
||||||
1 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
(1 2x)2 |
|
|
|
|
||||||||||||||||||
|
|
|
3 |
|
|
|
/4 arcsinx |
138. |
||||||||||||||
2 |
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dx . |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
1 x2 |
|
|
|
|||||||||||||||||
|
3 |
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
e2 2 |
|
|
|
5 7x |
||||||||
|
|
x |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
dx. |
|
|
|
|
|
|
|
x |
|
|
||||
1 |
|
|
|
|
|
|
|
|
|
|
||
4 |
|
|
|
|
|
|
dx |
|
|
|
||
3 |
|
|
|
|
|
. |
|
|||||
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|||||
|
64 x2 |
|
||||||||||
4 |
|
|
|
|
|
|
|
|
||||
1/2 |
3x dx |
|
|
|
||||||||
1/2 |
|
. |
|
|
|
|||||||
1 9x |
|
|
|
|||||||||
/ 2
sin3 xcos4 xdx.
0
99dx
139.153 
 x 1.
x 1.
5
142. xexdx.
0
0
145. arccosxdx.
1
3/2 |
|
|
|
1 x2dx. |
|||
140. |
|||
0 |
|
|
|
/2
143.(x 1)cosxdx.
0
2
146.(1 x)sin xdx.
2
3 |
|
|
dx |
|
|
|
141. |
|
|
|
. |
||
|
|
|
||||
|
||||||
|
|
x2 |
x2 9 |
|
|
|
|
3 |
|
|
|||
3
 e
e
144. x2 ln xdx.
1
0
147. (2x 3)e xdx.
1
§ 2. Площадь плоской фигуры
Площадь криволинейной трапеции, ограниченной непрерывной кривой y f (x), двумя прямыми x a и x b и отрезком a x b оси ОХ (рис.1), вычисляется по формуле
|
|
b |
|
|
|
S f (x)dx, |
(12) |
|
|
a |
|
если |
f (x) 0 |
на отрезке a,b ; |
|
|
|
b |
|
|
|
S f (x)dx, |
(13) |
|
|
a |
|
если |
f (x) 0 |
на отрезке a,b . |
|
32

Y
y f (x)
S
О |
a |
b |
X |
|
|
Рис. 1 |
|
Формулы (12) и (13) можно объединить в одну:
|
b |
|
|
|
||||
|
S |
|
f x |
|
dx. |
|
|
(14) |
|
|
|
|
|
||||
|
a |
|
|
|
|
|
|
|
Площадь фигуры, ограниченной двумя непрерывными кривыми |
||||||||
y1 f1(x) и |
y2 f2(x) и двумя прямыми |
x a |
и x b, |
где |
||||
f1(x) f2(x) |
на отрезке a,b , находится по формуле (рис.2) |
|
||||||
|
b |
|
|
|
||||
|
S f1 x f2 x dx. |
|
|
(15) |
||||
a
Y
 y f1(x)
y f1(x)
S
y f2(x)
О |
a |
b |
X |
|
|
Рис. 2
33

Если |
кривая |
|
задана |
параметрическими |
уравнениями |
||||
x x t , |
y(t) 0, |
t , то площадь криволинейной трапеции, |
|||||||
|
|||||||||
y y t , |
|
|
|
|
|
|
|
x b и отрезком a,b |
|
ограниченной этой кривой, прямыми x a |
и |
||||||||
оси ОХ, выражается по формуле |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
(16) |
|
|
|
|
|
|
|
|
|
||
|
|
|
S y t x t dt, |
|
|
||||
где a ( ), b ( ). |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|||
Площадь криволинейного сектора, ограниченного кривой r r |
|||||||||
и двумя |
полярными |
радиусами |
1 |
и |
2 |
(где 1 2 ), |
|||
вычисляется по формуле |
2 |
|
|
|
|
||||
|
|
|
S |
1 |
r2 d . |
|
(17) |
||
|
|
|
|
|
|||||
|
|
|
|
|
|||||
|
|
|
2 |
1 |
|
|
|
|
|
Вычислить площади фигур, ограниченных следующими линиями:
1) |
параболой y x2 1, прямыми |
x 1, |
x 2 и осью |
|||
абсцисс; |
|
1 |
|
|
|
|
2) |
ветвью гиперболы y |
, прямыми x 6, |
x 2 и осью |
|||
x |
||||||
|
|
|
|
|
||
абсцисс;
3)параболой y x2 4x и прямой x y 4 0;
4) |
x 3(t sint), |
и осью абсцисс; |
одной аркой циклоиды |
||
|
y 3(1 cost) |
|
5)лемнискатой r 
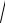 cos2 .
cos2 .
Решение: 1) На основании формулы (12) получим (рис. 3)
2 |
2 |
x3 |
2 |
8 |
|
|
|
|
1 |
|
|
|
||||
S (x |
|
1)dx |
|
x |
|
|
|
2 |
|
|
|
|
|
1 |
6 |
(кв. ед.). |
|
3 |
3 |
3 |
|||||||||||||
1 |
|
|
1 |
|
|
|
|
|
|
|
|
|||||
34

Y
y x2 1
-1 О 2 |
Х |
Рис. 3
2) На отрезке 6, 2 функция f(x) 1 отрицательна (рис. 4). x
Поэтому воспользуемся формулой (13):
2 |
1 |
dx ln |
|
|
|
2 |
|
|
|
S |
|
x |
|
(ln2 ln6) ln3 (кв. ед.). |
|||||
|
|||||||||
6 x |
|
|
|
|
6 |
|
|
||
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
Y |
|
|
|
|
-6 |
|
|
|
|
-2 |
|
|
|
|
|
|
|
|
|
О |
X |
|
Рис. 4
35

3) Найдём абсциссы точек пересечения графиков данных
y x2 4x,
функций (рис. 5). Для этого решаем систему уравнений
y x 4.
Y
-4 |
1 |
X |
-4
Рис.5
Откуда находим x1 4, x2 1. Площадь фигуры определяем по формуле (15):
|
1 |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
3x |
2 |
|
x |
3 |
1 |
|
|
S (x 4) (x2 4x)dx (4 3x x2)dx 4x |
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||
4 |
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
2 |
|
3 |
4 |
|
|||||
|
3 |
|
1 |
|
|
|
64 |
|
|
125 |
(кв. ед.). |
|
|
|
|
|
|
|
|
|
|
|||||
4 |
|
|
|
|
|
16 24 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
2 |
|
3 |
6 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
4) При изменении x от 0 до 6 параметр t изменяется от 0 до 2 |
||||||||||||||||||||||||||
(рис.6). Находим |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
x (t) 3(1 cost) и по формуле (16) получаем |
|
|
||||||||||||||||||||||||
2 |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
||
S 3(1 cost)3(1 cost)dt 9 |
(1 cost)2dt 9 1 2cost cos2 t dt |
|||||||||||||||||||||||||
0 |
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
0 |
|
2 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
1 cos2t |
|
|
3 |
|
sin2t |
|
|
|
|
|
|
|
||||||||
9 1 2cost |
|
|
|
dt 9 |
|
|
t 2sint |
|
|
|
27 (кв.ед.). |
|||||||||||||||
2 |
|
|
4 |
|
||||||||||||||||||||||
0 |
|
|
|
|
|
|
|
|
2 |
|
0 |
|
|
|
|
|
|
|||||||||
0 |
6 |
Рис.6
36

5) Изменению полярного угла от 0 до соответствует четверть
4
искомой площади (рис. 7).
Рис.7
По формуле (17) находим
|
1 /4 |
/4 |
||
S 4 |
|
cos2 d sin2 |
1 (кв.ед.). |
|
2 |
||||
|
0 |
0 |
||
Найти площади фигур, ограниченных линиями:
148.y 4x; x 3; x 1; y 0.
149.2x y 3 0; x 0; y 0; x 4.
150.y e 2x ; x 1; x 1; y 0.
2
151.y arcsin x; y /4; y /3; x 0.
152.y 2x; y 5x; x 2; x 6.
153.y 3; x y 4 0.
x
154.y 8x x2; y x2 18x 12.
155.y 6x2; y 2x3.
156.x 4cost,y 6sint.
x 8cos3 t,
y 8sin3 t.
158.r 2a(1 cos ).
159.r asin3 .
160.r2 a2 sin4 .
37

§ 3. Длина дуги кривой
Если кривая на плоскости задана уравнением y f (x), то длина дуги этой кривой, заключённой между точками с абсциссами x a и x b, находится по формуле
|
|
b |
|
|
|
|
|
|
|
|
f 2 x dx . |
|
|
||
|
|
l |
1 |
|
(18) |
||
В том |
случае, |
a |
кривая |
задана |
параметрическими |
||
когда |
|||||||
уравнениями |
x x t , |
|
и |
y(t) |
− |
непрерывно |
|
|
(x(t) |
||||||
|
y y t , |
|
|
|
|
|
|
дифференцируемые функции), то длина дуги кривой, соответствующей монотонному изменению параметра t от до , вычисляется по формуле
|
x 2 t y 2 t dt. |
|
l |
(19) |
Если кривая задана в полярных координатах r r( ), то длина дуги кривой, соответствующей монотонному изменению полярного угла от 1 до 2, находится по формуле
|
2 |
|
|
|
|
l |
r2 r 2d . |
(20) |
|||
|
|||||
|
1 |
|
|
|
|
Найти длину дуги кривой:
1) y ex/2 e x/2, 0 x 2;
2) x 3(t sint), |
0 t ; |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
y 3(1 cost), |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
3) r a(1 cos ). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
||||
Решение: 1) |
|
Дифференцируя, |
находим |
y |
(ex/2 e x/2), |
||||||||||||||||||
|
|
|
|||||||||||||||||||||
откуда |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
ex /2 e x/2 |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ex 2 e x |
|
|
|||||||
|
|
1 |
1 |
(ex 2 e x ) |
|||||||||||||||||||
|
1 f 2(x) |
||||||||||||||||||||||
|
|
4 |
|
|
|
||||||||||||||||||
|
|
|
|
|
4 |
|
|
|
|
|
2 |
|
|||||||||||
и, следовательно, по формуле (18) имеем |
|
|
|
|
|
|
|
|
|
||||||||||||||
2 |
e |
x /2 |
e |
x /2 |
|
|
|
|
|
|
1 |
|
|
|
|||||||||
|
l |
|
|
|
dx ex /2 e x/ 2 02 e |
. |
|||||||||||||||||
|
|
|
|
2 |
|
|
|||||||||||||||||
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
e |
|||||||||
38

|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
2) Так как x (t) 3(1 cost) |
, y |
(t) 3sint, то |
||||||||||||||||
|
|
|
|
|
|
|
3 |
|
|
6sin |
t |
. |
||||||
|
x 2(t) y 2(t) |
|
9(1 cost)2 |
|
9sin2 t |
|||||||||||||
|
|
2(1 cost) |
||||||||||||||||
|
|
|
||||||||||||||||
По формуле (19) получим |
|
|
|
|
|
|
|
|
2 |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
t |
|
|
|
t |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
l 6 sin |
|
|
dt 12cos |
|
|
|
|
|
12cos |
|
12cos0 12. |
||||||
|
2 |
2 |
|
|
2 |
|||||||||||||
0 |
|
|
|
0 |
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|||||||||
3) Кардиоида симметрична относительно полярной оси. Изменяя полярный угол от 0 до , мы получим половину длины кардиоиды. Так как r asin , следовательно,
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
l 2 |
a(1 cos ) 2 |
asin 2d 2a |
2(1 cos ) |
d 4a cos |
d |
|||||||||
2 |
||||||||||||||
0 |
|
|
|
|
|
|
|
0 |
0 |
|
||||
8asin |
|
|
|
8asin |
|
8asin0 8a. |
|
|
|
|
||||
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
||||||
|
2 |
|
|
0 |
2 |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|||||||
Вычислить длины дуг кривых:
161.y2 x3, 0 x 5.
162.y lnsin x, x .
|
2y x2 |
|
|
|
3 |
2 |
||||
163. |
3 между точками пересечения с осью ОХ. |
|||||||||
|
|
|
t3 |
|
|
|
|
|
||
164. |
x |
|
|
t, |
1 t 4. |
|||||
3 |
||||||||||
|
|
|
|
2 |
2, |
|
|
|||
|
y t |
|
|
|
|
|||||
|
|
x |
t |
6 |
, |
|
|
|
||
|
|
|
|
|
|
|||||
165. |
|
|
между точками пересечения с координатными осями. |
|||||||
|
|
|
6 |
t4 |
||||||
|
|
|
|
|
|
|
|
|
||
|
y 2 |
4 |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
166. r 5sin .
167. r sin3 , 0 . 3 4
39
