Задание № 3
Рассматривается так называемая
замкнутая СМО, состоящая из
одинаковых устройств, каждое из которых
в любой момент может выйти из строя и
потребовать обслуживания для устранения
неисправности. Интенсивность простейшего
потока неисправностей каждого устройства
равна
.
Количество каналов обслуживания,
устраняющих неисправности равно
.
Каждый канал обслуживает одно устройство.
Поток обслуживания каждым каналом
простейший с интенсивностью
.
Если в момент выхода устройства из строя
все каналы заняты, устройство становится
в очередь на обслуживание и ждет, пока
какой либо из каналов не освободится.
Дисциплина очереди первым пришел –
первым обслуживаешься. Порядок занятия
свободных каналов – по возрастанию их
номеров.
1. Определить
переменные состояния. Составить граф
переходов и систему дифференциальных
уравнений относительно вероятностей
состояний. Используя средства программной
системы MATLAB решить эти
уравнения и оценить время переходного
процесса. Оценить (финитные) значения
вероятностей состояний и вероятности
того, что а) число неисправных устройств
в очереди не превышает
и б) число занятых каналов обслуживания
составляет не более
.
2. Средствами визуального
моделирования Simulink-Stateflow
программной системы MATLAB
составить имитационную модель СМО,
рассматривая процесс в системе как
марковский процесс. Способ продвижения
модельного времени – по особым состояниям.
Провести моделирование на интервале
времени
,
превышающем не менее чем на порядок
время переходного процесса п.1.
3. Аналогично п.2 составить
имитационную модель процесса в СМО,
основываясь на представлении
системы в понятиях
–
схемы. Провести моделирование при
заданных параметрах потоков, а также
при условии, что поток обслуживания
равномерный с параметрами
и
,
=1,…,n.
Способ продвижения модельного времени
– с постоянным шагом. Шаг
принимается примерно на 2-3 порядка
меньше среднего интервала между
поступлением заявок или средними
временами обработки заявок каналами
обслуживания.
4. Составить программу в
виде m-файла имитационной
модели СМО, основываясь на представлении
системы в понятиях
–
схемы. Способ продвижения модельного
времени – по особым состояниям. Провести
моделирование в соответствии с заданием
п.1,2 и 3.
5. Сравнить результаты аналитического моделирования (п. 1) с результатами имитационного (п.п. 2,3и 4).
Таблица исходных данных
-
a1
b1
a2
b2
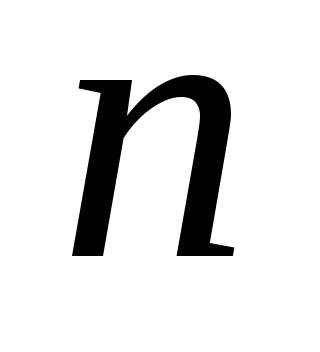
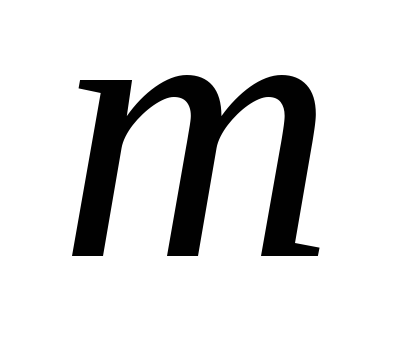
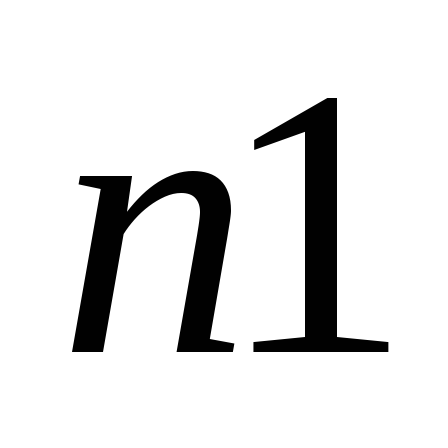
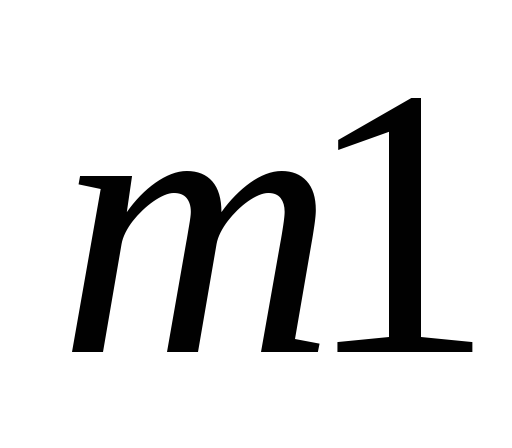
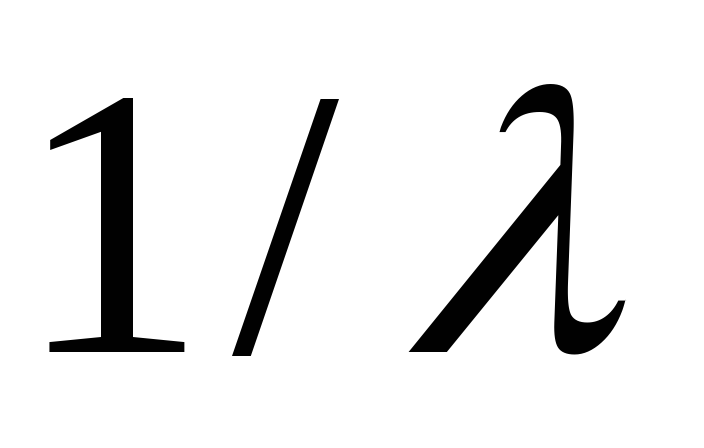
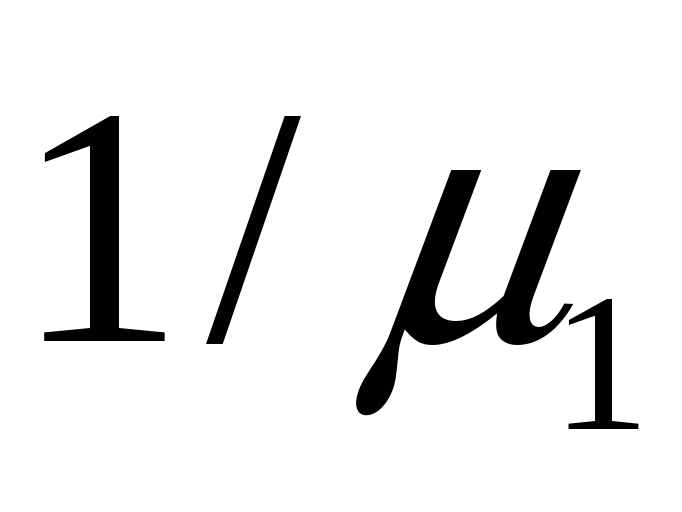
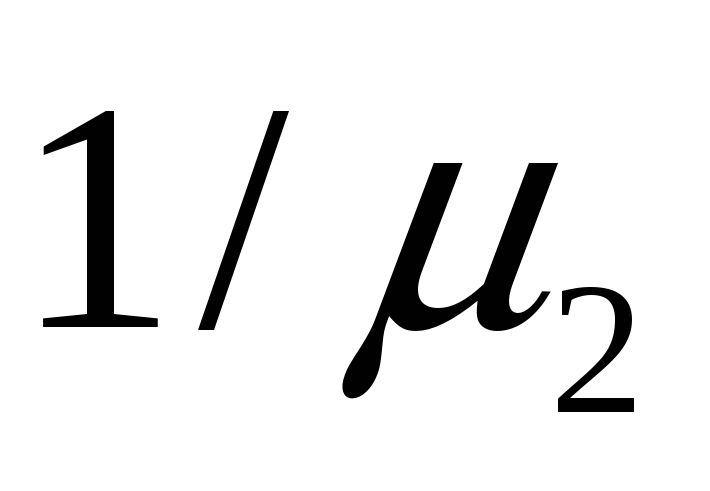
1
5
15
7
13
2
2
2
1
60
10
10
2
10
20
8
22
2
3
1
2
80
15
15
3
6
10
–
–
1
3
1
2
90
8
–
4
8
16
6
18
2
4
2
1
120
12
12