1.3. Оценки погрешности

Пусть a – точное значение некоторой величины, a* – ее приближенное значение. Абсолютная погрешность приближенного значения равна . Поскольку точное значениеa обычно неизвестно, то задача состоит в нахождении оценки абсолютной погрешности , которая удовлетворяет неравенству– оценка не должна быть меньше истинной погрешности.

Относительная погрешность определяется отношением: . Для оценки абсолютной величины относительной погрешностидолжно выполняться неравенство:

.

Значащими цифрами числа называются все цифры в его записи, начиная с первой ненулевой слева. В нормализованной системе все цифры – значащие.

Значащая цифра называется верной, если абсолютная погрешность числа не превосходит половины единицы разряда, соответствующего этой цифре.

1.4. Машинный эпсилон

Пусть имеется двоичная нормализованная система с t разрядами. Пусть точное значение числа a представляет собой бесконечную двоичную дробь с экспоненциальным множителем:

.

Пусть приближенное значение получается в результате усечения – отбрасывания всех разрядов, начиная с -го:

, –

тогда абсолютная ошибка равна

.

В нормализованной системе

.

Следовательно, относительная ошибка удовлетворяет неравенству:

.

Если вместо простого отбрасывания младших разрядов используется округление, то можно считать, что относительная ошибка в два раза меньше:

.

Отсюда следует, что точное число и соответствующее ему округленное число связаны равенством:

, где .

Число называетсямашинный эпсилон. Машинный эпсилон характеризует точность арифметики с плавающей запятой.

Машинный эпсилон определяют как наименьшее число , такое, что.

Один из вариантов оценки числа на языке пакета Mathematica:

For[ ep=1.; s=2., s>1., ep=ep/2; s=ep+1. ]; 2 ep

Исходное число ep=1. делится многократно пополам до тех пор, пока не будет нарушено условие На печать выводится удвоенный результат последнего деления.

Отметим, что в библиотеках языка Си имеются встроенные значения машинного эпсилон для формата float: FLT_EPSILON=и для форматаdouble: DBL_EPSILON=.

1.5. Погрешности вычисления значений функций

Абсолютная погрешность дифференцируемой функции , вызываемая достаточно малой погрешностью аргумента, оценивается величиной

.

Относительная погрешность оценивается величиной

.

Абсолютная погрешность дифференцируемой функции , вызываемая достаточно малыми погрешностямиаргументов, оценивается величиной

.

Относительную погрешность можно оценить по формуле:

.

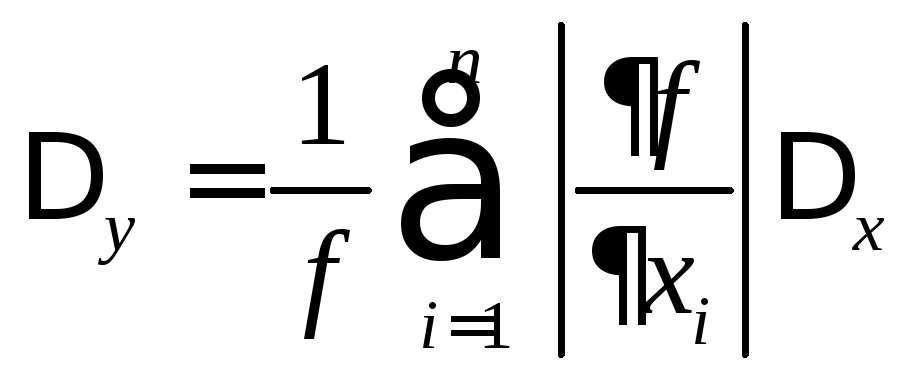Абсолютная погрешность алгебраической суммы нескольких приближенных чисел равна сумме абсолютных погрешностей слагаемых:

если , то.

При большом количестве слагаемых оценка абсолютной погрешности по этой формуле оказывается сильно завышенной, так как обычно происходит частичная компенсация погрешностей разных знаков. Если все слагаемые округлены до m-го десятичного разряда, то их погрешности оцениваются величиной . Статистическая оценка абсолютной погрешности суммы определяется по формуле:

.

Если среди слагаемых имеется одно число, абсолютная погрешность которого значительно превосходит абсолютные погрешности остальных слагаемых, то абсолютная погрешность суммы считается равной этой наибольшей погрешности.

Относительная погрешность разности двух положительных чисел больше относительной погрешности этих чисел, особенно если эти числа близки друг к другу, то есть если их разность мала по сравнению с этими числами. Это приводит к потере точности при вычитании близких чисел.

Пример 1.3. Даны два числа ис абсолютными погрешностями. Требуется оценить погрешность их разности.

Находим: ,. Относительная погрешность равна. Получаем, что разность не содержит ни одного верного знака, хотя сами числа имеют малые относительные погрешности:.