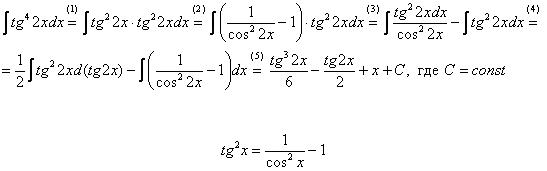
Это пример для самостоятельного решения. В образце решения дважды последовательно использована вышеупомянутая формула.
Если под степенью находится неразложимый на множители квадратный трехчлен, то решение сводится к двучлену путем выделения полного квадрата, например:
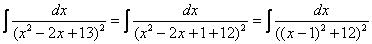 .
.
Далее следует «безболезненная» линейная замена 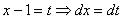 и получается знакомый интеграл
и получается знакомый интеграл
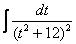 .
.
Что делать, если дополнительно в числителе есть многочлен? В этом случае используется метод неопределенных коэффициентов, и подынтегральная функция раскладывается в сумму дробей. Если такой интеграл встретится, смотрите учебник – там всё просто.
Интегрирование сложных тригонометрических функций
На уроке Интегралы от тригонометрических функций мы разобрали интеграл от тангенса в квадрате. В том примере для нахождения интеграла мы применяли тригонометрическую формулу
 .
.
Интеграл от тангенса в четвертой, пятой степени (редко в более высоких степенях) решается с помощью этой же формулы!
Пример 15 Найти неопределенный интеграл
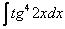 .
.
Идея решения подобных интегралов состоит в том, чтобы с помощью формулы  «развалить» исходный интеграл на несколько более простых интегралов:
«развалить» исходный интеграл на несколько более простых интегралов:
(1) Готовим подынтегральную функцию к применению формулы.
(2)Для одного из множителей используем формулу
(3)Раскрываем скобки и сразу же используем свойство линейности неопределенного интеграла.
(4)В первом интеграле используем метод подведения функции под знак дифференциала, во втором интеграле еще раз используем формулу
 , в данном случае
, в данном случае 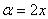 .
.
(5) Берём все три интеграла и получаем ответ.
Пример 16

Найти неопределенный интеграл
Это пример для самостоятельного решения.
Для котангенса существует аналогичная формула:
 . Полное решение и ответ в конце урока.
. Полное решение и ответ в конце урока.
Если возникли затруднения или недопонимание, следует вернуться к уроку Интегралы от тригонометрических функций. На вышеупомянутом уроке мы рассматривали универсальную тригонометрическую подстановку для решения определенного вида интегралов от тригонометрических функций. Недостаток универсальной тригонометрической подстановки заключается в том, что при её применении часто возникают громоздкие интегралы с трудными вычислениями. И в ряде случаев универсальной тригонометрической подстановки можно избежать! Рассмотрим еще один канонический пример - интеграл от единицы, деленной на синус:
Пример 17 Найти неопределенный интеграл
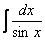 .
.
Здесь можно использовать универсальную тригонометрическую подстановку и получить ответ, но существует более рациональный путь. Приведём это решение с комментариями к каждому шагу:
(1) Используем тригонометрическую формулу синуса двойного угла
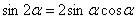 .
.
(2) Проводим искусственное преобразование: В знаменателе делим и умножаем на
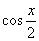 .
.
(3)По известной формуле в знаменателе превращаем дробь в тангенс.
(4)Подводим функцию под знак дифференциала.
(5)Берём интеграл.
Пример 18 Найти неопределенный интеграл
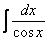 .
.
Указание: Самым первым действием следует использовать формулу приведения
и аккуратно провести аналогичные предыдущему примеру действия.
Пример 19 Найти неопределенный интеграл
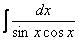 .
.
Ну, это совсем простой пример. Полные решения и ответы в конце урока.
Думаем, теперь ни у кого не возникнет проблем с интегралами:
 и т.п.
и т.п.
В чём состоит идея метода? Идея состоит в том, чтобы с помощью тождественных преобразований и тригонометрических формул организовать в подынтегральной функции только тангенсы и производную тангенса
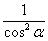 .
.
То есть, речь идет о замене:
 .
.
В Примерах 17-19 мы фактически и применяли данную замену, но интегралы были настолько просты, что дело обошлось эквивалентным действием – подведением функции под знак дифференциала.
Примечание: аналогичные рассуждения можно провести и для котангенса.
Существует и формальное правило для применения вышеуказанной замены:
Если сумма степеней косинуса и синуса – целое отрицательное число, то интеграл можно свести к тангенсам и его производной.
Для интеграла 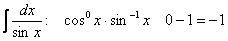 – целое отрицательное число.
– целое отрицательное число.
Для интеграла 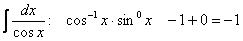 – целое отрицательное число.
– целое отрицательное число.
Для интеграла  – целое отрицательное число. Рассмотрим пару более содержательных примеров на это правило:
– целое отрицательное число. Рассмотрим пару более содержательных примеров на это правило:
Пример 20 Найти неопределенный интеграл
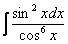 .
.
Сумма степеней синуса и косинуса 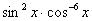 : 2 – 6 = –4 – целое отрицательное число, значит, интеграл можно свести к тангенсам и его производной:
: 2 – 6 = –4 – целое отрицательное число, значит, интеграл можно свести к тангенсам и его производной:
293
(1)Преобразуем знаменатель.
(2)По известной формуле получаем 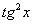 .
.
(3)Преобразуем знаменатель.
(4)Используем формулу
.
(5)Подводим функцию под знак дифференциала.
(6)Проводим замену 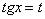 . Более опытные студенты замену могут и не проводить, но всетаки лучше заменить тангенс одной буквой – меньше риск запутаться.
. Более опытные студенты замену могут и не проводить, но всетаки лучше заменить тангенс одной буквой – меньше риск запутаться.
Далее берётся простой интеграл и проводится обратная замена.
Пример 21 Найти неопределенный интеграл
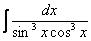 .
.
Это пример для самостоятельного решения.
Пример 22 Найти неопределенный интеграл
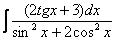 .
.
В этом интеграле изначально присутствует тангенс, что сразу наталкивает на уже знакомую мысль:
.
Пара творческих примеров для самостоятельного решения:
Пример 23 Найти неопределенный интеграл
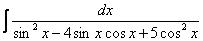 .
.
Пример 24 Найти неопределенный интеграл
294

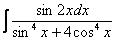 .
.
Да, в них, конечно, можно понизить степени синуса, косинуса, использовать универсальную тригонометрическую подстановку, но решение будет гораздо эффективнее и короче, если его провести через тангенсы. Полное решение и ответы в конце урока.
Переходим к заключительному пункту путешествия в мир сложных интегралов:
Интеграл от корня из дроби
Интеграл, который мы рассмотрим, встречается достаточно редко, но я буду очень рад, если единственный пример данного параграфа вам поможет.
Корнями всё начиналось, корнями и закончится. Рассмотрим неопределенный интеграл:
 , где a, b, c, d – числа. Считаем, что все эти числа и коэффициенты не равны нулю.
, где a, b, c, d – числа. Считаем, что все эти числа и коэффициенты не равны нулю.
В подынтегральной функции у нас находится корень, а под корнем – дробь, в числителе и знаменателе которой располагаются линейные функции.
Метод стар – необходимо избавиться от корня. Стар и уныл, но сейчас станет веселее, поскольку придется проводить непростую замену.
Замена, с помощью которой мы гарантированно избавимся от корня, такова:
 .
.
Теперь нужно выразить «икс» и найти, чему равен дифференциал dx. Выражаем «икс»:
Теперь найдем дифференциал:
Зачем были эти нелепые скучные телодвижения?
Мы вывели готовые формулы, которыми можно пользовать при решении интеграла вида
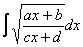 !
!
Формулы замены таковы:
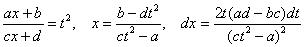 .
.
Заключительный пример:
Пример 25 Найти неопределенный интеграл
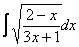 .
.
Проведем замену:
 .
.
В данном примере: a =-1, b = 2, c = 3, d = 1. Тогда для dx имеем:
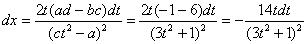 .
.
Таким образом:
 .
.
Такой интеграл, кстати, уже фигурировал в Примере 13. Интегрируем по частям:
Проведем обратную замену. Если изначально
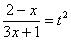 ,
,
то обратно:
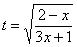 .
.
Преобразуем далее:
.
Некоторым страшно, а я это продифференцировал, ответ верный! Иногда встречаются интегралы вида
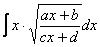 ,
, 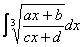 ,
,
но это нужно быть либо слишком умным, либо попасть под раздачу.
Идея та же – избавиться от корня, причем во втором случае, как все догадались, следует проводить подстановку
 .
.
и самостоятельно выводить, чему будет равняться дифференциал dx. Теперь вам практически любой интеграл по силам, успехов!
Решения и ответы:
Пример 2: Решение:
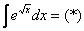 .
.
Проведем замену:
Интегрируем по частям:
297
Пример 3: Ответ:
 .
.
Пример 4: Ответ:
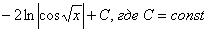 .
.
Пример 6: Решение:
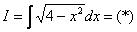 .
.
Интегрируем по частям:
Таким образом:
В результате:
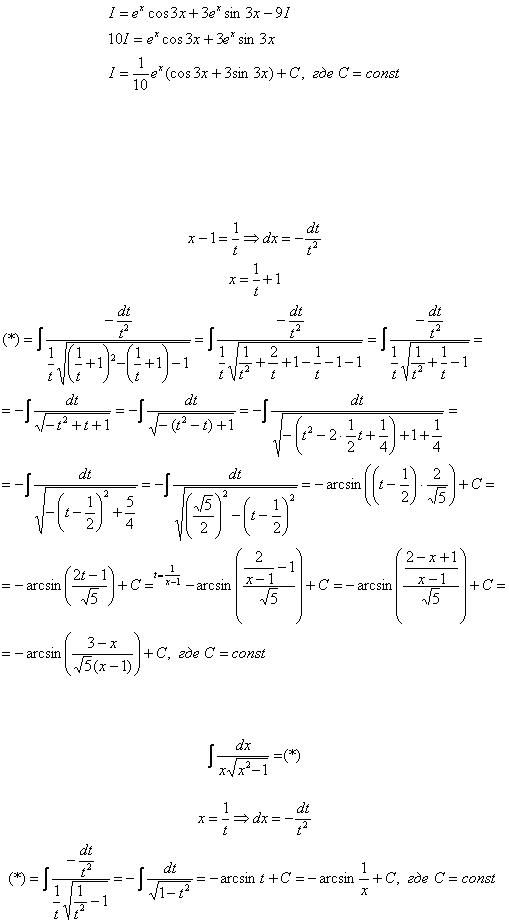
Пример 8: Решение:
Дважды интегрируем по частям и сводим интеграл к самому себе:
Таким образом:
Пример 12: Решение:
Замена:
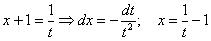 .
.
Пример 14: Решение:
Дважды используем рекуррентную формулу
Пример 16: Решение:
Пример 18: Решение:
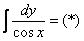 .
.

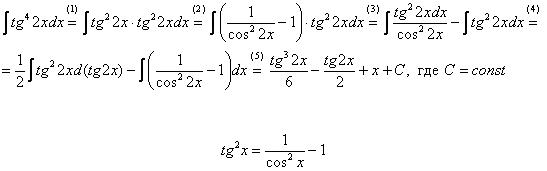


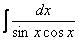 .
. и т.п.
и т.п.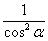 .
. .
.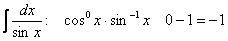 – целое отрицательное число.
– целое отрицательное число.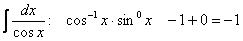 – целое отрицательное число.
– целое отрицательное число. – целое отрицательное число. Рассмотрим пару более содержательных примеров на это правило:
– целое отрицательное число. Рассмотрим пару более содержательных примеров на это правило: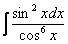 .
.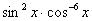 : 2 – 6 = –4 – целое отрицательное число, значит, интеграл можно свести к тангенсам и его производной:
: 2 – 6 = –4 – целое отрицательное число, значит, интеграл можно свести к тангенсам и его производной:
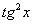 .
.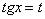 . Более опытные студенты замену могут и не проводить, но всетаки лучше заменить тангенс одной буквой – меньше риск запутаться.
. Более опытные студенты замену могут и не проводить, но всетаки лучше заменить тангенс одной буквой – меньше риск запутаться.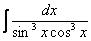 .
.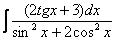 .
.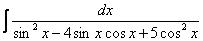 .
.
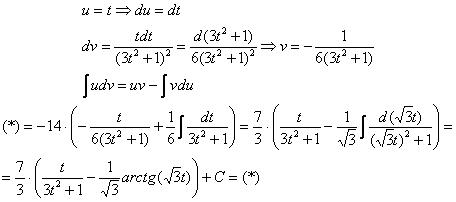

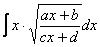 ,
, 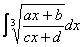 ,
, .
.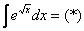 .
.
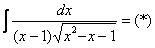 .
.

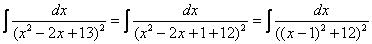 .
.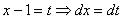 и получается знакомый интеграл
и получается знакомый интеграл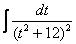 .
. .
.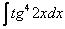 .
. «развалить» исходный интеграл на несколько более простых интегралов:
«развалить» исходный интеграл на несколько более простых интегралов: , в данном случае
, в данном случае 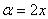 .
. . Полное решение и ответ в конце урока.
. Полное решение и ответ в конце урока.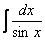 .
.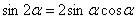 .
.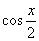 .
.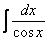 .
.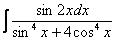 .
. , где
, где  .
.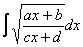 !
!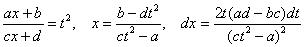 .
.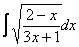 .
. .
.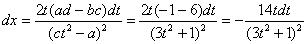 .
. .
.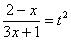 ,
,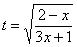 .
. .
.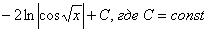 .
.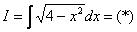 .
.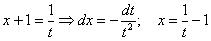 .
. .
.