
Смотрим в таблицу производных и замечаем формулы  ,
,  , то есть,
, то есть,
внашем подынтегральном выражении есть функция и её производная. Однако мы видим, что при дифференцировании косинус и синус взаимно превращаются друг в друга, и возникает вопрос: как выполнить замену переменной и что же обозначать за t – синус или косинус?! Вопрос можно решить методом научного тыка: если мы неправильно выполним замену, то ничего хорошего не получится.
Общий ориентир: в похожих случаях за t нужно обозначить функцию, которая находится
взнаменателе.
Итак, запомнили:
 .
.
Прерываем решение и проводим замену
 ;
;
 .
.
В знаменателе у нас всё хорошо, всё зависит только от, теперь осталось выяснить, во что
превратится  .
.
Для этого находим дифференциал dt:
Или, если короче:  Из полученного равенства по правилу пропорции получаем нужное нам выражение:
Из полученного равенства по правилу пропорции получаем нужное нам выражение:
 .
.
Итак:
Теперь всё подынтегральное выражение у нас зависит только от t и можно продолжать решение
Готово. Напоминаем, что цель замены – упростить подынтегральное выражение. В данном случае всё свелось к интегрированию степенной функции по таблице.
А сейчас два примера для самостоятельного решения:
Пример 12 Найти неопределенный интеграл
 .
.
Пример 13 Найти неопределенный интеграл

 .
.
Полные решения и ответы в конце урока.
Пример 14 Найти неопределенный интеграл
 .
.
Здесь опять в подынтегральном выражении находятся синус с косинусом (функция с производной), но уже в произведении, и возникает дилемма – что обозначать за t, синус или косинус?
Можно попытаться провести замену методом научного тыка, и, если ничего не получится, то обозначить за t другую функцию, но есть общий ориентир.
Общий научный ориентир: за t нужно обозначить ту функцию, которая, образно говоря, находится в «неудобном положении».
Мы видим, что в данном примере, что студент косинус «мучается» от степени, а синус – свободно так сидит, сам по себе… Поэтому проведем замену:
 .
.
Пример 15 Найти неопределенный интеграл
 .
.
Анализируем подынтегральную функцию. Что нужно обозначить за t? Вспоминаем наши ориентиры:
1)Функция, скорее всего, находится в знаменателе;
2)Функция находится в «неудобном положении».
Кстати, эти ориентиры справедливы не только для тригонометрических функций.
Под оба критерия (особенно под второй) подходит синус, поэтому напрашивается замена
 .
.
В принципе, замену можно уже проводить, но сначала неплохо было бы разобраться, а что делать с  ? Во-первых, «отщипываем» один косинус:
? Во-первых, «отщипываем» один косинус:
 .
.
Произведение  мы резервируем под наш «будущий» дифференциал dt. А
мы резервируем под наш «будущий» дифференциал dt. А  выражаем через синус с помощью основного тригонометрического тождества:
выражаем через синус с помощью основного тригонометрического тождества:
 . Проводим преобразования:
. Проводим преобразования:
Вот теперь замена: 
Готово.
Общее правило: Если в подынтегральной функции одна из тригонометрических функций (синус или косинус) находится в нечетной степени, то нужно от нечетной степени «откусить» одну функцию, а за t – обозначить другую функцию.
Речь идет только об интегралах, где есть косинусы и синусы. В рассмотренном примере в нечетной степени у нас находился косинус, поэтому мы отщипнули от степени один косинус, а за t обозначили синус.
Пример 16 Найти неопределенный интеграл
 .
.
Это пример для самостоятельного решения. Полное решение и ответ в конце урока.
Универсальная тригонометрическая подстановка
Универсальная тригонометрическая подстановка – это частый случай метода замены переменной. Её можно попробовать применить, когда «не знаешь, что делать». Но на самом деле есть некоторые ориентиры для ее применения. Типичными интегралами, где нужно применить универсальную тригонометрическую подстановку, являются следующие интегралы:
 ,
,  ,
,  ,
,  и т.д. Приведём примеры использования универсальной тригонометрической подстановки.
и т.д. Приведём примеры использования универсальной тригонометрической подстановки.
Пример 17 Найти неопределенный интеграл
 .
.
Универсальная тригонометрическая подстановка в данном случае реализуется следующим способом. Проведем замену:
 .
.
Мы используем здесь не букву t, а букву z. Это не какое-то правило, просто привычка.
Здесь удобнее находить дифференциал dx, для этого из равенства  , мы выражаем x: Навешиваю на обе части арктангенс:
, мы выражаем x: Навешиваю на обе части арктангенс:
 .
.
Справа арктангенс и тангенс взаимно уничтожаются, получаем:
 ,
,
 .
.
243
Таким образом:
 .
.
На практике можно не расписывать так подробно, а пользоваться готовым результатом:
 .
.
Последнее выражение справедливо только в том случае, если под синусами и косинусами у нас
просто «иксы», для интеграла  (о котором мы еще поговорим) всё будет несколько иначе!
(о котором мы еще поговорим) всё будет несколько иначе!
При универсальной тригонометрической подстановке синусы и косинусы у нас превращаются в следующие дроби:
 ,
,  .
.
Последние равенства основаны на известных тригонометрических формулах:
 ,
,  .
.
Итак, чистовое оформление может быть таким:
Проведем универсальную тригонометрическую подстановку:  . Тогда
. Тогда
 ,
,
 .
.
Далее, с учётом подстановки:
(1) Производим в исходном интеграле подстановки:
 ,
,  ,
,  .
.
(2)Приводим знаменатель к общему знаменателю.
(3)Избавляемся от четырехэтажности дроби, при этом  у нас сокращается. Раскрываем скобки в знаменателе, двойку в числителе выносим за знак интеграла.
у нас сокращается. Раскрываем скобки в знаменателе, двойку в числителе выносим за знак интеграла.

(4)Приводим подобные слагаемые в знаменателе.
(5)Интеграл  решается методом выделения полного квадрата. Более подробно с этим методом можно ознакомиться на уроке Интегрирование некоторых дробей. Разложение
решается методом выделения полного квадрата. Более подробно с этим методом можно ознакомиться на уроке Интегрирование некоторых дробей. Разложение
является подготовкой для осуществления вышеуказанного приёма.
(6)Выделяем полный квадрат и готовим интеграл для интегрирования.
(7)Интегрируем по табличной формуле  .
.
(8)Проводим обратную замену, вспоминая, что  . Готово.
. Готово.
Рассмотрим похожий интеграл:  .
.
Нет, решать мы его не будем, а просто поймем, как проводить замену.
Здесь тоже проводится универсальная тригонометрическая подстановка:  .
.
Обратите внимание, что аргумент под тангенсом должен быть в два раза меньше, чем под
синусом и косинусом. Формулы  ,
,  сохраняют статус-кво, а вот дифференциал будет немного другой:
сохраняют статус-кво, а вот дифференциал будет немного другой:
.
Интеграл  решается путем замены
решается путем замены  и т.д., всё точно так же, единственное отличие, дифференциал будет опять немного другой.
и т.д., всё точно так же, единственное отличие, дифференциал будет опять немного другой.
Пример 18 Найти неопределенный интеграл
 .
.
Это пример для самостоятельного решения. Полное решение и ответ в конце урока.
С помощью универсальной тригонометрической подстановки решаются и другие интегралы.
Пример 19 Найти неопределенный интеграл
 .
.
Здесь перед применением универсальной тригонометрической подстановки необходимо
понизить степени в знаменателе при помощи формул  ,
,  . Попробуйте разобраться в данном примере самостоятельно, полное решение и ответ очень близко!
. Попробуйте разобраться в данном примере самостоятельно, полное решение и ответ очень близко!
Применение универсальной тригонометрической подстановки часто приводит к длинным и трудоемким вычислениям. Поэтому на практике универсальной тригонометрической подстановки стараются избегать (если возможно). Для этого используют ряд методов и приемов, о которых можно прочитать в статье Сложные интегралы.
Решения и ответы:
Пример 2: Решение:
Используем формулу:
Пример 4: Решение:
Пример 6: Решение:
Пример 8: Решение:
Пример 10: Решение:
Пример 12: Решение:
 .
.
Проведем замену:
.
Примечание: здесь можно было сделать замену  , но гораздо выгоднее обозначить за t весь знаменатель.
, но гораздо выгоднее обозначить за t весь знаменатель.
Пример 13: Решение:
 .
.
Проведем замену:
.
.
Пример 16: Решение:
Проведем замену:
.
.
Пример 18: Решение:
 .
.
Проведем универсальную тригонометрическую подстановку:
.
Пример 19: Решение:
 .
.
Универсальная тригонометрическая подстановка:
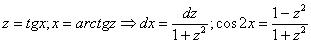 ;
;
 .
.
8.1.8. Интегрирование некоторых дробей. Методы и приёмы решения
На данном уроке мы научимся находить интегралы от некоторых видов дробей. Для успешного усвоения материала Вам должны быть хорошо понятны выкладки статей Неопределенный интеграл. Примеры решений и Метод замены переменной в неопределенном интеграле.
Как уже отмечалось, в интегральном исчислении нет удобной формулы для интегрирования дроби:
 .
.
И поэтому наблюдается грустная тенденция: чем «навороченнее» дробь, тем труднее найти от нее интеграл. В этой связи приходится прибегать к различным хитростям, о которых сейчас и расскажем.
Метод разложения числителя
Пример 1 Найти неопределенный интеграл
 . Выполнить проверку.
. Выполнить проверку.
На уроке Неопределенный интеграл. Примеры решений мы избавлялись от произведения функций в подынтегральном выражении, превращая её в сумму, удобную для интегрирования. Оказывается, что иногда в сумму (разность) можно превратить и дробь!
248

Анализируя подынтегральную функцию, мы замечаем, что и в числителе и в знаменателе у нас находятся многочлены первой степени: x и (x+3). Когда в числителе и знаменателе находятся многочлены одинаковой степени, то помогает следующий искусственный приём: в числителе
мы должны самостоятельно организовать такое же выражение, что и в знаменателе:
 .
.
Рассуждение может быть следующим: «В числителе надо организовать(x + 3), чтобы привести интеграл к табличным, но если я прибавлю к «иксу» тройку, то, для того, чтобы выражение не изменилось – я обязан вычесть такую же тройку».
Теперь можно почленно разделить числитель на знаменатель:
В результате мы добились того, чего и хотели. Используем первые два правила интегрирования:
Готово. Проверку при желании выполните самостоятельно. Обратите внимание, что  во втором интеграле – это «простая» сложная функция. Особенности ее интегрирования обсуждались на уроке Метод замены переменной в неопределенном интеграле.
во втором интеграле – это «простая» сложная функция. Особенности ее интегрирования обсуждались на уроке Метод замены переменной в неопределенном интеграле.
Кстати, рассмотренный интеграл можно решить и методом замены переменной, обозначая  , но запись решения получится значительно длиннее.
, но запись решения получится значительно длиннее.
Пример 2 Найти неопределенный интеграл
 .
.
Выполнить проверку Это пример для самостоятельного решения. Следует заметить, что здесь метод замены
переменной уже не пройдёт.
Внимание, важно! Примеры №№1,2 являются типовыми и встречаются часто.
В том числе, подобные интегралы нередко возникают в ходе решения других интегралов, в
частности, при интегрировании иррациональных функций (корней).
Рассмотренный приём работает и в случае, если старшая степень числителя больше старшей степени знаменателя.
Пример 3 Найти неопределенный интеграл
 .
.
Выполнить проверку.
Начинаем подбирать числитель. Алгоритм подбора числителя примерно такой:
1) В числителе нам нужно организовать 2x-1, но там x2. Что делать? Заключаю 2x-1 в скобки и умножаю на x, как: x(2x-1).
2) Теперь пробуем раскрыть эти скобки, что получится? Получится: (2x2-x). Уже лучше, но никакой двойки при x2 изначально в числителе нет. Что делать? Нужно домножить на (1/2), получим:
 .
.
3) Снова раскрываем скобки, получаем:
 .
.
Получился нужный x2! Но проблема в том, что появилось лишнее слагаемое (-1/2)x. Что делать? Чтобы выражение не изменилось, мы обязаны прибавить к своей конструкции это же (1/2)x:
 . Жить стало легче. А нельзя ли еще раз в числителе организовать (2x-1)?
. Жить стало легче. А нельзя ли еще раз в числителе организовать (2x-1)?
4) Можно. Пробуем:  . Раскрываем скобки второго слагаемого:
. Раскрываем скобки второго слагаемого:
 . Простите, но у нас было на предыдущем шаге (+1/2)x, а не(+x). Что делать? Нужно домножить второе слагаемое на (+1/2):
. Простите, но у нас было на предыдущем шаге (+1/2)x, а не(+x). Что делать? Нужно домножить второе слагаемое на (+1/2):
 .
.
5) Снова для проверки раскрываем скобки во втором слагаемом:
 . Вот теперь нормально: получено (+1/2)x из окончательной конструкции пункта 3! Но опять есть маленькое «но», появилось лишнее слагаемое (-1/4), значит, мы обязаны прибавить к своему выражению (1/4):
. Вот теперь нормально: получено (+1/2)x из окончательной конструкции пункта 3! Но опять есть маленькое «но», появилось лишнее слагаемое (-1/4), значит, мы обязаны прибавить к своему выражению (1/4):
 .
.
Если всё выполнено правильно, то при раскрытии всех скобок у нас должен получиться исходный числитель подынтегральной функции. Проверяем:
 Получился. Таким образом:
Получился. Таким образом:
 Готово. В последнем слагаемом мы применили метод подведения функции под дифференциал.
Готово. В последнем слагаемом мы применили метод подведения функции под дифференциал.
Если найти производную от ответа и привести выражение к общему знаменателю, то у нас получится в точности исходная подынтегральная функция
 .
.
Рассмотренный метод разложения x2 в сумму есть не что иное, как обратное действие к приведению выражения к общему знаменателю.




 .
. ,
,  ,
,  ,
,  и т.д. Приведём примеры использования универсальной тригонометрической подстановки.
и т.д. Приведём примеры использования универсальной тригонометрической подстановки. .
. .
. , мы выражаем x: Навешиваю на обе части арктангенс:
, мы выражаем x: Навешиваю на обе части арктангенс: .
. ,
, .
.



 .
.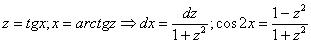 ;
; .
. .
. . Выполнить проверку.
. Выполнить проверку.

 ,
,  , то есть,
, то есть, .
. ;
; .
. .
. Из полученного равенства по правилу пропорции получаем нужное нам выражение:
Из полученного равенства по правилу пропорции получаем нужное нам выражение: .
. .
. .
. .
. .
. .
. .
. ? Во-первых, «отщипываем» один косинус:
? Во-первых, «отщипываем» один косинус: .
. мы резервируем под наш «будущий» дифференциал
мы резервируем под наш «будущий» дифференциал  выражаем через синус с помощью основного тригонометрического тождества:
выражаем через синус с помощью основного тригонометрического тождества: . Проводим преобразования:
. Проводим преобразования:
 .
. .
. (о котором мы еще поговорим) всё будет несколько иначе!
(о котором мы еще поговорим) всё будет несколько иначе! ,
,  .
. ,
,  .
. . Тогда
. Тогда ,
, .
. ,
,  ,
,  .
. у нас сокращается. Раскрываем скобки в знаменателе, двойку в числителе выносим за знак интеграла.
у нас сокращается. Раскрываем скобки в знаменателе, двойку в числителе выносим за знак интеграла. решается
решается  .
. . Готово.
. Готово. .
. .
. ,
,  сохраняют статус-кво, а вот дифференциал будет немного другой:
сохраняют статус-кво, а вот дифференциал будет немного другой: решается путем замены
решается путем замены  и т.д., всё точно так же, единственное отличие, дифференциал будет опять немного другой.
и т.д., всё точно так же, единственное отличие, дифференциал будет опять немного другой. .
. .
. ,
,  . Попробуйте разобраться в данном примере самостоятельно, полное решение и ответ очень близко!
. Попробуйте разобраться в данном примере самостоятельно, полное решение и ответ очень близко! .
. , но гораздо выгоднее обозначить за t весь знаменатель.
, но гораздо выгоднее обозначить за t весь знаменатель. .
. .
. .
. во втором интеграле – это «простая» сложная функция. Особенности ее интегрирования обсуждались на уроке
во втором интеграле – это «простая» сложная функция. Особенности ее интегрирования обсуждались на уроке  , но запись решения получится значительно длиннее.
, но запись решения получится значительно длиннее. .
. .
. .
. .
. . Жить стало легче. А нельзя ли еще раз в числителе организовать (2
. Жить стало легче. А нельзя ли еще раз в числителе организовать (2 . Раскрываем скобки второго слагаемого:
. Раскрываем скобки второго слагаемого: . Простите, но у нас было на предыдущем шаге (+1/2)
. Простите, но у нас было на предыдущем шаге (+1/2) .
. . Вот теперь нормально: получено (+1/2)
. Вот теперь нормально: получено (+1/2) .
. Получился. Таким образом:
Получился. Таким образом: Готово. В последнем слагаемом мы применили метод подведения функции под дифференциал.
Готово. В последнем слагаемом мы применили метод подведения функции под дифференциал. .
.