13. Задания с параметрами

§13. ЗАДАЧИ С ПАРАМЕТРАМИ

Квадратичная функция, расположение корней квадратичной функции Квадратичная функция формирует обширный класс задач с параметрами, разнообразных по форме и содержанию, но объединенных общей идеей – в основе их решения лежат свойства функции Для решения таких задач часто полезным оказывается применение теоремы Виета. Пример 1. Найти все значения параметра , при которых система уравнений имеет решение. Решение. Исходная система уравнений равносильна системе:

Последняя система имеет решение тогда, когда уравнение

(1)

имеет хотя бы один положительный корень.

Вычислим дискриминант квадратного уравнения (1) :

.

Рассмотрим три случая.

1)Уравнение (1) имеет только положительные корни:

125

т.е. , откуда:

. 2) Уравнение (1) имеет корни разных знаков.

Это будет тогда и только тогда, когда , т.е. , откуда .

3) Уравнение (1) имеет один положительный и один нулевой корень:

откуда Суммируя полученные результаты, имеем .

Ответ:

Пример 2. Найти все значения параметра , , при которых уравнение (2) имеет единственное решение на интервале . В ответе указать сумму целых значений параметра . Решение. (3) Нужно найти все значения параметра , при которых сис-

126

тема (3) имеет единственное решение на интервале . Рассмотрим квадратное уравнение

. (4) Его дискриминант: . 1) Если , т.е. , то уравнение (4) имеет един- ственное решение , которое является и решением сис- темы (3). Поэтому значение параметра удовлетворяет условию задачи. 2) , т.е. . Тогда уравнение (4) имеет два корня: , . Так как , то является и решением системы (3). Чтобы система (3) на интервале имела единственное решение, нужно потребовать выполнение одного из следующих условий: а) или б) . В случае а): ,

откуда: ; . В случае б): , откуда: ; . Так как , получаем, что условию задачи удов-летворяют следующие значения параметра : . Сумма целых значений из это- го множества: Ответ: .

127

Графический метод

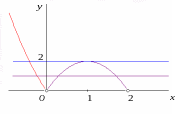
Достаточно часто встречаются задачи с параметрами, которые удобно решать графически. Пример 3. Найти значение параметра , при котором уравнение имеет ровно два решения. Решение. Обозначим . Перейдем к уравнению, равносильному исходному: Строим график функции при . Полученный график прямые семейства должны пе- ресекать в двух точках. Из рисунка видно, что это требование выполняется лишь при , т.е. . Ответ: 16.

128

Пример 4. Найти все значения параметра , при которых уравнение имеет решение на отрезке . В ответе указать количество целых значений параметра . Решение. Обозначим . Тогда

.

П оэтому требуется найти такие значения параметра , при которых уравнение имеет хотя бы один корень, принадлежащий отрезку . Построим график функции Условию задачи удовлетворяют те значения параметра , при которых среди абсцисс точек пересечения прямой с графиком вышеуказанной функции существует хотя бы одна, принадлежащая отрезку . Из рисунка видно, что это усло-

129

вие выполняется только при . Целые значения параметра : 1 ; 2; 3.

Ответ: 3.

Пример 5. Найти все значение параметра , при которых уравнение

(5)

имеет решение.

Решение.

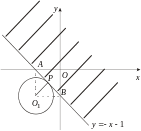
(Точки и имеют координаты: , )

Неравенство на плоскости определяет полуплоскость с границей (на рисунке эта полуплоскость заштрихована); а уравнение (6)

130

при определяет окружность радиуса с центром в точке . (При уравнение (6) определяет одну точку ; а при уравнение (6) никакого геометрического образа не определяет)

Уравнение (5) имеет решение, если радиус окружности не меньше, чем расстояние от точки до ближайшей точки на прямой .

Из прямоугольного треугольника имеем: . Итак, , т.е. , откуда: . Ответ: .

ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ 1. Найти все значения параметра , при которых система уравнений имеет три решения. ( Ответ: ) 2. Найти все значения параметра , при которых уравнение

имеет ровно три решения. В отве-

те указать сумму всех значений параметра . (Ответ: – 2)

3. Найти число целых значений параметра , при которых

уравнение имеет решение. (Ответ: 3)

4. Найти все значения параметра , при которых система

131

уравнений имеет решение. В ответе

указать наибольшее значение параметра . (Ответ: –1)

5. Найти сумму целых значений параметра , при которых

уравнение имеет только одно решение. (Ответ: 6) 6. Найти все значения параметра , при которых уравнение

имеет ровно три различных решения.

(Ответ: ) 7. Найти сумму целых значений параметра , при которых

неравенство верно при любом . (Ответ: 21) 8. Найти наименьшее значение параметра , при котором

система уравнений имеет два решения.

(Ответ: –2) 9. Найти сумму целых значений параметра , при которых

уравнение имеет два корня

разных знаков. (Ответ: 1) 10. Найти число целых значений параметра , при которых

уравнение имеет одно ре-

шение. (Ответ: 7) 11. Найти все значения параметра , при которых три корня уравнения больше, чем , а чет- вертый меньше, чем . В ответе указать , где – длина интервала значений параметра . (Ответ: 8) 12. Найти все значения параметра , при которых система

132

уравнений имеет решение. В ответе

указать наименьшее значение параметра . (Ответ: 7) 13. Найти наименьшее значение параметра , при котором не-

равенство не имеет ре-

шений. (Ответ: 0,5) 14. Найти все значения параметра , при которых система не-

равенств не имеет решений. В ответе ука-

зать наименьшее значение параметра . (Ответ: 0) 15. Найти все значения параметра , при которых система

уравнений имеет два решения. В

ответе указать число целых значений параметра . (Ответ: 1) 16. Найти все значения параметра , при которых уравнение имеет хотя бы одно решение.

(Ответ: ) 17. Найти все значения параметра , при которых уравнение

имеет единственное решение. (Ответ: ) 18. Найти все значения параметра , при которых система

уравнений имеет единственное решение. (Ответ: ) 19. Найти сумму значений параметра , при которых уравне- ние имеет единственное решение. ( Ответ: 0,8)

133

20. Найти число целых значений параметра , при которых

уравнение

имеет единственное решение. ( Ответ: 5)

21. Найти все значения параметра , при которых система

имеет хотя бы одно решение.

( Ответ: )

134