10. Стериометрия

§10. СТЕРЕОМЕТРИЯ Прямая и плоскость Основные сведения о параллельности и перпендикулярности прямых и плоскостей в пространстве: 1) если прямая, не лежащая в данной плоскости, параллельна какой-нибудь прямой, лежащей в этой плоскости, то она парал- лельна данной плоскости; 2) если плоскость проходит через прямую, параллельную другой плоскости, и пересекает эту плоскость, то линия пересечения плоскостей параллельна данной прямой; 3) если две пересекающиеся прямые одной плоскости соответственно параллельны двум прямым другой плоскости, то эти плоскости параллельны; 4) если две параллельные плоскости пересечены третьей плоскостью, то линии пересечения параллельны; 5) если прямая перпендикулярна каждой из двух пересекающихся прямых, лежащих в плоскости, то эта прямая и плоскость взаимно перпендикулярны; 6) если плоскость проходит через перпендикуляр к другой плоскости, то она перпендикулярна этой плоскости; 7) если две плоскости взаимно перпендикулярны, то прямая, проведенная в одной плоскости перпендикулярно линии пересечения плоскостей, перпендикулярна другой плоскости; 8) для того чтобы прямая, лежащая в плоскости, была перпендикулярна наклонной, необходимо и достаточно, чтобы эта прямая была перпендикулярна проекции наклонной на эту плос- кость (теорема о трех перпендикулярах). Основные формулы стереометрии а) Поверхности и объемы многогранников Обозначения: – высота, – площадь основания, – боковая поверхность, – полная поверхность, – объем. 1) Призма. ; , где – периметр сечения

93

призмы, перпендикулярного боковому ребру длины . 2) Прямая призма. , – периметр основания. 3) Прямоугольный параллелепипед ( – его измерения, –

диагональ). . 4) Куб. ; – ребро куба. 5) Пирамида. . 6) Правильная пирамида. , где – периметр основания, – апофема. 7) Усеченная пирамида. , где – площади оснований, – высота усеченной пирамиды.

б) Поверхности и объемы круглых тел Обозначение: – радиус оснований цилиндра, конуса, или радиус шара. 1) Цилиндр. . 2) Конус. , где –длина образующей. 3) Усеченный конус. , , где – радиусы оснований, – высота, – образующая усеченного конуса. 4) . ( – площадь сферической поверхности). 5) Шаровой сегмент. , где – высота сегмента. 6) Сферический сегмент. , где – высота сегмента.

94

При решении задач по стереометрии часто применяются

следующие два утверждения: 1. Если все боковые ребра пирамиды равны между собой, то они одинаково наклонены к плоскости основания. В этом случае вершина пирамиды проектируется в центр окружности, опи-санной около основания. 2. Если все двугранные углы при основании пирамиды равны между собой, то равны между собой высоты всех боковых граней. В этом случае вершина пирамиды проектируется в центр окружности, вписанной в основание пирамиды; , где – линейный угол двугранного угла при основании.

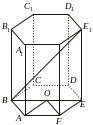Пример 1. Наибольшая диагональ правильной шестиуголь-ной призмы равна 4 и составляет с боковым ребром призмы

угол . Найти объем призмы. Решение. Наибольшая диагональ призмы: , . Объем призмы: . ; , . Площадь правильного шестиугольника: . . Ответ: 9. Пример 2. Площадь боковой поверхности цилиндра в пять

раз больше площади его основания, объем цилиндра равен . Найти площадь осевого сечения цилиндра.

95

Решение. Если – высота, а – радиус основания цилиндра, то ; площадь основания: . , т.е. . Объем цилиндра: , откуда получаем, что , следовательно, . Пусть и – центры оснований цилиндра. Через ось перпендикулярно основанию проведем сечение (осевое сечение цилиндра). Искомая площадь .

Ответ: 80.

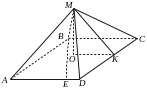Пример 3. Основанием пирамиды служит ромб, острый угол которого равен . Все двугранные углы при основании пирамиды равны . Найти объем пирамиды, если радиус окружности, вписанной в основание, равен . Решение. Пусть – ромб, лежащий в основании пирамиды , а –высота пирамиды, тогда . Проведем отрезок . Так как – высота ромба, то его длина равна диаметру вписанной окружности, т.е. . . Проведем отрезок и соединим точку с вершиной , тогда (по теореме о трех перпендикулярах), т.е. – линейный угол двугранного угла при стороне осно-

96

вания пирамиды. Тогда, и . Ответ: 1.

Пример 4. Образующая прямого кругового конуса равна и составляет с плоскостью основания угол . Найти объем вписанного в этот конус полушара, основание которого

лежит на основании конуса.

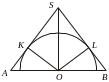Решение. Проведем осевое сечение конуса. Это равнобедренный треугольник с боковой стороной и углом при ос-новании . Центр основания конуса совпадает с центром большого круга вписанного полушара; и – точки касания конуса и полушара; – радиус полушара. . Из прямоугольного треугольника имеем: . Следовательно, . Объем полушара: .

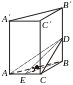
Ответ: 1152. Пример 5. Через сторону основания правильной треугольной призмы проведена плоскость под углом к плоскости основания. Определить площадь полученного треугольного

97

сечения, если объем пирамиды, отсеченной плоскостью от

призмы, равен Решение. В равностороннем треугольнике проведем высоту , тогда по теореме о трех перпендикулярах и . ;

.

Д лину стороны треугольника обозначим через .

Т 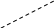огда: ; ;

. (1)

Найдем .

Из прямоугольного треугольника :

Объем пирамиды :

,

откуда ; . Подставляя найденное значение в (1) , получим :

. Ответ: . Пример 6. Правильный треугольник, сторона которого равна , вращается вокруг оси , проходящей вне его через конец

98

его стороны под острым углом в 15 к этой стороне. Определить

площадь поверхности тела вращения. Решение. Пусть - ось вращения, , , . Обозначим длину стороны треугольника через ; .

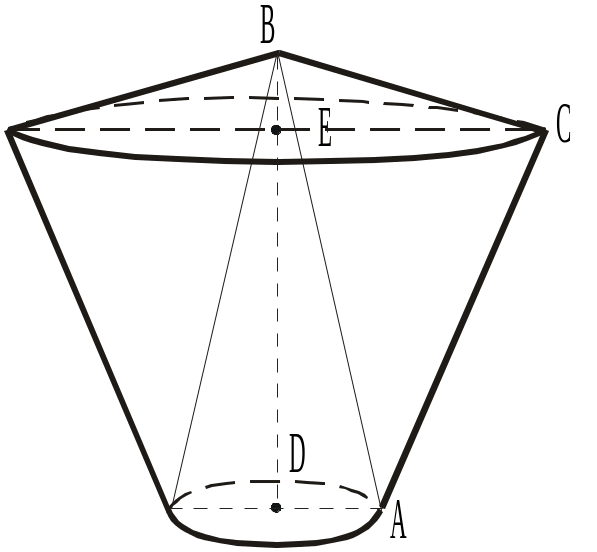Поверхность тела, образованного вращением треугольника, состоит из следующих частей:

1) боковой поверхности конуса, образованного вращением стороны ; ее площадь:

2) боковой поверхности конуса, образованного вращением стороны ; ее площадь: ;

3) боковой поверхности усеченного конуса, образованного вращением стороны ; ее площадь: , где

, .

Искомая площадь :

= Ответ: .

Пример 7. В треугольной усеченной пирамиде высота равна 10, стороны одного основания 27, 29 и 52, а периметр другого основания – 72. Вычислить объем этой пирамиды. Решение. В усеченной треугольной пирамиде периметр . Найдем площадь треугольника по формуле Герона:

99

. Треугольники и подобны с коэф- фициентом подобия .

Искомый объем:

Ответ: 1900.

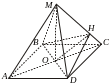Пример 8. В правильной четырехугольной пирамиде двугранный угол при боковом ребре равен . Найти площадь боковой поверхности пирамиды, если площадь ее диагонального сечения равна . Решение. – правильная пирамида, следовательно – квадрат, . Проведем , тогда (Это следует из равенства и ). Значит, – линейный угол двугранного угла при

боковом ребре ,

по условию . Кроме того , тогда – биссектриса угла . . Пусть (тогда ). Из .

100

. . Ответ: 40. ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ 1. Высота цилиндра равна 20, а диаметр основания – 80. Сече-

ние, параллельное оси цилиндра, отсекает от окружности осно-

вания дугу величиной . Найти площадь сечения. (Ответ: 800)

2. Площадь боковой поверхности конуса равна 36, расстояние от центра основания до образующей конуса равно 7. Найти объем конуса. (Ответ: 84) 3. Разверткой боковой поверхности конуса является круговой сек-

тор радиусом 5 с центральным углом . Найти объем конуса. (Ответ: ) 4. В пирамиде сечение, параллельное основанию, делит высоту в

отношении 2:3 (от вершины к основанию). Найти площадь се-

чения, зная, что она меньше площади основания на 84. (Ответ: 16) 5. В правильной треугольной пирамиде плоский угол при верши-

не равен . Высота пирамиды равна . Найти площадь бо-

ковой поверхности. В ответе указать . (Ответ: 54) 6. Боковые ребра правильной треугольной пирамиды наклонены

к основанию под углом . Найти объем пирамиды, если

101

площадь описанной около нее сферы равна . В ответе ука- зать . (Ответ: 2,25) 7. Основанием прямого параллелепипеда служит ромб со сторо-

ной 6, угол между плоскостями двух боковых граней равен . Большая диагональ параллелепипеда составляет с плос- костью основания угол . Найти объем параллелепипеда. (Ответ: 324) 8. Определить, какую часть высоты конуса (считая от вер-

шины) отсекает плоскость, параллельная основанию, если

полученные меньший конус и усеченный конус имеют рав- ные площади полных поверхностей, а образующая и радиус

основания исходного конуса равны и соответственно. В ответе указать . (Ответ: 0,8125) 9. Основанием прямой призмы служит прямоугольный тре-

угольник с гипотенузой длины и острым углом в .

Через гипотенузу нижнего основания и вершину прямого уг-

ла верхнего основания проведена плоскость, образующая с

плоскостью основания угол . Определить объем тре-

угольной пирамиды, отсеченной от призмы плоскостью. (Ответ: 0,25)

10. В равнобедренном треугольнике . Треугольник вращается вокруг оси, проходящей

через вершину и перпендикулярной . Найти объем тела вращения. В ответе указать . (Ответ: 8064)

11. Через вершину конуса и хорду основания, стягивающую ду-

гу в , проведено сечение, составляющее с плоскостью

основания угол в . Найти площадь сечения, если радиус

основания равен . (Ответ: )

12. Основание пирамиды – ромб с диагоналями и , высота

пирамиды проходит через точку пересечения диагоналей

102

ромба и равна . Найти боковую поверхность пирамиды. (Ответ: 26)

13. В конус вписан цилиндр, высота которого равна радиусу

основания конуса. Найти угол между осью конуса и его

образующей, если полная поверхность цилиндра относится

к площади основания конуса как . В ответе указать .

(Ответ: 2)