Добавил:

mayorvika Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Тульский Государственный Университет

Предмет:

Математическая составляющая естественно-научных дисциплин

Файл:

11. Векторы

.pdf

Скачиваний:

Добавлен:

11.12.2020

Размер:

495.82 Кб

Скачать

☆

§11. ВЕКТОРЫ. КООРДИНАТНЫЙ МЕТОД

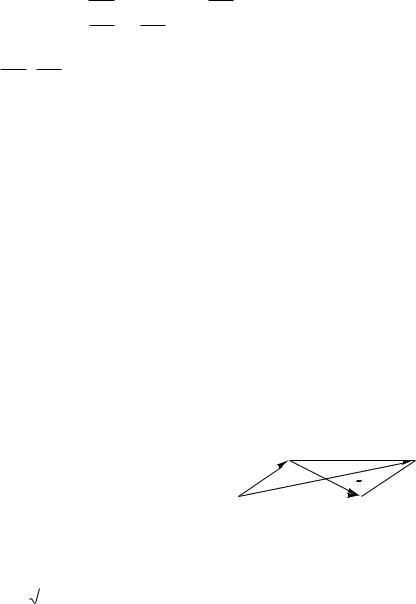
Сложение двух векторов производится по правилу параллелограмма (рис.1) или треугольника (рис.2).

a b

Рис. 1

Рис. 2

Рис.3

Разностью векторов a и b называется такой вектор c a b , что b c a ( рис.3 ).

Произведением вектора a на число называется вектор

a такой, что

1)длина вектора a равна a ;

2)векторы a и a одинаково направлены, если 0 , и противоположно направлены, если 0 .

Два ненулевых вектора a и b называются коллинеарны-

ми ( a || b ), если они лежат на параллельных прямых или на

одной прямой. a || b a b , где 0 .

Если в пространстве задана прямоугольная система коор-

динат Oxyz , i , j , k – единичные векторы координатных осей Ox, Oy, Oz соответственно, то произвольный вектор

a единственным образом представляется в виде

a ax i ay j az k ; ax , ay ,

az – координаты вектора a .

2 a

2 .

Длина вектора a :

Если известны координаты точек A и B : A x1; y1; z1 ,

B x2 ; y2 ; z2 , то AB x2 x1; y2 y1; z2 z1 . Середина С

105

отрезка AB имеет координаты: x

x1 x2

y1 y2

ax ; ay ; az ,

;by ;bz , то

Если a

ax bx ; ay by ; az bz

;

ax ; ay ; az .

Скалярное произведение векторов

Скалярным произведением векторов a и b называется

произведение длин этих векторов на косинус угла между

ними:

a b

cos .

ax ; ay ; az ,

bx ;by ;bz , то

Если

a b axbx ay by az bz .

Угол между двумя векторами

axbx a y by az bz

a b

cos

; а ,b 0 .

ax 2 a y 2 az 2

bx 2 by 2 bz 2

Если , , – углы между вектором a и осями Oх , Oу ,

Oz , соответственно, то cos 2 cos 2 cos 2 1.

Условия коллинеарности и перпендикулярности векторов

a y

a || b

a b a b 0, т.е. axbx ay by az bz 0 .

Пример 1. Даны точки А 1;7 и B 5; 1 . Найти абсциссу

х 0

точки M x;0 , если векторы

перпендику-

АМ

106

лярны.

Решение. АМ х 1; 7 , ВМ х 5;1 .

Векторы АМ и ВМ перпендикулярны тогда и только тогда, когда их скалярное произведение равно нулю:

AM BM x 1 x 5 7 0 ; х2 4х 12 0 . Корни этого

уравнения:

х1 6 ,

х2 2 . Условию задачи х 0 удовлет-

воряет только х 6 .

Ответ:

6 .

Пример 2. Найти в градусах угол между вектором 2а b и

осью

Oy , если

1;2; 3 ,

1;4;3 .

Решение. Найдем координаты вектора 2а b :

2;4; 6 ,

1;4;3 ;

поэтому

1;0; 9 .

Если

угол между вектором

2a b и осью Oy , то

cos

0 . Это означает, что 90 .

2a b

Ответ:

90 .

23 ,

Пример 3. Найти длину вектора b , если

a b

20 ,

a b

30.

Решение. Поместим начала векторов а и b в одну точку.

Тогда в параллелограмме, построенном на них, имеем:

а b

откуда

900 400

529 121;

121 11 .

Ответ: 11.

107


Пример 4. Даны четыре точки: А 1;0;2 ,			В 1;2;3 ,
С 0;2; 1 и D 4; х; у . Векторы
С 0;2; 1 и D 4; х; у . Векторы	АВ	и CD коллинеарны. Най-

ти длину вектора CD .

Решение.

2;2;1 ,

4; x 2; y 1 . Из коллинеар-

АВ

следует:

ности векторов AB

и CD

, откуда

x 2

y 1

находим, что x 6 , y 1. Тогда:

4;4;2 ,

16 16 4 6 .

Ответ: 6 .

Пример 5. Даны три последовательные вершины параллелограмма A 1; 2;3 , B 3;2;1 , C 6;4;4 . Найти сумму координат

четвертой вершины D .

Решение. Пусть D x; y; z . Так как в параллелограмме противоположные стороны параллельны и равны, то BC AD .

BC 6 3;4 2;4 1 3;2;3 , AD x 1; y 2; z 3 . Поэто-

x 1 3,
	2, откуда x 4, y 0, z 6 .	x y z 10 .
му, y 2
	3,
z 3

Ответ: 10. Пример 6. Два вектора а 2; 3;6 и b 1;2; 2 приве-

дены к одной точке. Определить координаты вектора c , направленного по биссектрисе угла между векторами a и b , если c 342 . В ответе указать большую из координат.

Решение. Пусть х , у , z – искомые координаты вектора c .

		2 x2 y 2 z 2 3		2 .
	c	2 x2 y 2 z 2 3	42	2 .		(1)

Если – угол между векторами a и b , то						– угол между
					2

векторами a и с , b и c . 108


cos			a b				2 6 12						20	.
cos							2 6 12							.
		a			b				7 3				21


cos				1 cos						1 20 / 21					1	.


	2						2		2						42

cos			a c					2x 3y			6z	.
cos												.
	2		a			c			7 3 42

(2)

(3)


cos			c b		x 2 y	2z	.	(4)
cos							.	(4)
	2	c		b	3 3 42

Учитывая (1), (2), (3), (4), получаем систему уравнений:

				6z 21,							х 3,
2х 3у							х 69 6z,
x 2 y 2z 9,							y 39 2z,				откуда y 15,
	2	y	2	z	2	378		2	24z 144	0,	z 12.
x							z

Ответ: 15. Пример 7. Катеты прямоугольного треугольника равны 3

и 4. Найти расстояние d между центрами вписанной и описанной окружностей.

Решение. Пусть в прямоугольном треугольнике OAB :

OA 3, OB 4 .

На плоскости введем прямо-

угольную систему координат

следующим образом: начало

координат разместим в вершине

прямого угла O , ось абсцисс

направим по линии OB , а ось ординат – по линии OA . Тогда

A 0;3 , B 4;0 .

Центр M описанной окружности лежит в середине гипо-

тенузы AB . Поэтому,

xA xB

0 4

2, y

yA yB

3 0

1,5 , т.е.

109

M 2;1,5 .

Центр K вписанной окружности имеет координаты:

хK r , yK	r , где r – радиус вписанной окружности.
	r	a b c	3 4 5	1

	2		2

( a OB, b OA, c AB 9 16 5 ), т.е. K 1;1 . d KM 2 1 2 1,5 1 2 1,25 ;

Ответ: 1,25

ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ

1.Даны векторы а 6; 8;52 и b 2; 4; 2 . Найти в гра - дусах угол, образуемый вектором a b с осью Oz.

(Ответ: 45)

, если

9;6; 17 ,

Найти длину вектора

1; 2;4 .

(Ответ: 13)

Отрезок AB , ограниченный точками A 1;8; 3 и

B 9; 7;2 , разделен точками M1 , M2 , M3 , M4 на пять рав-

ных частей. Найти произведение координат точки M 3 .

(Ответ: 0)

х;1;2 перпендикулярен вектору

2; у; 4 , а

Вектор

длина вектора b в два раза больше длины вектора a . Найти

x и y . В ответе указать их произведение.

(Ответ: 8)

Треугольник задан координатами своих вершин A 3; 2;1 ,

B 3;1;5 , С 4;0;3 . Найти расстояние от начала координат до

точки пересечения медиан треугольника.

(Ответ:

182

)

110

6. Даны вершины треугольника А 1; 2;4 , B 4; 2;0 и

C 3; 2;1 . Определить (в градусах) его внутренний угол при вершине B .

(Ответ: 45)

8 , а угол между

Найти длину вектора а b , если

векторами a и b равен 120 .

(Ответ: 7)

6; 8; 7,5 , образует

Вектор x , коллинеарный вектору

острый угол с осью Oz . Зная, что

50 , найти его коор-

динаты. В ответе указать меньшую из них.

(Ответ: –24)

Найти сумму длин диагоналей параллелограмма, построен-

ного на векторах

4; 1;1 и

8; 5;3 .

(Ответ: 20)

10. При каких значениях m и n точки

A( 5; 13;0), B 5; n;15

и C 7;11; m лежат на одной прямой ?

В ответе указать

m n .

(Ответ: 25)

11. Даны вершины треугольника: A 3; 1;5 , B 4;2; 5 и

C 4;0;3 . Найти длину медианы

AM .

(Ответ: 7)

12.Найти в градусах угол между диагоналями параллелограмма, построенного на векторах а 2;1; 0 и


			0; 2;1 .					(Ответ: 90)
	b		0; 2;1 .					(Ответ: 90)

13. Известно, что вектор							a b делит угол между векторами
				2;3; x и		1; x 2;4 пополам. Найти x . (Ответ: 2)
		a		2;3; x и	b	1; x 2;4 пополам. Найти x . (Ответ: 2)

14.Найти сумму координат вектора с , перпендикулярного векторам a 1; 2;1 и b 2;1; 3 и образующего с осью


Oz острый угол, если	c	2 27 .					(Ответ: 18)
				3,		1,		4,

15. Даны векторы a, b, c , причем			a		b		c

							111

a b c 0 . Найти a b b c c a .

(Ответ: – 13)

16. Даны векторы а и b , угол между которыми равен 120 . Определить длину вектора c , если c 3 a 0,5 b и

	1,		2 .
a	1,	b	2 .	(Ответ: 13 )

17.Найти длину меньшей диагонали параллелограмма, построенного на векторах a p 3q , b 5 p 2q , если из-


вестно, что		p	2	2 ,	q	3 и угол между векторами p и

	равен 45 .
q	равен 45 .					(Ответ: 15)

18.Даны три последовательные вершины параллелограмма

ABCD : А 3; 2;0 , В 3; 3;1 , С 5;0; 2 . Вычислить

скалярное произведение векторов АС и 2BD .

(Ответ: – 48)

19. Найти в градусах угол между биссектрисами углов xOz и yOz . (Ответ: 60 )

20.В трапеции ABCD с основаниями AB и CD известно, что AC AD DB DA 7 . Найти длину средней линии тра-

пеции.

(Ответ: 3,5)

21.Найти площадь треугольника ABC , если известны координаты его вершин: A 1;10 , B 2;1 , C 6; 1 . (Ответ: 15)

22.В прямоугольном треугольнике ABC длины катетов AC и

BC соответственно равны 12 и 8 . Точка K – середина медианы BD . Найти длину отрезка CK . (Ответ: 5)

23.Катеты прямоугольного треугольника равны 9 и 12. Найти расстояние между точкой пересечения биссектрис и

точкой пересечения медиан треугольника.

(Ответ: 1)

24.В правильной четырехугольной пирамиде MABCD , все ребра которой равны 1, точка E – середина ребра MD . Найдите тангенс угла между прямыми MB и AE .

(Ответ: 2 )

112

Соседние файлы в предмете Математическая составляющая естественно-научных дисциплин

#
11.12.2020163.22 Кб291. Степени и корни.pdf
#
11.12.2020740.86 Кб1810. Стериометрия.doc
#
11.12.2020495.82 Кб1711. Векторы.pdf
#
11.12.2020613.89 Кб1812. Производная функции.doc
#
11.12.2020716.8 Кб2913. Задания с параметрами.doc
#
11.12.2020513.7 Кб232. Рациональные уравнения.pdf
#
11.12.2020354.3 Кб463. Уравнения и неравенства с модулем.doc
#
11.12.2020243.71 Кб534. Иррациональные уравнения и неравенства.doc