
9. Планиметрия
.doc
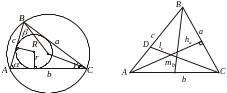 §
9. ПЛАНИМЕТРИЯ
I.
Треугольники.
§
9. ПЛАНИМЕТРИЯ
I.
Треугольники.
![]() – длины сторон треугольника
– длины сторон треугольника
![]() ,
лежащих соответственно против углов
,
лежащих соответственно против углов
![]() ;
;
![]() –
полупериметр,
–
полупериметр,
![]() и
и
![]() –
радиусы вписанной и описанной
окружностей;
–
радиусы вписанной и описанной
окружностей;
![]() –
высота, медиана и биссектриса, проведенные
к стороне
–
высота, медиана и биссектриса, проведенные
к стороне
![]() .
Площадь
треугольника.
.
Площадь
треугольника.
![]() ;
;
![]() ;
;
![]() (формула Герона).
Свойства
медиан, биссектрис, средних линий.
(формула Герона).
Свойства
медиан, биссектрис, средних линий.
а)
медианы
треугольника пересекаются в одной точке
и делятся этой точкой в отношении
![]() ,
считая от вершин;
,
считая от вершин;
б) три биссектрисы пересекаются в одной точке, являющейся центром вписанной окружности;
в)
биссектриса
делит противоположную сторону на части,
пропорциональные прилежащим к ней
сторонам:
![]() ;
г)
средняя линия параллельна третьей
стороне и равна ее половине.
Медиана треугольника
;
г)
средняя линия параллельна третьей
стороне и равна ее половине.
Медиана треугольника
![]() ,
проведенная к стороне
,
проведенная к стороне![]() ,
вы-
,
вы-
ражается через стороны треугольника по формуле
81
![]() .
.
Теорема
синусов:
![]() .
Теорема
косинусов:
.
Теорема
косинусов:
![]() .
.
Радиусы
вписанной и описанной окружностей
![]() ;
;
![]() .
.
Свойства равнобедренного треугольника
а) углы при основании треугольника равны;
б )
высота,
проведенная из вершины равнобедренного
треугольника, является также биссектрисой
и медианой.
Прямоугольный
треугольник
)
высота,
проведенная из вершины равнобедренного
треугольника, является также биссектрисой
и медианой.
Прямоугольный
треугольник
![]() (теорема Пифагора).
(теорема Пифагора).
![]() ,
,
![]() .
Признаки подобия треугольников
.
Признаки подобия треугольников
1) два угла одного треугольника равны двум углам другого;
2) две стороны одного треугольника пропорциональны двум сторонам другого и углы между этими сторонами равны;
3) три стороны одного треугольника пропорциональны трем сторонам другого.
 Свойства
подобных треугольников
У подобных треугольник отношение
периметров равно
Свойства
подобных треугольников
У подобных треугольник отношение
периметров равно
![]() ,
а
отношение площадей –
,
а
отношение площадей –
![]() (
–коэффициент
подобия).
II.
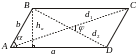
Четырехугольники
1)
Параллелограмм
(
–коэффициент
подобия).
II.
Четырехугольники
1)
Параллелограмм
![]() ,
,
![]() .
.
82
Свойства
параллелограмма:
а)
![]() ;
;
б) диагонали точкой пересечения делятся пополам;
в)
![]() .
Площадь
параллелограмма:
.
Площадь
параллелограмма:
![]()
2)
Ромб
– параллелограмм, все стороны которого
равны.
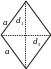 Свойства:
а)
Свойства:
а)
![]() ;
б) диагонали
ромба являются
биссектрисами его
внутренних углов.
;
б) диагонали
ромба являются
биссектрисами его
внутренних углов.
![]() .
3
.
3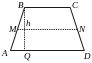 )
Трапеция.
Средняя линия трапеции параллельна
основаниям и равна их полусумме:
)
Трапеция.
Средняя линия трапеции параллельна
основаниям и равна их полусумме:
![]() .
Площадь:
.
Площадь:
![]() .
Если трапеция равнобедренная, т.е.
.
Если трапеция равнобедренная, т.е.
![]() ,
то углы при основании попарно равны:
,
то углы при основании попарно равны:
![]() .
.
I I.
Окружность и круг
I.
Окружность и круг
1)
Свойства
хорд окружности:
а)
диаметр, делящий хорду пополам
перпендикулярен этой хорде;
б)
равные хорды
равноудалены от центра окружности, и,
наоборот, равноудаленные от центра
окружности хорды равны;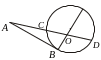
в)
между отрезками
пересекающихся хорд
![]() и
и
![]() имеет
место соотношение
имеет
место соотношение
83

![]() .
.
2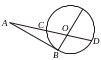 )
Касательная
и секущая
а)
)
Касательная
и секущая
а)
![]() б)
б)
![]() .
.
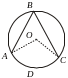
3)Углы
в окружности
а)
![]() –
вписанный угол;
–
вписанный угол;
![]() .
б)
.
б)
![]() – центральный угол.
– центральный угол.
![]() .
.
4)
Длины и площади в окружности и круге.
![]() – длина
окружности; (
– длина
окружности; (![]() –
радиус)
–
радиус)
![]() – длина дуги окружности с угловой
величиной в
– длина дуги окружности с угловой
величиной в
![]() ;
;
![]() – площадь круга;
– площадь круга;
![]() – площадь сектора с угловой величиной
дуги в
.
– площадь сектора с угловой величиной
дуги в
.
IV. Вписанные и описанные четырехугольники. 1) Для того, чтобы около четырехугольника можно было
описать
окружность, необходимо и достаточно,
чтобы
сумма противолежащих углов
этого четырехугольника бы-
ла равна
![]() .
Из всех параллелограммов лишь около
прямоугольника
(в частности,
квадрата) можно описать окружность.
Око-
ло трапеции можно описать
окружность тогда и только
.
Из всех параллелограммов лишь около
прямоугольника
(в частности,
квадрата) можно описать окружность.
Око-
ло трапеции можно описать
окружность тогда и только
84
тогда, когда она равнобедренная. 2) Для того, чтобы в четырехугольник можно было вписать
окружность необходимо и достаточно, чтобы суммы длин
противолежащих сторон этого четырехугольника были
 равны.
Из всех параллелограммов лишь в ромб
(в частности, в
квадрат) можно вписать
окружность.
равны.
Из всех параллелограммов лишь в ромб
(в частности, в
квадрат) можно вписать
окружность.
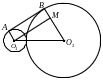
Пример 1. Радиус одной из двух касающихся внешним образом окружностей равен 1, а длина их общей касательной равна 4. Найти радиус второй окружности.
Решение.
Пусть
![]() –
общая
касательная;
–
общая
касательная;
![]() ;
и
;
и
![]() –
радиусы окружностей,
–
радиусы окружностей,
![]() .
( Если радиусы равны, то
.
( Если радиусы равны, то
![]() ).
Проведем
).
Проведем
![]() .
.
![]()
![]() .
Из прямоугольного треугольника
.
Из прямоугольного треугольника
![]() :
:
![]() ,
откуда
,
откуда
![]() ,
т.е.
,
т.е.
![]() .
Ответ:
.
Ответ:
![]() .
Пример
2. В окружность,
радиус которой равен
.
Пример
2. В окружность,
радиус которой равен
![]() ,
вписана трапеция; ее вершины делят
окруж-ность в отношении
,
вписана трапеция; ее вершины делят
окруж-ность в отношении
![]() .
Найти площадь трапеции.
.
Найти площадь трапеции.
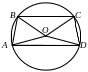 Решение.
Пусть
Решение.
Пусть
![]() .
Тогда:
.
Тогда:
![]() ;
;
![]() ;
;
![]() .
Центр
.
Центр
![]() окружности находится внутри трапеции.
окружности находится внутри трапеции.
![]()
85
![]()
![]()
![]()
Ответ:
![]() .
Пример 3.
В прямоугольной трапеции большая
диагональ, имеющая длину 24, является
биссектрисой острого угла. Найти площадь
трапеции, если расстояние от вершины
тупого угла до диагонали равно 9.
.
Пример 3.
В прямоугольной трапеции большая
диагональ, имеющая длину 24, является
биссектрисой острого угла. Найти площадь
трапеции, если расстояние от вершины
тупого угла до диагонали равно 9.
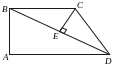 Решение.
Пусть
Решение.
Пусть
![]()
основание перпендикуляра, опущенного
из точки
основание перпендикуляра, опущенного
из точки
![]() на диагональ
на диагональ
![]() .
.
В
![]() :
:
![]()
(по
условию
![]() ,
а
,
а
![]() ).
Поэтому
).
Поэтому
![]() равно-
бедренный:
равно-
бедренный:
![]() .
Из
.
Из
![]() :
:
![]() .
.
Треугольники
![]() и
и
![]() подобны (по двум углам). Следовательно:
подобны (по двум углам). Следовательно:
![]() ,
т.е.
,
т.е.
![]() ,
откуда
,
откуда
![]() ;
;
![]() ,
т.е.
,
т.е.
![]() ,
откуда
,
откуда
![]() .
.
![]() .
.
Ответ:
![]() .
Пример 4.
В четырехугольнике
.
Пример 4.
В четырехугольнике
![]() ,
который вписан в окружность, стороны
,
который вписан в окружность, стороны
![]() и
и
![]() равны соответственно
равны соответственно
![]() и
и
![]() ,
угол
равен
,
угол
равен
![]() .
Найти площадь четырехугольника, если
известно, что его диагонали взаимно
перпендикулярны.
.
Найти площадь четырехугольника, если
известно, что его диагонали взаимно
перпендикулярны.
86
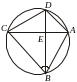 Решение.
Из треугольника
Решение.
Из треугольника
![]() по
теореме косинусов имеем:
по
теореме косинусов имеем:
![]()
![]() .
.
![]() .
.
Далее,
![]()
![]() .
.
С
другой стороны,
![]() .
.
Отсюда:
![]() .
По теореме Пифагора:
.
По теореме Пифагора:
![]() .
.![]() .
По
свойству пересекающихся хорд:
.
По
свойству пересекающихся хорд:
![]() ,
откуда
,
откуда
![]()
![]() .
.
Искомая площадь четырехугольника :
![]()
![]()
Ответ: Пример 5. Величины углов треугольника относятся как 2:3:7. Длина наименьшей стороны равна 5. Найти радиус ок- ружности, описанной около этого треугольника.
Решение.
Пусть в треугольнике![]() ,
–
радиус описанной окружности.
,
–
радиус описанной окружности.
87
Так
как
![]() ,
то
,
то
![]() ,
,
![]() ,
,
![]() .
Наименьшая сторона треугольника
лежит напротив наи-
меньшего угла,
т.е.
.
Наименьшая сторона треугольника
лежит напротив наи-
меньшего угла,
т.е.
![]() .
По теореме синусов имеем:
.
По теореме синусов имеем:
![]() ,
т.е.
,
т.е.
![]() .
.
 Ответ:
5.
Ответ:
5.
Пример 6. Из точки, лежащей вне круга, проведены две секущие, внешние части которых равны 2. Определить площадь четырехугольника, вершинами которого служат точки пересечения секущих с окружностью, зная, что длины двух его противоположных сторон равны 6 и 2,4 .
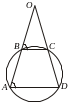 Решение.
По свойству
секущих:
Решение.
По свойству
секущих:
![]() .
Но
.
Но
![]() ,
следовательно,
,
следовательно,
![]() и
и
![]() .
Тогда
и
.
Тогда
и
![]() параллельны как прямые, отсекающие на
сторонах угла
параллельны как прямые, отсекающие на
сторонах угла
![]() равные отрезки, и
трапеция. Треугольники
равные отрезки, и
трапеция. Треугольники
![]() и
и
![]() подобны с коэффициентом
подобия
подобны с коэффициентом
подобия
![]() .
.
![]() ,
откуда
,
откуда
![]() .
.
![]() .
.
По
формуле Герона:
![]() .
.
Искомая
площадь:
![]()
Ответ:
![]() .
.
88
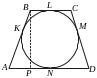 Пример
7. Равнобедренная
трапеция описана около круга. Боковая
сторона трапеции делится точкой касания
на отрезки
длиной 12 и 48. Найти площадь
трапеции.
Решение.
Пример
7. Равнобедренная
трапеция описана около круга. Боковая
сторона трапеции делится точкой касания
на отрезки
длиной 12 и 48. Найти площадь
трапеции.
Решение.
![]() –
точки касания окружности со сторонами
–
точки касания окружности со сторонами
![]() соответственно;
соответственно;
![]() .
Так как трапеция равнобедрен-
ная,
то
.
Так как трапеция равнобедрен-
ная,
то
![]() –
середина
–
середина
![]() ,
,
![]() –
се-
редина
–
се-
редина
![]() Тогда
Тогда
![]() ,
,
![]() .
Пусть
.
Пусть
![]() .
Тогда
.
Тогда
![]() .
Из
прямоугольного треугольника
.
Из
прямоугольного треугольника
![]() имеем:
имеем:
![]() .
.
![]() .
Ответ:
2880
.
Ответ:
2880
 Пример
8. В трапеции
Пример
8. В трапеции
![]() с основаниями
с основаниями
![]() и
биссектриса угла
и
биссектриса угла
![]() проходит через середину
проходит через середину
![]() стороны
стороны
![]() .
Известно, что
.
Известно, что
![]() .
Найти длину отрезка
.
Найти длину отрезка
![]() .
Решение.
Проведем
среднюю линию
.
Решение.
Проведем
среднюю линию
![]() .
.
![]() .
Поэтому,
треугольник
.
Поэтому,
треугольник
![]() равнобедренный:
равнобедренный:
![]() .
.
![]() .
Тогда
.
Тогда
![]() .
.
Пусть
![]() .
Из прямоугольного треугольника
.
Из прямоугольного треугольника
![]() :
:
![]() .
Из
треугольника
.
Из
треугольника
![]() по
теореме косинусов получим:
по
теореме косинусов получим:
89
![]() ;
;![]() .
.
Ответ: 3. ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ 1. Радиус окружности, вписанной в ромб, равен 6, периметр
ромба равен 96. Найти в градусах тупой угол ромба. (Ответ: 150)
2.
Точки
![]() и
и
![]() лежат на окружности. Найти в градусах
величину угла
лежат на окружности. Найти в градусах
величину угла
![]() ,
если точка
,
если точка
![]() и центр окружности
лежат по разные стороны от хорды
и центр окружности
лежат по разные стороны от хорды
![]() ,
а длина хорды
равна радиусу окружности.
(Ответ:
150)
,
а длина хорды
равна радиусу окружности.
(Ответ:
150)
3. Около круга радиуса 4 описан прямоугольный треугольник
с гипотенузой 26. Найти периметр этого треугольника. (Ответ: 60)
4. Разность длин оснований трапеции равна 14 , длины боко-
вых сторон равны 13 и 15. Вычислить площадь трапеции при условии, что в эту трапецию можно вписать окружность. (Ответ: 168)
5.
Из точки
![]() ,
находящейся на расстоянии 5 от центра
ок-
,
находящейся на расстоянии 5 от центра
ок-
ружности
радиуса 3 , проведены две секущие
![]() и
и
![]() ,
угол между которыми равен
,
угол между которыми равен
![]() (
(
![]() и
и
![]() –
точки пере-
–
точки пере-
сечения секущих с окружностью). Найти площадь треуголь-
ника
![]() ,
если площадь треугольника
равна 10.
(Ответ:
1,6)
,
если площадь треугольника
равна 10.
(Ответ:
1,6)
6.
Высоты треугольника равны 12 , 15 , 20.
Найти в градусах
больший угол
треугольника. (Ответ:
![]() )
7.
В окружность
радиуса 10 вписан равнобедренный тре-
)
7.
В окружность
радиуса 10 вписан равнобедренный тре-
угольник, у которого сумма длин основания и высоты равна
диаметру окружности. Найти высоту треугольника. (Ответ: 4)
90
8.
Окружность радиуса
![]() проходит через две смежные вер-
шины квадрата. Касательная к окружности,
проведенная из
третьей вершины
квадрата, вдвое больше стороны квадрата.
Найти площадь квадрата.
(Ответ:
4)
9. В
выпуклом равностороннем шестиугольнике
проходит через две смежные вер-
шины квадрата. Касательная к окружности,
проведенная из
третьей вершины
квадрата, вдвое больше стороны квадрата.
Найти площадь квадрата.
(Ответ:
4)
9. В
выпуклом равностороннем шестиугольнике
![]() углы при вершинах
углы при вершинах
![]() и
и
![]() – прямые. Найти площадь
шестиугольника,
если его сторона равна
– прямые. Найти площадь
шестиугольника,
если его сторона равна
![]() .
.
