Нерсисян 7

МИНОБРНАУКИ РОССИИ

Санкт-Петербургский государственный

электротехнический университет

«ЛЭТИ» им. В.И. Ульянова (Ленина)

Кафедра алгоритмической математики

отчет

по домашнему заданию №7

по дисциплине «Вычислительная математика»

Тема: Интерполяционный сплайн: Решение ленточной системы линейных уравнений методом прогонки

Вариант № 61

Студент гр. 8363		Нерсисян А.С.
Преподаватель		Коточигов А.М.

Санкт-Петербург

2020

Выполнение работы

Исходные данные:

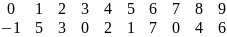
Построить периодический интерполяционный сплайн на отрезке

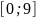
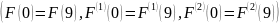найти коэффициенты ,

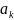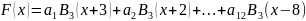проходящий через заданные точки

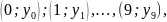
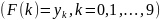
Решение:

1. Схема получения из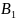 , описание 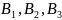(формулы на отрезках разбиения).

Составим с помощью формулы

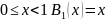
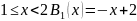
По рекуррентной формуле найдем 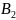и

Соответственно :

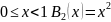
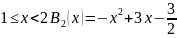
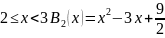
Соответственно :

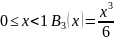
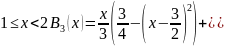
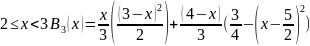
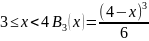
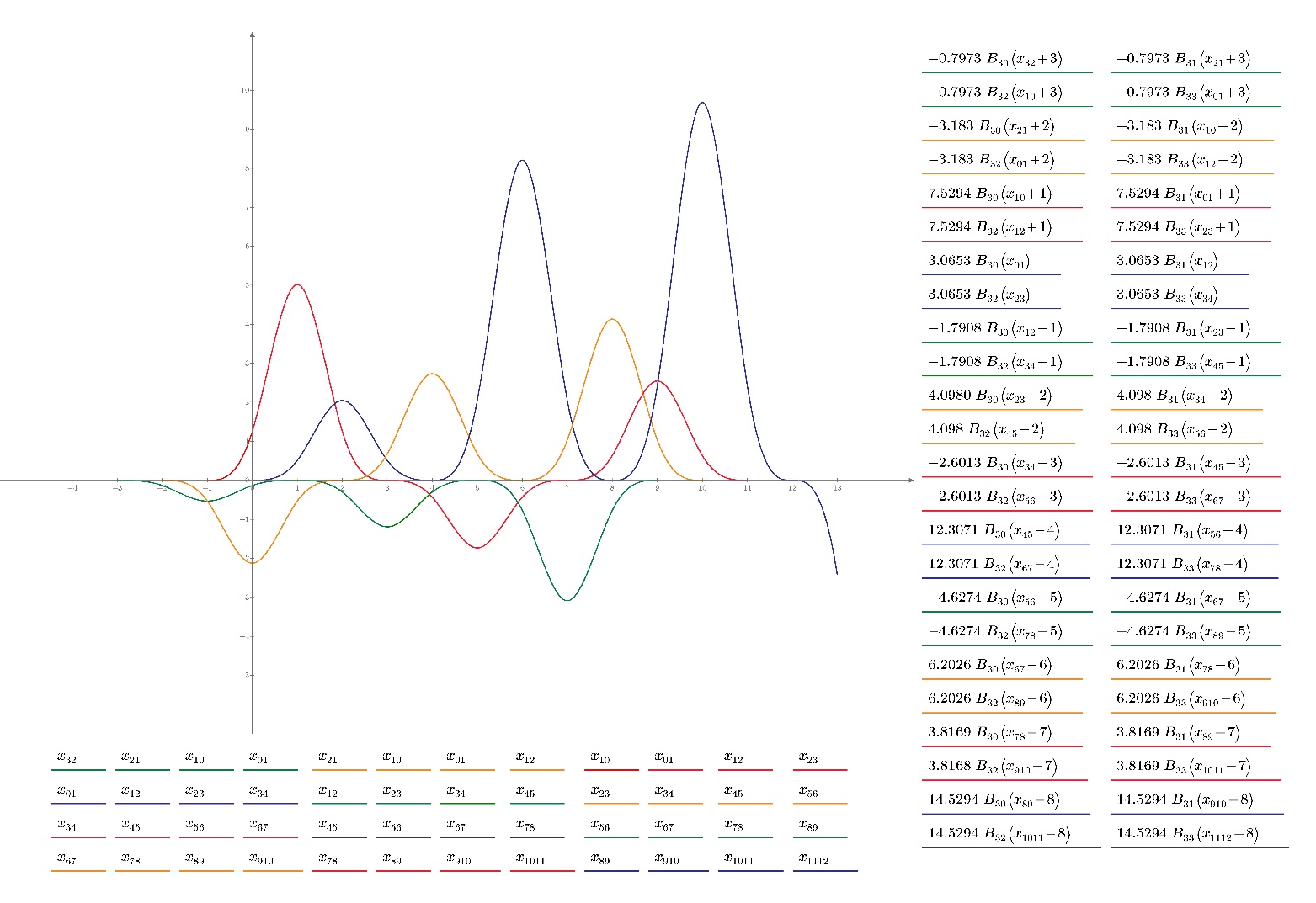
2. Рисунок с графиками (совместно)

Кубический сплайн определяет 3 точки, следовательно, чтобы определить 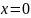нам потребуется сдвинуть сплайн на точку 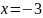. В точке 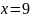кубический сплайн будет равен 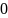, следовательно, потребуется сместить сплайн только до точки

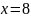
Чтобы определить все точки потребуется смещать кубический сплайн с 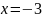до

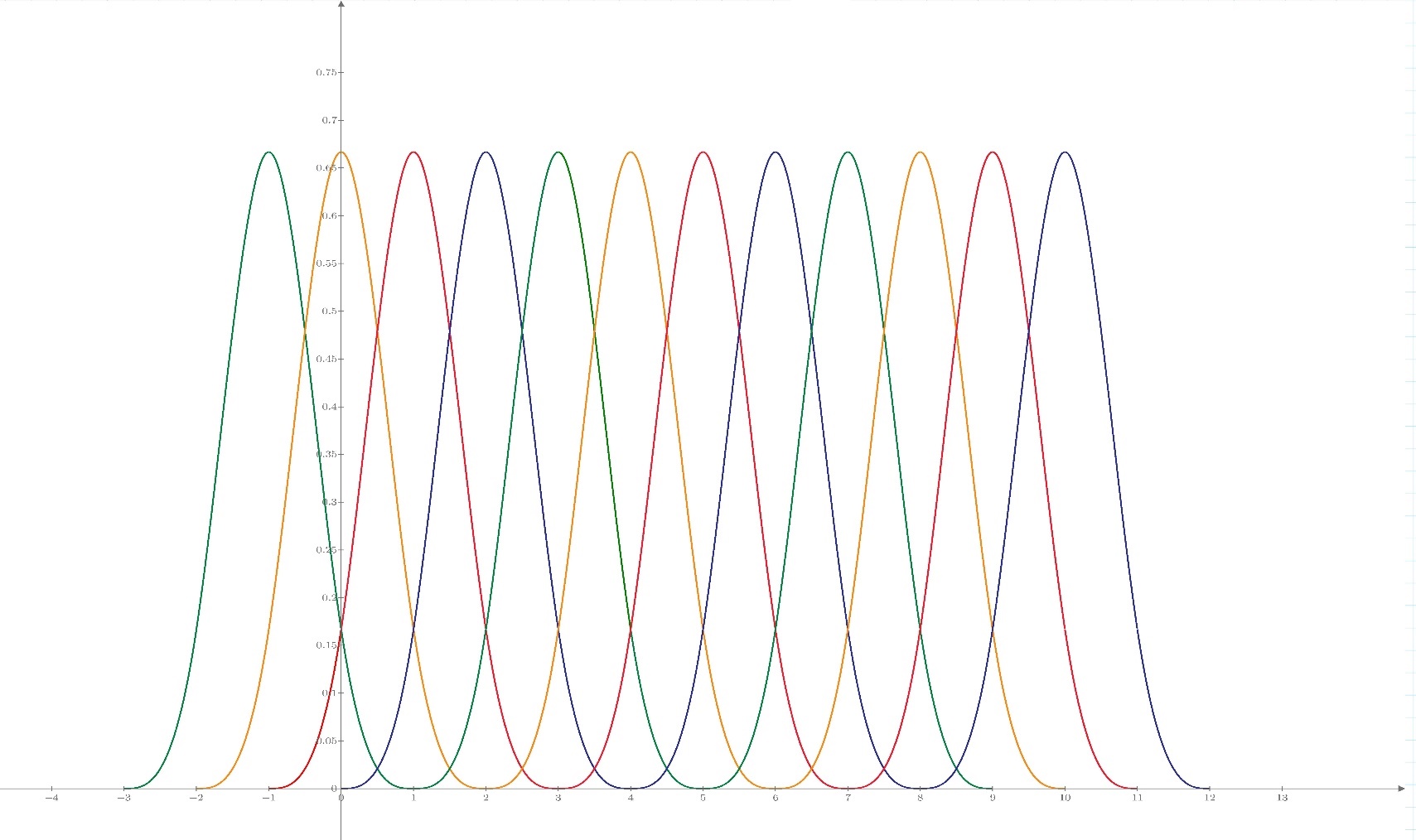( Рисунок графика (со всеми формулами) в более высоком разрешении был отправлен отдельно)

В итоге наша функция F примет вид

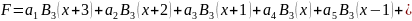
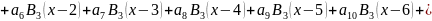
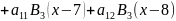
При подстановки у нас получится 10 уравнений, а неизвестных 12, следовательно получим два дополнительных уравнения с помощью первой и второй производной.

3. Распечатка матрицы коэффициентов для системы, определяющей неизвестные коэффициенты (10 уравнений, 12 неизвестных).

Матрица коэффициентов для системы уравнений, полученных с помощью сдвигов кубических сплайнов примет следующий вид ( ):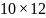

4. Два дополнительных уравнения отвечающих за периодичность

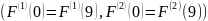
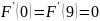и

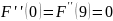
Уравнение от первой производной примет вид:

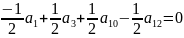
Уравнение от второй производной примет вид:

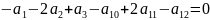
5. Расширенная матрица коэффициентов ( ).

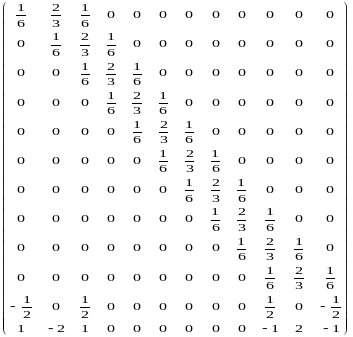
Матрица коэффициентов системы уравнений с подстановкой имеет вид ( ):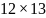

6. Записать основные этапы решения системы методом прогонки.

В матрице коэффициентов системы уравнений рассмотрим подматрицу и применим для нее метод прогонки:

С помощью элементарных преобразований уберем элементы в подматрице, находящиеся под главной диагональю (данные элементы помечены зеленым)

Проделаем несколько элементарных преобразований в матрице ( ), а именно:

1. Из второй строки отнимаем первую строку умноженную на

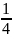
2. Из третей строки отнимаем вторую строку умноженную на

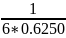
3. Из четвертой строки отнимаем третью строку умноженную на

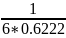
Таким образом уберем поддиагональные элементы в подматрице.

После преобразований матрица имеет следующий вид:

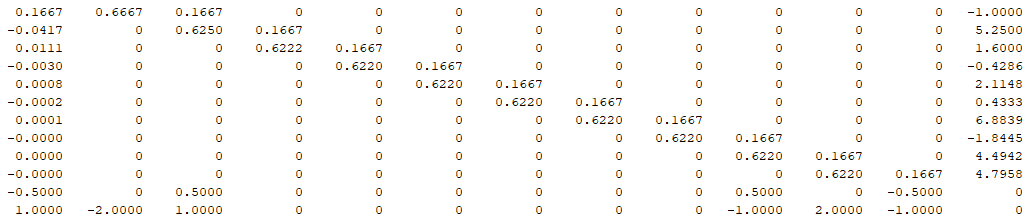
Преобразуем подматрицу так, чтобы по диагонали стояли единицы

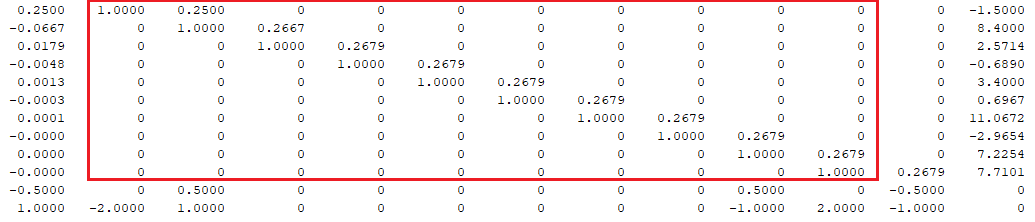
Далее уберем элементы над главной диагонали в подматрице, путем элементарных преобразований, а после, преобразуем подматрицу к виду единичной матрицы (делим строку на элемент в этой строке, стоящий в главной диагонали подматрицы)

С помощью преобразований поставим на место 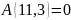. Для этого из одиннадцатой строки отнимаем вторую строку умноженную на

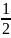
Далее поставим на место 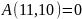. Для этого из одиннадцатой строки отнимаем девятую строку умноженную на

Тем же путем обнулим

Теперь выделим в ней подматрицу и решим ее, тем самым найдем 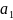и

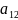
Составим систему и решим:

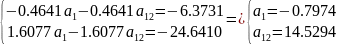
Далее постепенно подставляя вместо и их значения получим остальные коэффициенты:

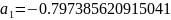
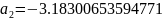
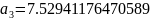
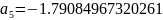
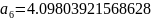
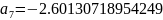
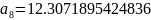
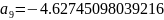
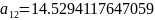
Подставим коэффициенты и “соберем” функцию F

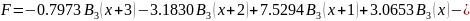
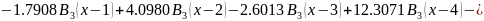
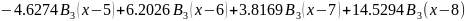
7. Нарисовать график 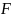(для получения графика нужно “склеить” его 12 составляющих).

(изображение в высоком разрешении отправлен отдельным файлом)