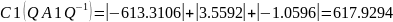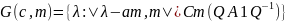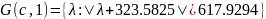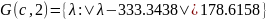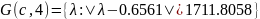Нерсисян_8363_5-исправл
.docxМИНОБРНАУКИ РОССИИ
Санкт-Петербургский государственный
электротехнический университет
«ЛЭТИ» им. В.И. Ульянова (Ленина)
Кафедра алгоритмической математики
13_4
пять (-)
в отчете должны быть определения
тогда моно сократить арифметику
и будет ясно причем тут оценки собственных чисел
отчет
по домашнему заданию №5
по дисциплине «Вычислительная математика»
Тема: «Оценка собственных чисел»
Вариант 61
Студент гр. 8363 |
|
Нерсисян А.С. |
Преподаватель |
|
Коточигов А.М. |
Санкт-Петербург
2020
Выполнение работы
Исходные данные:
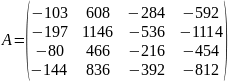
Решение:
Для заданной матрицы 𝐴
вычислить норму и найти вектор
реализующий норму
1)
если
Для заданной матрицы 𝐴 вычислим норму
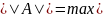
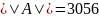
Найдём
вектор 𝑥
реализующий
норму
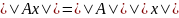
Так как |
берём
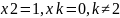тогда,
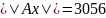
2) если ||𝑥|| = 𝑚𝑎𝑥(|𝑥_1|, . . . , |𝑥_4|)
Для заданной матрицы 𝐴 вычислим норму
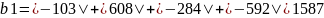
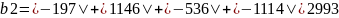
Найдём вектор 𝑥 реализующий норму
Так как
,
тогда
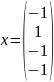
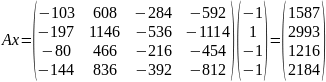
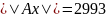
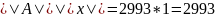
Подобрать матрицы 𝑃 и 𝑄, которые последовательно улучшают оценку для собственных чисел.
Для этого подберём одну из матриц элементарных преобразований. Составим матрицу, обнуляющий третий элемент первого столбца матрицы 𝐴.
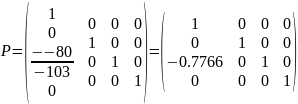
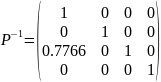
1)
Для заданной матрицы
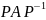вычислим
норму
||𝑃𝐴𝑃−1|| = 𝑚𝑎𝑥(|𝑎1|; |𝑎2|; |𝑎3|; |𝑎4|)
=
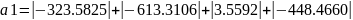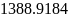
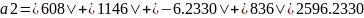
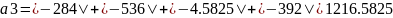
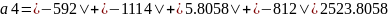
2) Для заданной матрицы вычислим норму
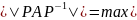
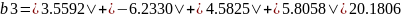
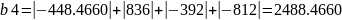
Для этого подберём одну из матриц
элементарных преобразований. Составим
матрицу, которая при последовательном
приведение матрицы к диагональному
виду обнуляет последний элемент второго
столбца матрицы
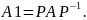
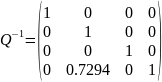
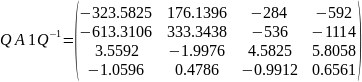
1)
Для заданной матрицы
вычислим
норму
=
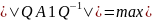
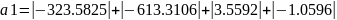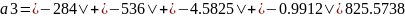
2) Для заданной матрицы вычислим норму
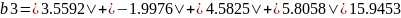
Проделаем аналогичную работу с кругами Гершгорина
Найдём строковые круги Гершгорина, для этого складываем абсолютные значения всех элементов строки, кроме этемента, находившаяся на главной диагонали.
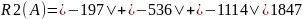
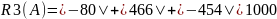
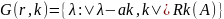
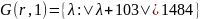
Найдём столбцовые круги Гершгорина, для этого складываем абсолютные значения всех элементов столбца, кроме этемента, находившаяся на главной диагонали.
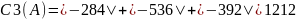
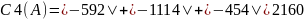
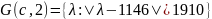
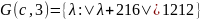
Для этого подберём одну из матриц элементарных преобразований. Составим матрицу, обнуляющий третий элемент первого столбца матрицы 𝐴.
Найдём строковые круги Гершгорина
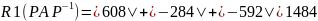
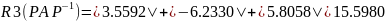
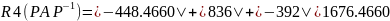
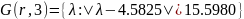
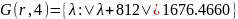
Найдём столбцовые круги Гершгорина
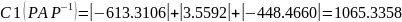
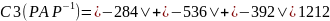
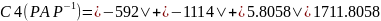
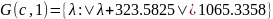
𝐺(𝑐, 4) = {λ: |λ + 812| <
}
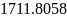Для этого подберём одну из матриц элементарных преобразований. Составим матрицу, которая при последовательном приведение матрицы к диагональному виду обнуляет последний элемент второго столбца матрицы
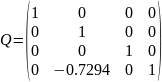
Найдём строковые круги Гершгорина
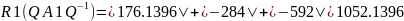
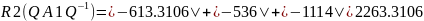
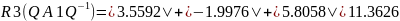
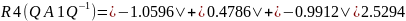
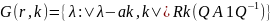
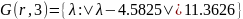
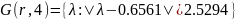
Найдём столбцовые круги Гершгорина
