ИДЗ -1

МИНОБРНАУКИ РОССИИ

Санкт-Петербургский государственный

электротехнический университет

«ЛЭТИ» им. В.И. Ульянова (Ленина)

Кафедра АМ

27_2, 7_3, 01_04_исправление

отчет

по домашнему заданию №1

по дисциплине «Вычислительная математика»

Тема: Линейные системы, число обусловленности

Вариант 11

Студентка гр. 8363		Нерсисян А.С.
Преподаватель		Коточигов А.М.

Санкт-Петербург

2020

Выполнение работы

Исходные данные:

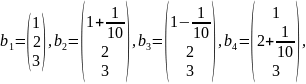
1. Описать элементарные преобразования 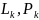, приводящие матрицу к верхнетреугольному виду. Записать разложение 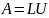, L – нижнетреугольная, U – верхнетреугольная.

Решение:

Преобразуем матрицу 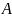к верхнетреугольному виду, используя

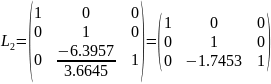
Привели матрицу к верхнетреугольному виду

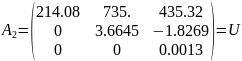
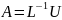
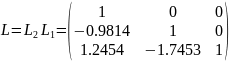
Обратная матрица к матрице

В итоге получим разложение матрицы

2. Описать элементарные преобразования , приводящие матрицу к диагональному виду. Написать решение систем

Рассмотрим 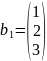и составим матрицу по методу Гаусса

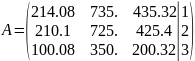
Чтобы поставить наибольший элемент на место , поменяем местми первый и второй столбцы,

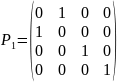
После преобразования матрица примет вид:

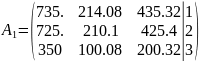
Далее преобразуем матрицу к верхнетреугольному виду, используя

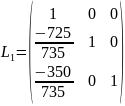
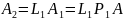
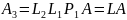
Привели матрицу к верхнетреугольному виду

Далее преобразуем матрицу к диагональному виду, для этого рассчитаем матрицы

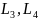
Привели матрицу к диагональному виду det=0 (исправил, проблемы были с оформлением, все расчеты были верны)

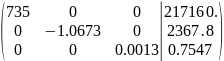
Собственный вектор

Для

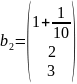
Для

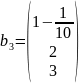
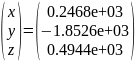
Для

Для

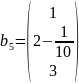
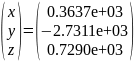
Для

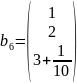
Для

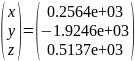
3. Вычислить сингулярные числа матрицы , найти число обусловленности матрицы в норме

Так как матрица не симметричная сначала найдём

(исправленно описание а также оформление)

Найдём собственные числа матрицы через характеристическое уравнение (по определению определителя)

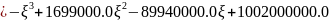
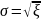
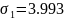
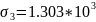
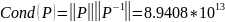
Сравним сингулярные числа и собственные числа матрицы.

Найдём собственные числа матрицы через характеристическое уравнение (по определению определителя)

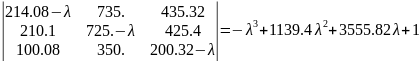
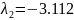
4. Прокомментировать соотношение решений систем для

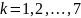
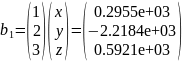
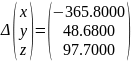
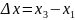
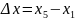
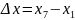
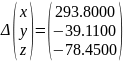
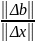
	0.1649	0.0267	1.6191
	0.1649	0.0267	1.6191
	0.2311	0.0267	1.5553
	0.2311	0.0267	1.5553
	0.1324	0.0267	2.0166
	0.1324	0.0267	2.0166

При одинаковом для всех Δ𝑏 не будет одинаковым

5. Найти числа обусловленности матриц в норме

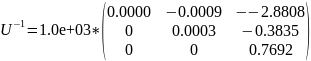
(исправленно описание)

Найдем числа обусловленности для матриц и . Для этого посчитаем нормы этих матриц ( и ), и нормы матриц обратные к и

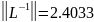
Число обусловленности матрицы, по определению это перемножение норм матрицы и матрицы ее обратной.