Нерсисян_8363_2_(исправление)

МИНОБРНАУКИ РОССИИ

Санкт-Петербургский государственный

электротехнический университет

«ЛЭТИ» им. В.И. Ульянова (Ленина)

Кафедра алгоритмической математики

25.03.2020

отчет

по домашнему заданию №2

по дисциплине «Вычислительная математика»

Тема: Псевдорешение: Расстояние от точки до сдвига линейного подпространства

Вариант 11

Студент гр. 8363		Нерсисян А.С.
Преподаватель		Коточигов А.М.

Санкт-Петербург

2020

Выполнение работы

Исходные данные:

1. Для заданной матрицы А найти псевдообратную .

Решение:

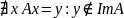
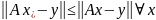
Для любой матрицы А существует единственный псевдообратный оператор

При этом для любого

либо

либо 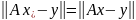при

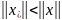
Найдем ранг матрицы А

Составим матрицу , состоящую из 4 столбцов матрицы А, так как ранг матрицы А равен 4.

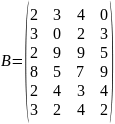
Найдем матрицу C. Для этого запишем все столбцы как линейные комбинации первых r столбцов

Первые r столбцов образуют единичную матрицу, значит матрица имеет ранг r.

Для построения псевдообратных матриц для B, C убедимся, что матрицы , обратимы. Это следует из того, что ранг матриц равны r, следовательно произведение , имеет размерность и ранг будет равен r.

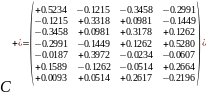
Получим псевдообратную матрицу

Проверим второе свойство для псевдообратной матрицы

Сделаем проверку по формуле

2. Подобрать вектор такой, что система имеет решение

3. Проверить, что вектор является решением системы

Решение:

Рассмотрим Для него

Мы подобрали вектор такой, что система имеет решение

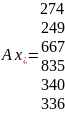
Вывод: вектор является решением системы

4. Найдем все псевдорешения где e- стандартный базис в

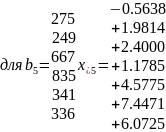
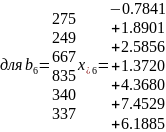
Найдем для каждого