empiv

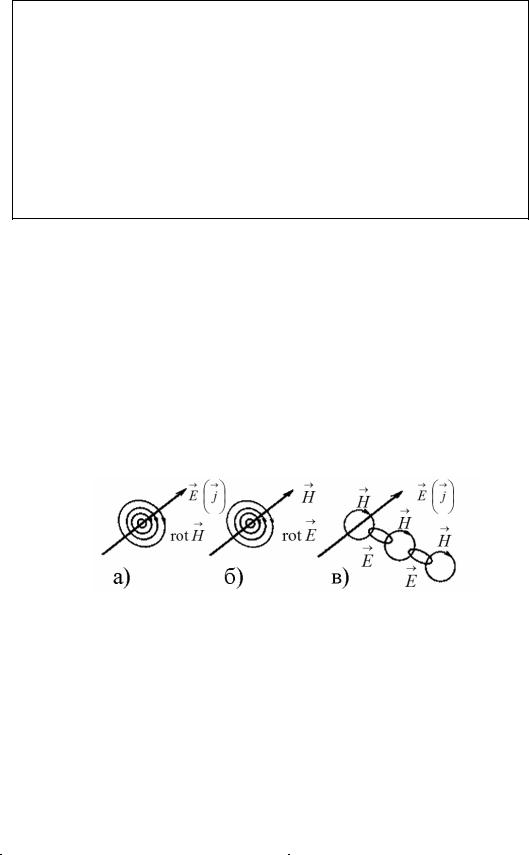
Закон сохранения заряда:

Уравнение непрерывности:

→

div j полн = 0

Закон Ома:

→→

j = σ E

Уравнения Максвелла в интегральной форме описывают электромагнитное поле в некоторых объёмах, ограниченных контурами и поверхностями интегрирования, а уравнения Максвелла в дифференциальной форме характеризуют поле в точках. Из уравнений следует, что электрическое и магнитное поля взаимосвязаны между собой и способны порождать друг друга. В частности, электрическое поле создает вокруг себя магнитное поле (рис.2.а), а всякое изменение магнитного поля сопровождается образованием электрического поля (рис.2.б). В целом изменение одного поля вызывает появление другого поля, в результате действует и существует суммарное электромагнитное поле (рис.2.в), переносящее энергию в атмосфере, кабелях, волноводах, световодах и любых других направляющих системах.

Рис.2 – Взаимосвязь векторов электромагнитного поля Однако, в ряде случаев взаимной обусловленностью электрического и магнитного по-

лей можно пренебречь. В соответствии с данным критерием среди всего многообразия электромагнитных полей принято выделять ряд классов:

- статические поля – поля, создаваемые системами неподвижных зарядов, постоянных магнитов и постоянных токов в тех областях, где токи отсутствуют; в этом случае система уравнений Максвелла распадается на две подсистемы, каждая из которых содержит либо электрические, либо магнитные величины:

- стационарное электромагнитное поле – поле, создаваемое системами неподвижных зарядов, постоянных магнитов и постоянных токов в тех областях, где токи существуют; от-

11

личие стационарного случая от статического состоит в том, что в анализируемой области пространства присутствуют постоянные токи; электрическое и магнитное поля можно счи-

- квазистационарное электромагнитное поле – поле, источники которого представ-

ляют собой относительно медленно меняющиеся во времени функции, таким образом, что пространственный период изменения поля оказывается существенно меньше, чем линейные размеры анализируемой области пространства. При этом описание электромагнитных явлений может быть осуществлено аналогично стационарному случаю;

- быстропеременные поля, для которых пространственный период изменения поля одного порядка или меньше размеров анализируемой области пространства; в этом случае целесообразно применение полной системы уравнений Максвелла

Особое место традиционно отводится монохроматическому электромагнитному полю,

как практически важному случаю. На самом деле, практически любой сигнал, встречающийся в радиотехнике может быть представлен в виде суперпозиции монохроматических составляющих. Монохроматическими называются процессы, изменяющиеся во времени по закону косинуса или синуса, описываемые соответственно скалярными и векторными функциями ви-

При анализе таких процессов широко используется метод комплексных амплитуд,

•

состоящий в формальной замене функции ψ на комплексное изображениеψ , следующим об-

•

что ψ = Reψ . Комплексное представление векторных величин выглядит следующим обра-

12

Поскольку уравнения Максвелла содержат только линейные операции, в случаях, в которых параметры среды не зависят от поля, формальная замена соответствующих величин их комплексными изображениями не меняет вида этих уравнений (все линейные операции могут проводиться раздельно над действительной и мнимыми частями комплексных величин).

Уравнения Максвелла для монохроматического поля выглядят следующим образом.

Первое уравнение Максвелла:

ность процессов имеющих место в веществе, связанных с воздействием электрического поля. Аналогичным образом записывается второе уравнение Максвелла для монохромати-

ческого поля:

Взятие операции дивергенции от обеих частей (23) и (25) позволяет легко показать, что третье и четвертое уравнения для монохроматического поля выводятся соответственно из первого и второго.

При записи уравнений Максвелла под вектором плотности тока проводимости подразумевается плотность тока, который возникает в проводящей среде под воздействием электрического поля. Однако, помимо это-

му же, они считаются известными. Эти токи принято называть сторонними.

вводятся сторонние заряды.

С учетом сторонних источников уравнения Максвелла в имеют вид:

13

4.Граничные условия и краевые задачи электродинамики

Вэлектродинамике встречается ряд задач по вычислению поля вблизи границы раздела сред с макроскопическими параметрами. При этом возникает следующая ситуация: макроскопические параметры среды изменяются в пределах объема диффузии сред. Как правило, линейные размеры этого объема оказываются сравнимы с внутримолекулярными размерами вещества, что позволяет предполагать, с макроскопической точки зрения, что параметры ε, µ, σ меняются скачкообразно. При скачкообразном изменении одного или нескольких параметров разрыв будут претерпевать функции, стоящие под знаком производной в уравнениях Максвелла, поэтому эти уравнения в дифференциальной форме утрачивают свой физический смысл. Для компенсации разрывов векторов поля при

Далее из уравнений Максвелла получают систему граничных условий, раздельно формулируемых для тангенциальных и нормальных составляющих векторов поля:

Полная система граничных условий

D1n − D2 n = ρ S ;

E1τ = E2τ ;

(26)

B1n = B2 n ;

H1τ − H 2τ = jS .

Если одна из сред может считаться идеальным проводником, поле во второй среде от-

→→ → →

сутствует, D 2 = E 2 = B 2 = H 2 = 0 и система граничных условий принимает вид:

14

ческую задачу – значит отыскать такие функции (либо векторы поля, либо заряды и токи), которые удовлетворяют уравнениям Максвелла и граничным условиям.

Электродинамические задачи, как и любые задачи математической физики, традиционно задачи подразделяют на прямые и обратные. Сторонними источниками в прямых задачах являются заряды и токи, в обратных – векторы поля. Как правило, исследование реальных физических процессов требует многократного поочередного решения прямых и обратных задач. Кроме того, задачи электродинамики разделяют на внутренние и внешние. Внутренняя задача сводится к вычислению поля внутри некоторой области, ограниченной замкнутой идеально проводящей поверхностью. Решение внешней задачи определяется полем в области внешней по отношению к поверхности, на которой распределены сторонние источники.

5. Энергетические соотношения в электродинамике

Поскольку электромагнитное поле материально, то для него выполняется закон со-

хранения и превращения энергии.

Пусть V – произвольный объем (рис.4), в котором существует электромагнитное поле. В объеме определенным образом распределены сторонние источники с суммарной мощно-

→

стью Рст. Умножим каждый член первого уравнения Максвелла скалярно на E , а каждый

→

член второго уравнения Максвелла скалярно на H и вычтем второе получившееся уравне-

15

Все слагаемые правой части имеют смысл соответствующих объемных плотностей мощностей, в левой части – плотность мощности сторонних источников. Кроме того, произ-

скорость изменения во времени объемной плотности энергии электромагнитного поля в объеме V. Каждый член, стоящий под знаком производной, представляет собой соответственно объемные плотности энергии электрического и магнитного полей. Таким образом, со временем энергия электрического поля переходит в энергию магнитного поля и наоборот.

Полученное уравнение носит название теоремы Умова-Пойтинга в интегральной форме. Анализ (29) позволяет заключить, что энергия электромагнитного поля может быть вычислена по формуле:

V

→

Вектор П имеет смысл плотности потока энергии, то есть определяет электромагнитную энергию, переносимую через единицу поверхности в единицу времени и носит название вектора Пойнтинга. Таким образом, теорема Умова-Пойтинга является формулировкой закона сохранения и превращения энергии для электромагнитного поля.

Рассмотрим далее формулировку закона сохранения энергии для монохроматического электромагнитного поля, поскольку она содержит ряд специфических особенностей.

При рассмотрении периодических процессов удобно анализировать не мгновенные

T

значения, а их средние за период значения определяемые как f ср = 1 ∫ f (t)dt .

T 0

Воспользуемся следующими преобразованиями, не имеющими четкого физического смысла, однако позволяющими избежать изменения вида уравнений, проявляющегося при выполнении нелинейных операций по вычислении энергетических характеристик:

16

Тогда вектор Пойнтинга может быть выражен как:

тор Пойнтинга. Средняя за период мощность тепловых потерь определяется выражением:

2 V

Средняя мощность сторонних источников записывается как:

V

Средние за период энергии электрического и магнитного полей:

V

Проводя преобразования, аналогичные использованным при выводе (29) нетрудно по-

казать, что теорема Умова-Пойнтинга для монохроматического поля будет иметь вид:

Нижеследующая запись позволяет выявить физический смысл входящих в (34) слагаемых:

S

Выделяя в (35) действительную и мнимую части легко получить, соответственно,

уравнения баланса активных и реактивных мощностей:

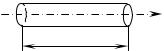
Определим далее скорость распространения электромагнитной энергии, для чего выделим в объеме, в котором существует электромагнитное поле, цилиндр с площадью основания S и длиной l (рис.4).

17

6. Электромагнитное поле волнового характера (поле излучения)

Система дифференциальных уравнений Максвелла представляет собой систему из 4-х векторных уравнений (12 скалярных, если задача 3-х мерная), причем в первые два из них входит электрическая и магнитная величины. С практической точки зрения представляет интерес уменьшение размерности системы уравнений.

Исторически сложилось так, что ЭМП в однородной изотропной среде принято характеризовать двумя векторными функциями (силовыми характеристиками), хотя такой способ описания не является единственным. Следовательно, для представления целесообразно выбрать иную систему векторных или скалярных функций, так, чтобы уравнения описывались наиболее простым способом. Такими функциями являются разного рода электродина-

мические потенциалы.

Рассмотрим произвольный объем V, в котором определенным образом дислоцирова-

→

ны проводящие тела и сторонние источники электрического типа j ст , где

→

r − радиус-вектор точки наблюдения,

→

r ′− радиус-вектор точки поверхности, несущей сторонний ток.

Исключая в уравнениях Максвелла электрический или магнитный вектор и вводя векторный и скалярный электродинамические потенциалы для сокращения размерности системы следующим образом

нетрудно получить уравнение второго порядка относительно векторного потенциала:

→

При этом на А и ϕ накладывается условие Лоренцевой калибровки:

18

V

Аналогичные рассуждения приводят к решению для скалярного потенциала:

→

где ρ( r ′ ) − поверхностный заряд, наведенный на поверхности проводника, связанный с плотностью поверхностного тока законом сохранения электрического заряда:

→→

Наличие множителя r − r′ в экспоненте в функции Грина указывает на то обстоя-

тельство, что интегралы (41-42) описывают волновой процесс, а источники в условиях настоящей задачи, являются источниками излучения.

Излучением называется процесс создания в пространстве электромагнитного поля волнового характера. Волновое поле описывается запаздывающими функциями и представляет собой процесс, переносящий энергию.

Следовательно, не всякое поле является полем излучения, т.к. не переносит энергию (например, статическое поле). С точки зрения теории Максвелла уход энергии в виде электромагнитного поля так же естественен, как ответвление электрической энергии по ветвям электрической цепи.

По характеру электромагнитного поля, излучаемого источником возмущения во внешнее пространство, это пространство делится на две зоны: ближнюю и дальнюю. Ближ- ней зоной называется ближайшая к источнику возмущения область пространства, для кото-

19

рой длина волны существенно больше расстояния. Дальняя зона - это область пространства,

вкоторой расстояние от источника существенно превышает длину волны. Границей раздела этих зон условно можно принять равенство расстояния от источника возмущения 1/6 длины волны. Электромагнитное поле, действующее в ближней зоне, называется полем индукции, а

вдальней — полем излучения.

Вближней зоне электрическое и магнитное поля сдвинуты по фазе на 90°, а вектор Пойнтинга имеет лишь реактивную составляющую, поэтому вся энергия электромагнитного поля сосредоточена около источника возмущения и непрерывный перенос энергии во внешнее пространство, характерный для процессов излучения, отсутствует. В ближней зоне происходят преимущественно местные перемещения энергии, связанные с периодическими преобразованиями электрической энергии в магнитную, и обратно. В дальней зоне имеет место процесс излучения электромагнитной энергии: часть энергии от источника возмущения переносится во внешнее пространство на большее расстояние от источника.

Не всякое поле является полем излучения, т.к. не переносит энергию (например, статическое поле). С точки зрения теории Максвелла уход энергии в виде электромагнитного поля так же естественен. как ответвление электрической энергии по ветвям электрической цепи.

Элементарный электрический вибратор (излучатель) – ЭЭВ.

ЭЭВ называется электрически малый отрезок прямолинейного электрического (переменного) тока, амплитуда и фаза тока в каждой точ-

перейти от объемного интервала к интервалу по координате:

20