Метод парабол (метод Симпсона)

Использование трех точек для интерполирования подынтегрального выражения позволяет использовать параболическую функцию (полином второй степени). Это приводит к формуле Симпсона приближенного вычисления интеграла.

Рассмотрим произвольный интеграл

Воспользуемся заменой переменной таким образом, чтобы границы отрезка интегрирования вместо [a,b] стали [-1,1], для этого введем переменную z:

, тогда и

Рассмотрим задачу интерполирования полиномом второй степени (параболой) подынтегральной функции, используя в качестве узлов три равноудаленные узловые точки – z = -1, z = 0, z = +1 (шаг равен 1, длина отрезка интегрирования равна 2). Обозначим соответствующие значения подынтегральной функции в узлах интерполяции

Система уравнений для нахождения коэффициентов полинома

, проходящего через три точки , и

примет вид

или

Коэффициенты легко могут быть получены

Вычислим теперь значение интеграла от интерполяционного многочлена

Путем обратной замены переменной вернемся к исходному интегралу. Учтем, что

• соответствует

• соответствует

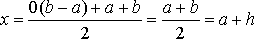
• соответствует

Получим формулу Симпсона для произвольного интервала интегрирования:

, и

При необходимости, исходный отрезок интегрирования может быть разбит на N сдвоенных отрезков, к каждому из которых применяется формула Симпсона. Шаг интерполирования при этом составит

Для первого отрезка интегрирования узлами интерполирования будут являться точки a, a+h, a+2h, для второго – a+2h, a+3h, a+4h, третьего a+4h, a+5h, a+6h и т.д. Приближенное значение интеграла получается суммированием N площадей:

В данную сумму входят одинаковые слагаемые (для внутренних узлов с четным значением индекса - 2i). Поэтому можно перегруппировать слагаемые в этой сумме таким образом

, что эквивалентно

, так как

Погрешность этого приближенного метода уменьшается пропорционально длине шага интегрирования в четвертой степени, т.е. при увеличении числа интервалов вдвое ошибка уменьшается в 16 раз

δ ~ h ⁴

Увеличение точности

Здесь мы рассмотрим так называемый процесс Эйткена. Он дает возможность оценить погрешность метода и указывает алгоритм уточнения результатов. Расчет проводится последовательно три раза при различных шагах разбиения h₁, h₂, h₃, причем их отношения постоянны: h₂/ h₁= h₃/ h₂= q (например, при делении шага пополам q=0.5). Пусть в результате численного интегрирования получены значения интеграла I₁, I₂, I₃. Тогда уточненное значение интеграла вычисляется по формуле

а порядок точности используемого метода численного интегрирования определяется соотношением

.

Уточнение значения интеграла можно также проводить методом Рунге-Ромберга.

Из анализа погрешностей методов численного интегрирования следует, что точность получаемых результатов зависит как от характера изменения подынтегральной функции, так и от шага интегрирования. Будем считать, что величину шага мы задаем. При этом ясно, что для достижения сравнимой точности при интегрировании слабо меняющейся функции шаг можно выбирать большим, чем при интегрировании резко меняющихся функций.

На практике нередко встречаются случаи, когда подынтегральная функция меняется по-разному на отдельных участках отрезка интегрирования. Это обстоятельство требует такой организации экономичных численных алгоритмов, при которой они автоматически приспосабливались бы к характеру изменения функции. Такие алгоритмы называются адаптивными (приспосабливающимися). Они позволяют вводить разные значения шага интегрирования на отдельных участках отрезка интегрирования. Это дает возможность уменьшить машинное время без потери точности результатов расчета. Подчеркнем, что этот подход используется обычно при задании подынтегральной функции y=f(x) в виде формулы, а не в табличном виде.

Рассмотрим принцип работы адаптивного алгоритма. Первоначально отрезок [a,b] разбиваем на n частей. В дальнейшем каждый такой элементарный отрезок делим последовательно пополам. Окончательное число шагов, их расположение и размеры зависят от подынтегральной функции и допустимой погрешности e .

К каждому элементарному отрезку [x_i-1, x_i] применяем формулы численного интегрирования при двух различных его разбиениях. Получаем приближения для интеграла по этому отрезку:

Полученные значения сравниваем и проводим оценку их погрешности. Если погрешность находится в допустимых границах, то одно из этих приближений принимается за значение интеграла по этому элементарному отрезку. В противном случае происходит дальнейшее деление отрезка и вычисление новых приближений. С целью экономии времени точки деления располагаются таким образом, чтобы использовались вычисленные значения в точках предыдущего разбиения.

Процесс деления отрезка пополам и вычисления уточненных значений продолжается до тех пор, пока их разность станет не больше некоторой заданной величины d_i,зависящей от e и h:

.

Аналогичная процедура проводится для всех n элементарных отрезков. Величина принимается в качестве искомого значения интеграла. Условия и соответствующий выбор величин d_iобеспечивают выполнение условия