Задание 2. Определение реакций опор твердого тела

Конструкция состоит из двух взаимно перпендикулярных тонких однородных прямоугольных пластин веса P₁ иP₂ , жестко соединенных друг с другом. ВершинаAпервой пластиныABCD расположена в начале неподвижной прямоугольной системы координат. Бóльшая сторона второй пластины совпадает с одной из сторон первой пластины. Координаты вершинB иCпервой пластины, совпадающие стороны пластин и координаты вершиныG второй пластины указаны в табл. 3. ВершиныDпервой пластины иHвторой пластины определяются построением. Конструкция удерживается в положении равновесия сферическим шарниромA, цилиндрическим шарниромB(направление оси шарнира совпадает с направлением оси, на которой расположена точкаB) и тонким невесомым стержнемDE, прикрепленным к пластинеABCDи к одной из координатных осей в точкеEсферическими шарнирами.

Конструкция загружена парой сил с алгебраическим моментом M, плоскость действия которой совпадает с плоскостью одной из пластин, и силой , приложенной к точкеC, образующей с положительными направлениями координатных осей углыи. Плоскость действия пары сил, значенияM, P₁ , P₂ , F, иуказаны в табл. 4. Единицы задаваемых величин:M– килоньютон-метр (кНм);P₁ , P₂ , F– килоньютон (кН). Углыипредставлены в градусах, а координаты точек – в метрах.

Найдите реакции шарниров AиB, а также усилие в стержнеDE.

Указания к выполнению задания

Вначале необходимо изобразить три взаимно перпендикулярные оси x, yи z. Затем по координатам в соответствии с номером своего варианта задания надо построить вершиныA, BиСпрямоугольной пластиныABCD. Ее четвертая вершинаDбудет находиться на пересечении перпендикуляров, проведенных в точкахВ и С, к направлениям соответственноАВ и АС.Аналогично строится и вторая пластина. Далее в точкеАнеобходимо нарисовать сферический, а в точкеВ– цилиндрический шарниры. Ось цилиндрического шарнира должна быть направлена вдоль той координатной оси, на которой лежит эта точка. Тонкий невесомый стерженьDEкрепится в точкеDпластины и в точкеЕнеподвижного пространстваAxyzсферическими шарнирами. Для решения задачи на рисунке надо изобразить силы тяжести пластин, задаваемую силу , углы, которые образует этот вектор с положительными направлениями координатных осей, реакцию стержняDE, составляющие реакций шарнировА иВ и пару сил с алгебраическим моментомМ.После этого можно приступить к составлению шести уравнений равновесия пространственной системы сил. Как правило, составление первой тройки уравнений у студентов затруднений не вызывает.

Приступая к составлению второй тройки уравнений, необходимо помнить:

• для того чтобы найти момент силы относительно какой-либо оси, ее надо спроецировать на плоскость, перпендикулярную этой оси и найти алгебраический момент построенной проекции относительно точки пересечения оси с плоскостью;

• момент силы относительно оси равен нулю, если линия действия силы пересекает эту ось или ей параллельна.

Пример

Дано: B (0;0,85;0),C (0,4;0,85;0),G(0,4;0;-0,2),E(0;0;0,35),CD– совпадающие стороны пластин, 1-я пластина – плоскость действия пары,

кНм;кН;кН;кН;;;.

Определить реакции шарниров AиB, усилие в стержнеDE.

Решение. В точке пересечения диагоналей пластин приложими– силы тяжести пластин, а в плоскости первой пластины – пару сил с алгебраическим моментомM(рис. 8). К вершинеСпластиныABCDприложим силу, образующую углы,ис осями координатx,y иz.

Заменим действие шарниров АиВреакциями, а на рис. 8 изобразим их составляющие. Предполагая стерженьDEрастянутым, заменим его действие на пластину силой натяжения, направленной вдоль отсеченного стержня. Векторобразует со сторонойDAпластины угол φ, который нетрудно найти из треугольникаADE:

Таблица 3

Варианты задания 2

Вари-ант	Точка B			Точка C			Совпадающие стороны пластин	Точка G			Точка E
	xB	yB	zB	xC	yC	zC		xG	yG	zG	xE	yE	zE
1	0	0,8	0	0,4	0,8	0	CD	0,4	0	-0,2	0	0	0,6
2	0	0,5	0	0	0,5	1,0	AB	0,2	0	0	0,8	0	0
3	0,4	0	0	0,4	0	0,8	AB	0	0,2	0	0	1,0	0
4	0,5	0	0	0,5	0,8	0	CD	0	0,8	0,3	0	0	-0,8
5	0	0	0,6	0	1,2	0,6	CD	0,4	1,2	0	-0,3	0	0
6	1,0	0	0	1,0	0	0,5	AB	0	-0,3	0	0	0,8	0
7	0,5	0	0	0,5	1,2	0	AD	0	0	0,3	0	0	-0,7
8	0	0,6	0	0	0,6	1,0	CD	0,4	0	1,0	-0,3	0,0	0
9	0	0	0,6	1,0	0	0,6	BC	0	0,3	0,6	0	0,5	0
10	0,5	0	0	0,5	0,9	0	CD	0	0,9	-0,3	0	0	0,5
11	0	0	0,6	0	1,2	0,6	AB	0,3	0	0	1,0	0	0
12	0	0	0,9	0,6	0	0,9	CD	0,6	0,4	0	0	-1,1	0
13	0,5	0	0	0,5	1,1	0	AB	0	0	0,3	0	0	0,9
14	0	0,4	0	0	0,4	0,9	AB	-0,3	0	0	1,0	0	0
15	1,1	0	0	1,1	0	0,6	BC	1,1	-0,4	0	0	0,8	0
16	0	0,7	0	1,0	0,7	0	AB	0	0	0,5	0	0	1,0
17	0	1,0	0	0	1,0	0,6	BC	-0,3	1,0	0	1,2	0	0
18	0,7	0	0	0,7	0	1,1	AD	0	0,2	0	0	-0,8	0
19	0	0,5	0	1,0	0,5	0	AD	0	0	0,3	0	0	-1,2
20	0	0	0,9	0	0,5	0,9	BC	-0,4	0	0,9	1,1	0	0
21	1,2	0	0	1,2	0	0,7	AD	0	-0,4	0	0	1,0	0
22	0	0,6	0	0,8	0,6	0	CD	0,8	0	0,4	0	0	-1,0
23	0	1,0	0	0	1,0	0,8	AD	-0,4	0	0	0,9	0	0
24	0,5	0	0	0,5	0	1,0	CD	0	-0,3	1,0	0	0,4	0
25	0	0,6	0	1,2	0,6	0	BC	0	0,6	0,4	0	0	0,9
26	0	0	1,2	0	0,4	1,2	CD	-0,3	0,4	0	1,0	0	0
27	0	0	1,1	0,6	0	1,1	AD	0	0,4	0	0	-1,0	0
28	1,0	0	0	1,0	0,6	0	BC	1,0	0	-0,4	0	0	0,5
29	0	0	0,6	0	1,0	0,6	AD	0,3	0	0	-0,4	0	0
30	0	0	0,5	1,0	0	0,5	AB	0	0,2	0	0	0,8	0

Таблица 4

Данные к заданию 2

Группа	Плоскость действия пары сил – пластина	M	P1	P2	F			
1	1	-3	2	1	4	60˚	30˚	90˚
2	2	2	3	2	6	90˚	45˚	45˚
3	1	4	3	1	4	30˚	90˚	60˚
4	2	-2	4	3	5	45˚	45˚	90˚
5	1	-4	2	3	6	90˚	60˚	30˚
6	2	3	3	2	5	60˚	90˚	30˚

.

Составим уравнения равновесия пространственной системы сил, приложенной к составной пластине:

,

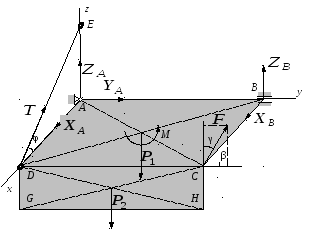
Рис. 8

,

,

,

,

,

где .

Решая поочередно эти уравнения, определим, кН:

;

;

;

;

;

.

Ответ представим таблицей:

					T
-3,854 кН	2 кН	2,464 кН	4,471 кН	-0,464 кН	0,817 кН

Расчетно-графическая работа по кинематике

Простейшие движения твердого тела

Приступая к выполнению заданий по кинематике, необходимо вспомнить простейшие виды движения твердого тела.

Поступательным движением твердого теланазывается такое его движение, при котором любая прямая, жестко связанная с этим телом, за все время движения остается параллельной своему первоначальному положению. При поступательном движении все точки твердого тела описывают одинаковые траектории и в каждый момент времени имеют равные скорости и равные ускорения.

Вращением твердого тела вокруг неподвижной осиназывается такое его движение, при котором две точки этого тела за все время движения остаются неподвижными. При вращательном движении скорость любой точки твердого тела перпендикулярна радиусуR окружности, по которой движется эта точка и направлена в сторону поворота твердого тела, а ее модуль равен произведению модуля угловой скорости |ω|твердого тела на этот радиус:

v=|ω|R.

Ускорение точки вращающегося твердого тела состоит из двух составляющих:

Касательная составляющая ускорения направлена так же, как и скорость этой точки, если вращение ускоренное, либо в противоположную сторону, если вращение замедленное. Модуль этой составляющей

Нормальная (центростремительная) составляющая ускорения направлена к центру окружности, по которой движется точка, а ее модуль

Плоскопараллельным (плоским) движением твердого теланазывается такое движение твердого тела, при котором все его точки движутся в плоскостях, параллельных одной неподвижной плоскости. Скорость любой точкиВ плоской фигуры определяется по формуле

,

где - скорость полюса; - скорость точки, которая получается при вращении плоской фигуры вокруг этого полюса.

Для плоского, как и для любого другого движения твердого тела, справедлива теорема о проекциях скоростей:проекции скоростей точек твердого тела, лежащих на одной прямой, на эту прямую равны.

При нахождении скоростей различных точек плоской фигуры весьма удобно воспользоваться понятием мгновенного центра скоростей. Мгновенным центром скоростей (МЦС)называется точка плоской фигуры либо точка плоскости, жестко связанной с этой плоской фигурой, скорость которой в данный момент времени равна нулю.

Рассмотрим основные способы нахождения МЦС:

• в некоторых случаях удается сразу найти точку плоской фигуры, скорость которой в данный момент времени равна нулю. Эта точка и будет являться мгновенным центром скоростей. Например, при качении без проскальзывания круглого цилиндра по неподвижной плоскости точка Pсоприкосновения этих тел является МЦС (рис. 9,а);

• если известны направления скоростей двух точек плоской фигуры, то МЦС находится в точке пересечения перпендикуляров, проведенных в этих точках к направлениям скоростей (рис. 9, б);

• в случае, когда точки лежат на общем перпендикуляре к направлениям их скоростей, МЦС находится на пересечении этого перпендикуляра и прямой, проходящей через концы векторов скоростей (рис. 9, в,г);

• если, кроме того, эти скорости равны по модулю и направлению, то МЦС не существует. Скорости всех точек плоской фигуры в этот момент времени геометрически равны (рис. 9, д);

• если скорости двух точек плоской фигуры параллельны и не лежат на общем перпендикуляре к скоростям, то они равны, МЦС отсутствует, а скорости всех точек этой фигуры также равны (рис. 9, е).

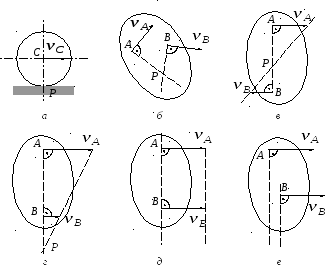
Рис. 9.

Отметим свойства скоростей точек плоской фигуры, связанные с понятием МЦС:

• скорости точек плоской фигуры перпендикулярны отрезкам, соединяющим эти точки с МЦС, и направлены в сторону поворота плоской фигуры;

• модули скоростей точек плоской фигуры прямо пропорциональны дли-

нам отрезков, соединяющих эти точки с МЦС, т.е.

v_A=AP |ω|, v_B=BP |ω|, v_C=CP |ω| ….

Ускорения точек плоской фигуры определяются при помощи теоремы

,

где – ускорение полюса; и – касательная и нормальная составляющие ускорения при вращении плоской фигуры вокруг полюса.